Visual Localization via Deep Learning
[deep-learning camera-estimation visual-localization 3d Visual localization aims to estimate the localization, which is usually the the coordinate (orientation and localization) in the world coordindately, given one or multiple images.
The camera model can be simplely written as $p_i = C h y_i$, where $p_i$ is the image coordinate, $C$ is the camera intrinsic matrix, $h$ is the camera post and $y_i$ is the real world coordinate. The camera pose $h$ can be defined as: \(p \in \mathbb{SE}(3) = \{\begin{pmatrix}R & t\\0&1\end{pmatrix}\lvert R\in\mathbb{SO}(3),t\in\mathbb{R}^3\}\) \(R\in\mathbb{SO}(3)=\{R\in\mathbb{R}^{3\times 3}\lvert RR^T = I,det(R)=1\}\)
The methods can be roughly divided into two groups:
- feature based approaches, which perform feature mapping of the input images to the model, and compute the coordinate based on the mapping;
- learning based approaches, which aims to compute the coordinate directly from the input image(s).
The contents of this note will mainly focus on learning based approaches.
Introduction
Most deep learning based visual localization approaches take the following architecture. However, there are different choices on the CNN backbones (e.g., VGG16, GoogLeNet, ResNet) and loss functions (Geometric loss functions for camera pose regression with deep learning).
The rotation matrix can also be written as an unit Quanterion: \(R\to q=(c,\theta,\rho,\eta)\in\lVert q\rVert=1\)
The lost function should be applied to both $R$ and $t$. For $t$ the choise is simpler, we could use $\ell(t,t^)=\lVert t - t^\rVert$. But for $R$, it is much more difficult:
- Angular distance: $\ell(R,R^)=\lVert log(R^R^T)\rVert$
- Quaternion Distance: $\ell(q,q^)=\lVert q - q^\rVert$
- Log Quaternion Distance: $\ell(R,R^)=\lVert log(R^) - log(R^T)\rVert$
There are different choices on combining the loss for $R$ and $t$:
- Implicit/Metric: $\ell(R, t) = \ell(R) + \ell(t)\ or\ max(\ell(R), \ell(t)$
- Hand-Tuned: $\ell(R, t) = \ell(R) + \beta\ell(t)$
- Self-tuned: $\ell(R, t) = \ell(R)e^{-s_R} + s_R + \ell(t)*e^{-s_t} + s_t$
- reprojection error: $\ell(R, t) = \lVert\Pi_{R,t}(v)-\Pi_{R^,t^}(v)\rVert$
PoseNet
Posenet: A convolutional network for real-time 6-dof camera relocalization
PoseNet is the earliest work which tries to use convolution neural network to solve the camera post estimation problem. It learns to regression the input RGB image ($224\times224$) into a 6-DOF camera pose. Especially, the rotation is represented by Quanterion, where the loss function is $\ell(q, t) = \lvert t-t^\rvert_2 + \beta \lvert \frac{q}{\lvert q \rvert_2} - q^ \rvert_2$, where $t^$ and $q^$ is the ground truth of the camera location and orientation accordingly. For backbone, GoogleNet is used. The other contribution of the paper is to propose to use structure from motion to generate the groud truth camera post for the training data.

DSAC
DSAC -Differentiable RANSAC for Camera Localization Learning Less is More – 6D Camera Localization via 3D Surface Regression
Random sample consensus (RANSAC) is widely used in many vision tasks. It typically takes the following steps:
- generate a pool of hypothese
- score each hypothese, e.g., via consensus of number of inliners
- select the best hypothese
- refine hypothese
However, RANSAC is not differentiable, which limits its application in many learning based apporach. In DASC, a differeniable RANSAC is proposed, by modifiying the step select the best hypothese:
- $\hat{h} = \sum_j{\frac{e^{s_j}h_j}{\sum_i{e^{s_i}h_i}}}$
- $\hat{h} = h_j \sim \sum_j{\frac{e^{s_j}h_j}{\sum_i{e^{s_i}h_i}}}$
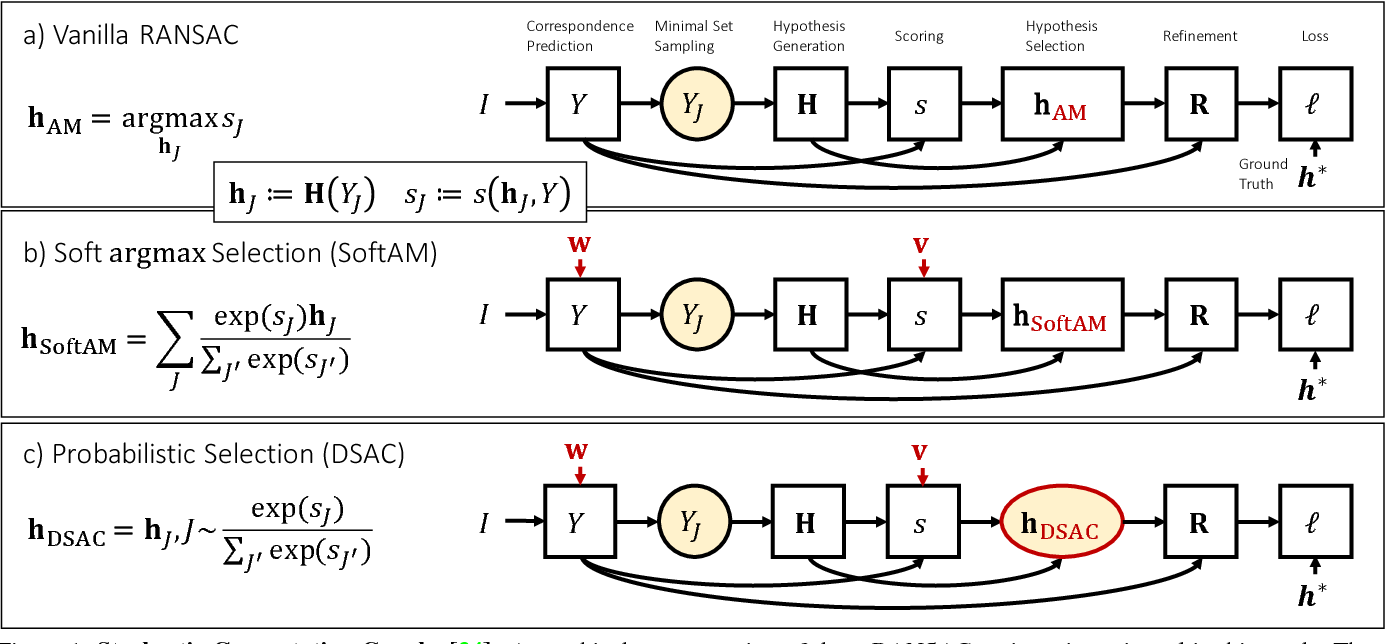
The proposed DSAC method is applied in camera post estimation problem, where a CNN is used to generate the hypothese given a $42\times42$ patch (with $40\times40$ patches per image) and the other CNN us used to score the hypothese. Those two CNNs are learned jointly and end-to-end.

DSAC+ method addresses the problem that the scoring CNN used in DSAC is prone to overfit/collapse. As a result, a inliner count is used instead. To make the count differentiable, sigmoid function replaces the step function. The input is $640\times 480$ image and output is $80\times60$ scene coordinate.
Spatial LSTM
Spatial LSTM claims using a $2048$-dim output of CNN to regress for pose in PostNet is prone to overfit and affects the accuracy. To address this problem, Spatial LSTM proposes to use four LSTMs to extract structure information from $2048$-dim CNN output in four directions, which each reduce the dimension to $32$.
To my opinion, the benefits of using four LSTM to extract structure information in four directions is not very clear.

VidLoc
VidLoc: A Deep Spatio-Temporal Model for 6-DoF Video-Clip Relocalization
VidLoc proposes to use bidirectionary LSTM to explore the temporal information when computating the camera pose sequence from video. A CNN (similar as PoseNet) is used to extract feature from the image and then feed into LSTM.

MapNet
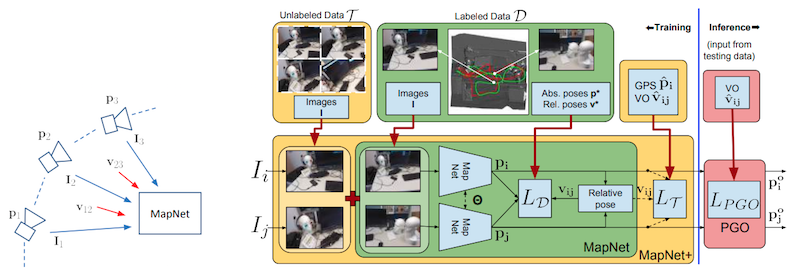
MapNet improves PoseNet from the following aspects:
- Log Quaternion Distance: $\ell(R,R^)=\lVert log(R^) - log(R^T)\rVert$ is used for rotation angle;
- pairwise constraint is introduced for the relative pose between two frames, where the ground truth relative pose can be obtained via visual odometry or sensor (e.g., gyro)
- unlabled data is introduced, where pairwise constraint is applied;
- to further smooth the trajectory and improve accuracy, a global pose optimization (GPO) is applied for post processing for a window of $k$ frames: \(L_{PGO}(\{p_i\}_{i=1}^T)=\sum_i{l(p_i^*,p_i)}+\sum_{i\neq j}{h(v_{i,j},v_{i,j}^*)}\)
- For backbone ResNet is used instead of GoogLeNet in PoseNet.
VLocNet
Deep Auxiliary Learning for Visual Localization and Odometry VLocNet++: Deep Multitask Learning for Semantic Visual Localization and Odometry
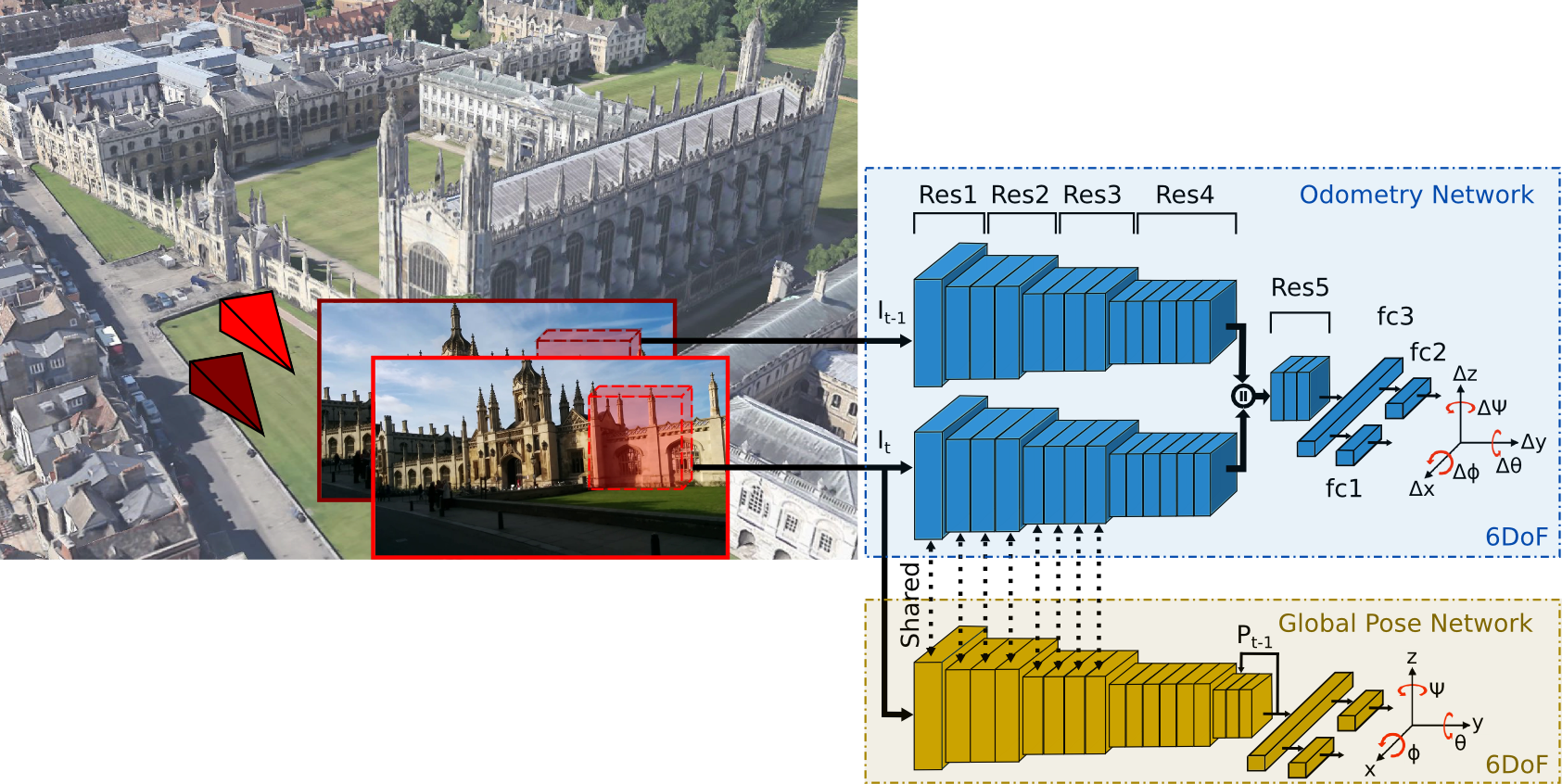
VLocNet improves PoseNet by adding a constraint on the relative pose for two adjacent frames (visual odometry), which is referred as auxillary learning (multi-task learning), similar as VidLoc. ResNet-50 is used as the backbone, and Siamese network on ResNet-50 is used for the constraint on relative pose.
VLocNet++ approach further improves this multi-task learning idea by combining the semantic segmentation task into the pose estimation and visual odometry task.
NetVLAD
NetVLAD: CNN architecture for weakly supervised place recognition

NetVLAD aims to learn a visual descriptor for place recognition. NetVLAD uses CNN as feature extractor and proposes to use Vector of Locally Aggregated Descriptors (VLAD) to replace existing pooling methods. VLAD is similar to the clustering:
\[V(j,k)=\sum_i{\frac{e^{-\alpha\lvert x_i^j - c_k^j \rvert_2^2}}{\sum_l{e^{-\alpha\lvert x_i^j - c_k^j \rvert_2^2}}}(x_i^j - c_k^j)}\]where $x_i^j$ is the $j_{th}$ dimension of $i_{th}$ feature.
In order to have sufficient training data, NetVLAD proposes the utilize the week label in Google street time machine data, which provides many panonama images associated with GPS location. NetVLAD assumes that the images with close GPS is likely to be similar to each other (potential positive, though we don’t know which one) and images with far GPS is unlikely to be similar to each other (hard negative), that means: \(\min_i{d(q, p_i)} +\epsilon <= d(q, p_j)\ \forall j\) , which naturally fits to hinge loss: \(L=\sum_j{max(0, \min_i{d(q, p_i)} +\epsilon - d(q, p_j))}\)
MapNet
MapNet: An Allocentric Spatial Memory for Mapping Environments
MapNet proposes to use the recurrent network to remember places visited in the past, as well as to re-localize itself with respect to those, which is updated incrementally using camera observations. In order to localize, these ground-projected camera features are matched against all possible rotations and locations (2D, since z is known).

