Network Compression
[bit-compression seperable-filter mobilenet xception low-rank-approximation deep-learning squeezenet network-pruning quantization sparsity The trained network is typically too large to run efficiently on mobile device. For example, VGG16 used for image classification has more 130 Million parameter (about 600 MB on model size) and requires about 31 billion operations to classify an image, which is way to expensive to be done on mobile.
We need to shrink the network, which will be introduced below.
Network Prunning
This method tries to reduce the size of network, which could be
- removing some layers: ThiNet
- removing some channels: Channel Pruning, Discrimination-aware Channel Pruning
- removing single filters: Deep Compression, Sparse-Winograd, Neuron Pruning

Distill the knowledge in neural network
This method is trying to train a small network to mimick a large network.

Examples include SqueezeNet, MobileNet
Low rank approximation
Major of the computation in neural network training and inference is matrix production. For matrix production, \(A \times B\), if $A \in R^{m \times n}$ can be written as product of A1 and A2 where $A_1\in R^{m \times k}$ and $A_2\in R^{k \times n}$ with $k \lt m, n$, then we can write $A \times B = A_1 \times (A_2 \times B)$. The computational can be reduced by a factor of $\frac{2 \times k}{m + n}$
Bit Quantization
It has been shown in experiment that, for inference, 32 bit single precision float is not required, 16 bit or even 8 bit fixed point is sufficient. Some experiment even pushes to 4 bit or just 1 bit. Note, the mapping from 32 bit to 8 bit may not be linear.
Examples:
- 1 bit: XNORnet, ABCnet with Multiple Binary Bases, Bin-net with High-Order Residual Quantization, Bi-Real Net
- 2 bit: Ternary weight networks, Trained Ternary Quantization
- 8 bit: Learning Symmetric Quantization
- 8 bit int: TensorFlow-lite, TensorRT
- nonlinear: Intel INQ, log-net, CNNPack
Sparsity
The multiplication of a number to zero is always zero. If the parameter of the network contains a lot of zero, then we can save a lot of multiplication operation. We can set the parameter which are small enough to zero and roughly maintain the performance of the network. Sparsity constraint can be also added during the training stage to encourage the trainied network to be sparse.
Separable Filter
A seperate filter means the 2D convolution can be done as a sequence of two 1D convolution: \(x * f = (x * f_x) * f_y\). The cost ratio would be: \(\dfrac{B}{A} = \dfrac{ H * W * h_1 * w_1 * 1 * c_1 + H_m * W_m * 1 * 1 * c_1 * c_2}{H * W * h1 * w1 * c_1 * c_2}= \dfrac{1}{c_2} + \dfrac{1}{h_1 * w_1}\)
Examples
SqueezeNet
SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and < 0.5MB model size
It bases on three technique:
- uses 1x1 convolution instead of 3x3 one;
- reduce the input channel number for 3x3 convolution;
- avoid stride in convolution layer

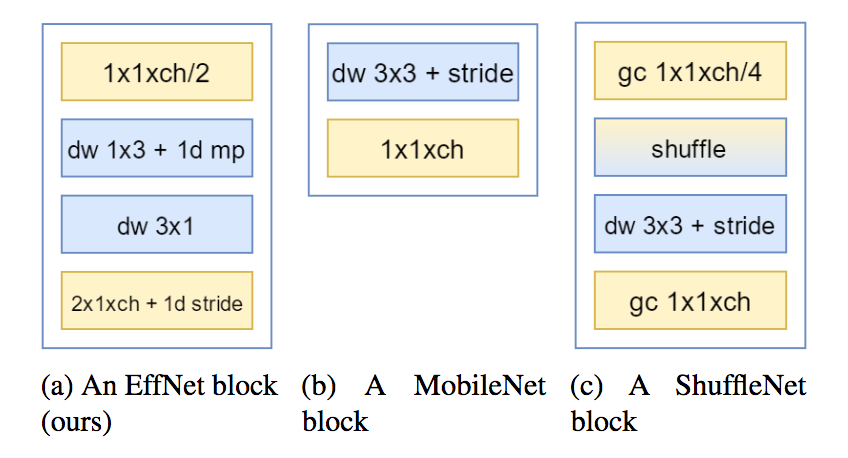
MobileNets
MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications
IT bases on uses depth wise convolution and 1x1 convolution

MobileNets V2
Inverted Residuals and Linear Bottlenecks: Mobile Networks for Classification, Detection and Segmentation
Xception
Xception: Deep Learning with Depthwise Separable Convolutions
It is an optimization over Inception V3 via using depthwise separable convolution.
ShuffleNet-v1
ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices
It is similar to mobile-net.

ShuffleNet-v2
ShuffleNet V2: Practical Guidelines for Ecient CNN Architecture Design

EffNet
EffNet: An Efficient Structure for Convolutional Neural Networks
EffNet uses spatial separable convolutions. It is very similar to MobileNet’s depthwise separable convolutions. The separable depthwise convolution is the rectangle colored in blue for EffNet block. It is made of depthwise convolution with a line kernel (1x3), followed by a separable pooling, and finished by a depthwise convolution with a column kernel (3x1).