Different Types of Convolutions in Deep Learning
[depthwise-convolution dilated-convolution transposed-convolution pointwise-convolution convolutions separable-convolution deep-learning grouped-convolution Besides the convolution operator we already found in AlexNet or VGG16, there are few variations, which will be introduced below. The content of this article is based on reading of An Introduction to different Types of Convolutions in Deep Learning
Convolutions
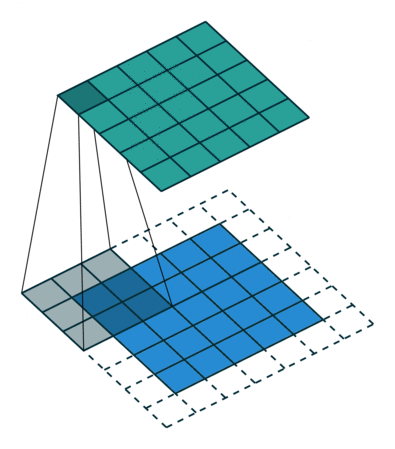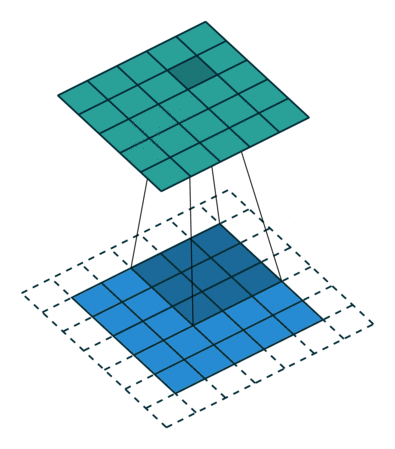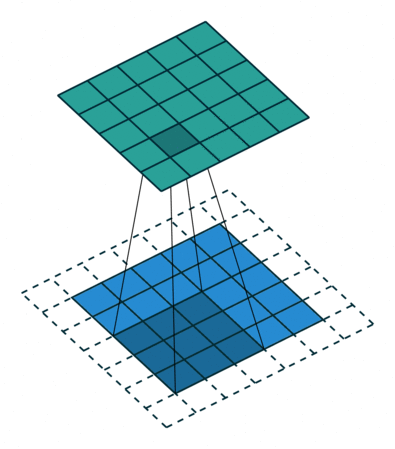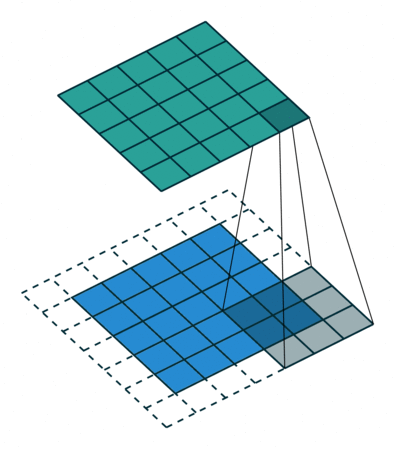The convolution can be described the image above. It will have the following parameters:
- Kernel Size: The kernel size defines the field of view of the convolution. A common choice for 2D is 3 — that is 3x3 pixels.
- Stride: The stride defines the step size of the kernel when traversing the image. While its default is usually 1, we can use a stride of 2 for downsampling an image similar to MaxPooling.
- Padding: The padding defines how the border of a sample is handled. A (half) padded convolution will keep the spatial output dimensions equal to the input, whereas unpadded convolutions will crop away some of the borders if the kernel is larger than 1.
- Input & Output Channels: A convolutional layer takes a certain number of input channels (I) and calculates a specific number of output channels (O). The needed parameters for such a layer can be calculated by IOK, where K equals the number of values in the kernel.
Dilated Convolutions
Dilated Convolutions or atrous convolutions, which uses a lot in image segmentation, controls the field of view size by both kernel size and dilation rate–larger kernel size and higher dilation rate mean large field of view size for convolution. Compared with convolution above, atrous convolutions could use dilation rate > 1 to achieve the large field size while not require large kernel size, which means lower computation cost.
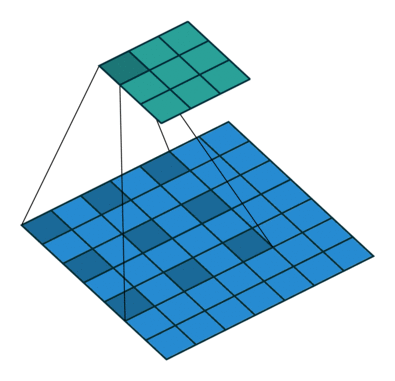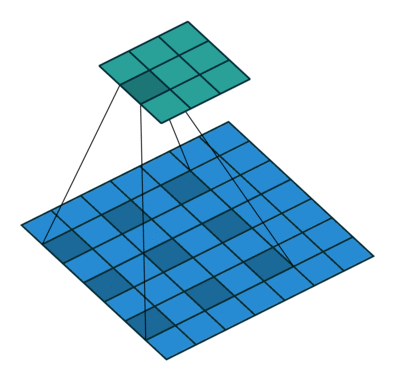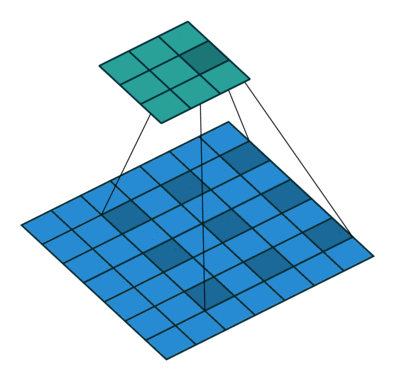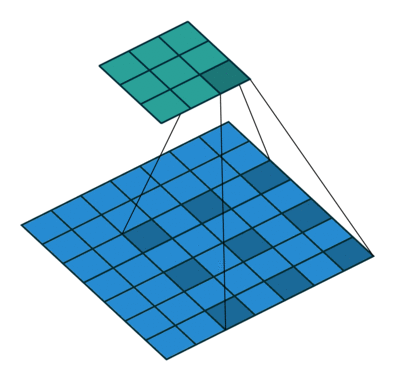
Transposed Convolutions
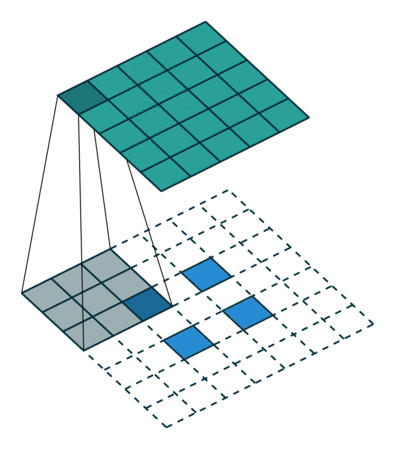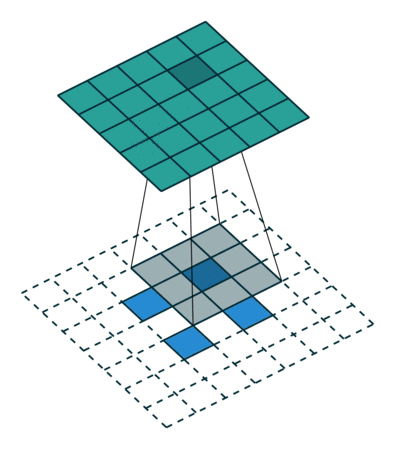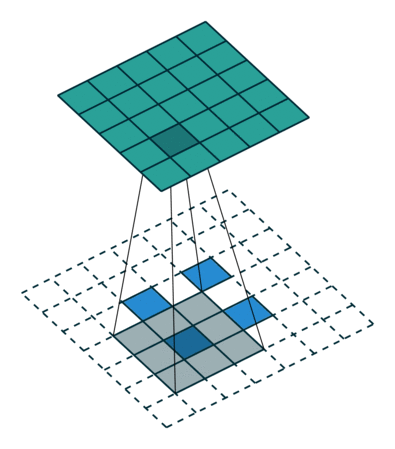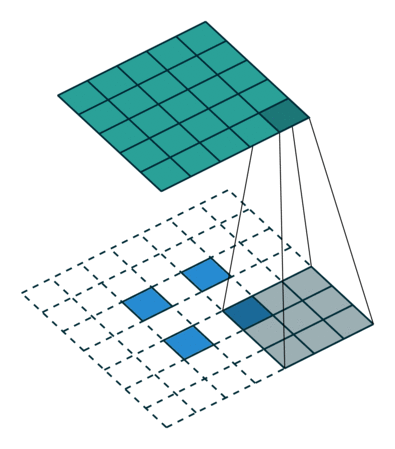
Transposed Convolutions or deconvolutions or fractionally strided convolutions can be viewed as reverse operation of convolutions. It merely reconstructs the spatial resolution from before and performs a convolution. This may not be the mathematical inverse
Separable Convolutions
Separable Convolutions means a 2D convolution can be decoupled as a sequence of two 1D convolution, one in row and the other one in column. The benfits is the reduction of computational cost, e.g., a separable convolutions will require 6 parameters instead of 9.
grouped convolution
Filter groups or grouped convolution was introduced in AlexNet mainily to address memory issue. Below is illustrated a convolutional layer with 2 filter groups, where each the filters in each filter group are convolved with only half the previous layer’s featuremaps. It works because filter relationships are sparse.
