Advancing Example Exploitation Can Alleviate Critical Challenges in Adversarial Training
[gairat mart teat accuracy sat gan fastat deep-learning robust grad-align This is my reading note for Advancing Example Exploitation Can Alleviate Critical Challenges in Adversarial Training. The paper proposes a simple method to improve performance of adversarial learning. It’s based on the observation that some samples has impacts to robustness but not accuracy; Vice verse. Thus it propose a method to adjust the weight of samples according.
Introduction
To address this issue, we provide a comprehensive summary of representative strategies focusing on exploiting examples within a unified framework. Furthermore, we investigate the role of examples in AT and find that examples which contribute primarily to accuracy or robustness are distinct. Based on this finding, we propose a novel example-exploitation idea that can further improve the performance of advanced AT methods. This new idea suggests that critical challenges in AT, such as the accuracy-robustness trade-off, robust overfitting, and catastrophic overfitting, can be alleviated simultaneously from an example-exploitation perspective. (p. 1)
AT is not without limitations and confronts critical challenges, including: (1) the trade-off between accuracy (classification success rate for original samples) and robustness (classification success rate for examples after adding adversarial perturbations), where improving one metric comes at the expense of the other [3]; (2) the phenomenon of robust overfitting (RO), which is characterized by a gradual decline in robustness during the later stage of training [6]; and (3) the occurrence of catastrophic overfitting (CO), which leads to a sudden drop in robustness after a particular epoch of training [7]. (p. 1)
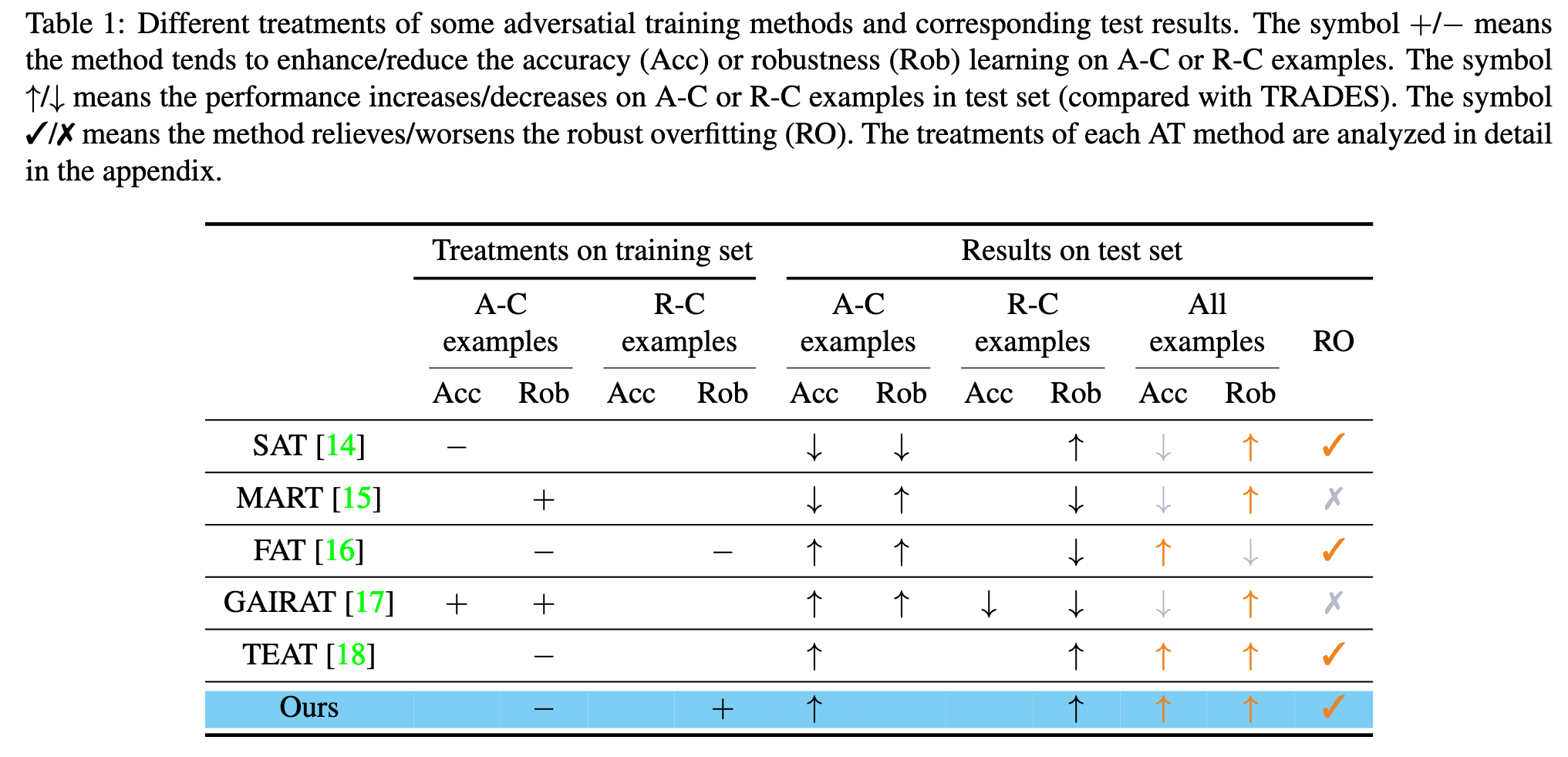
To prevent the model from overfitting erroneous features, SAT dynamically adjusts the one-hot label of each example in each training epoch [14]. MART prioritizes the impact of misclassified examples on model robustness by incorporating a misclassificationaware term into its objective function [15]. FAT assigns each example a different attack iteration to search for friendly adversarial examples that can improve model accuracy [16]. GAIRAT reweights the loss function for each example based on its geometry value, which approximates the distance from the example to the class boundary [17]. The recent work TEAT integrates the temporal ensembling approach to prevent excessive memorization of noisy adversarial examples [18]. Although these works offer various strategies for exploiting examples, their underlying insights are different and sometimes conflicting. For instance, MART focuses on examples that FAT aims to avoid. (p. 1)
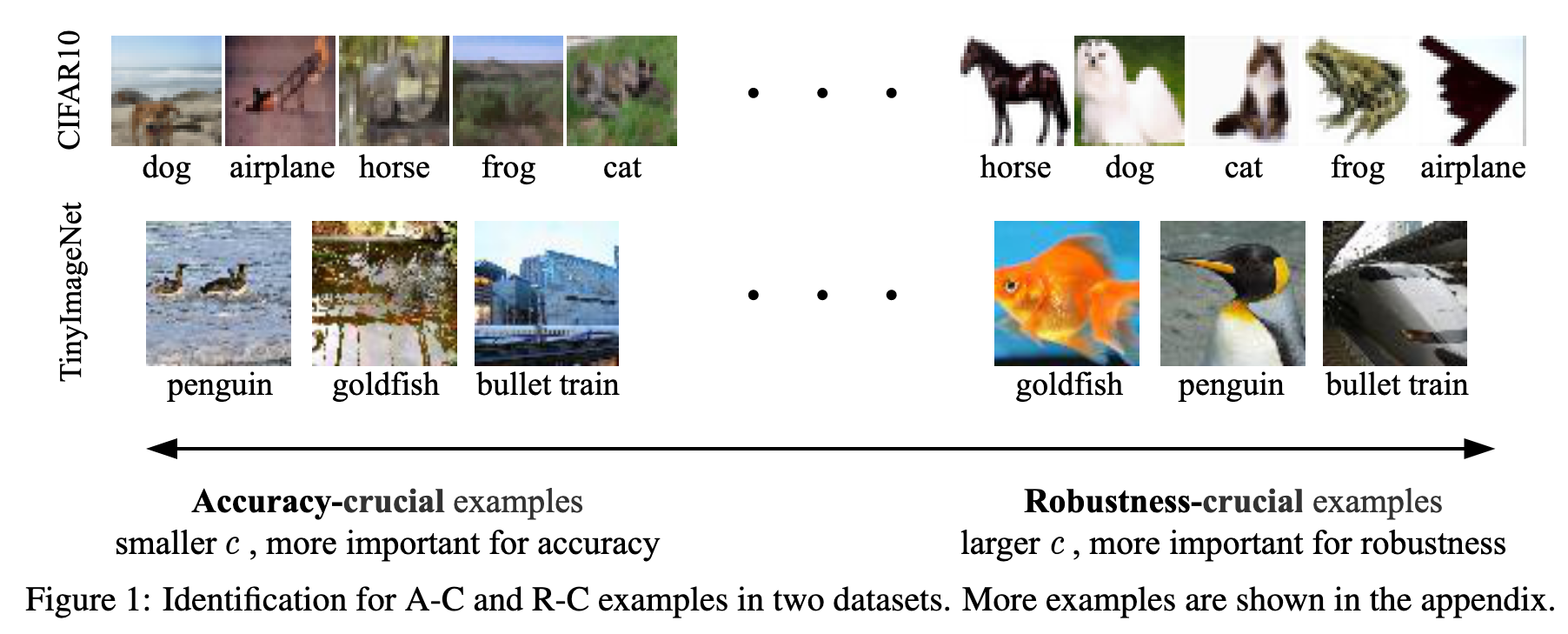
In this paper, we propose an unified framework to summarize the exploiting strategies used in representative works by dividing examples into two crucial parts: accuracycrucial (A-C) and robustness-crucial (R-C). Our investigation shows that A-C and R-C examples significantly contribute to accuracy and robustness, respectively, and the insights of existing example-exploitation research can be interpreted as treating A-C and R-C examples differently (p. 2)
Related work
According to [2], training a robust classification model can be formalized as the following min-max optimization problem: (p. 2)
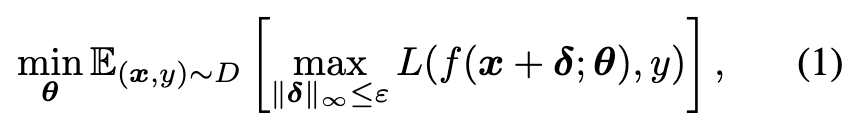
The inner maximization is approximated by generating adversarial perturbation δ through the attack in the training process. One popular method to generate δ is Projected Gradient Descent (PGD) [2], which performs a fixed number of gradient ascent iterations using a small step-size a: (p. 2)
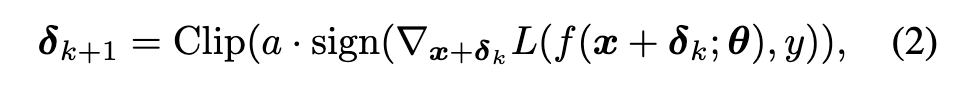
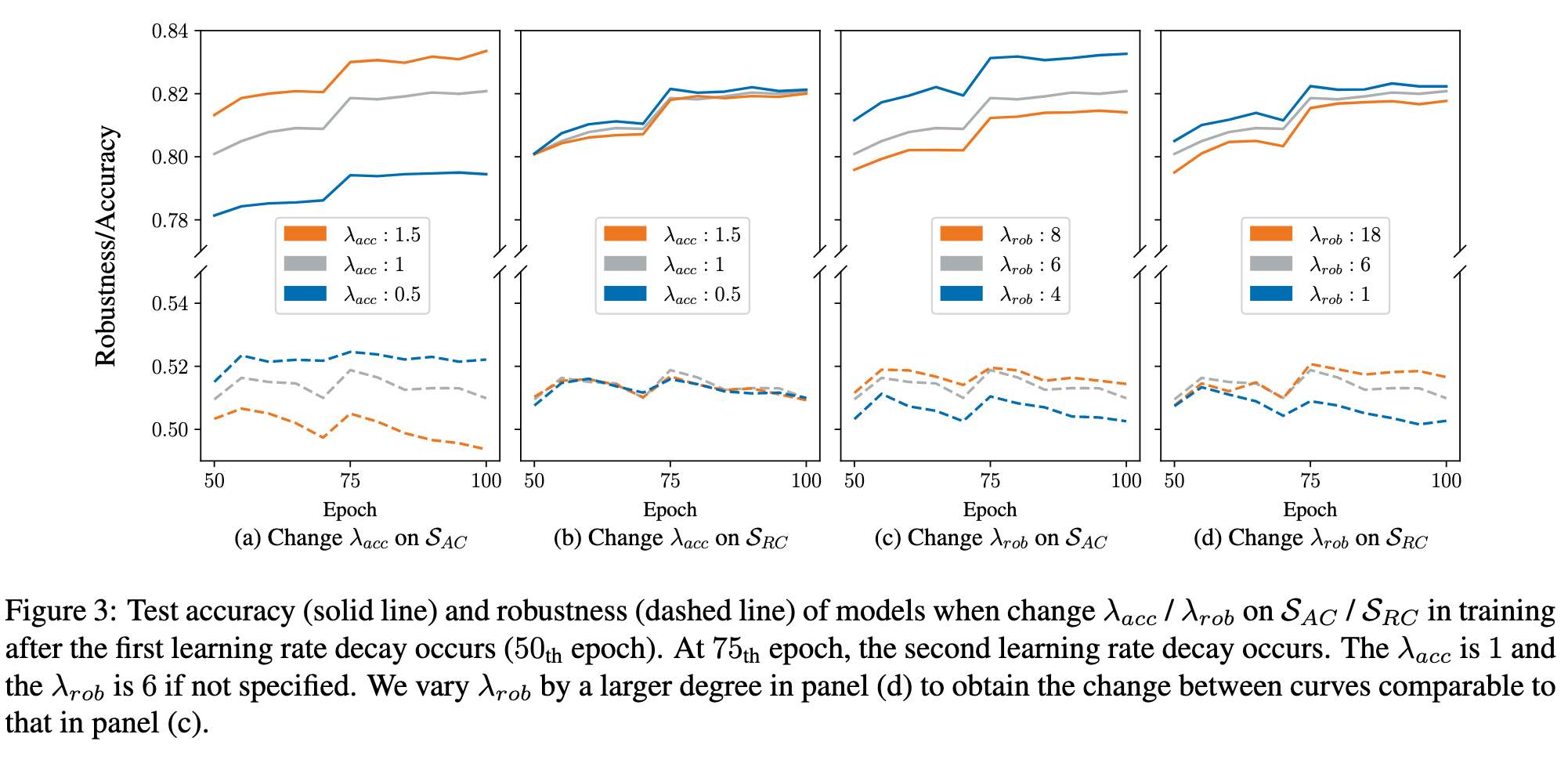
For balancing the them, TRADES [3] uses Kullback-Leibler divergence (KL) loss to implement L in Equation (2). The overall loss of TRADES is (p. 2)
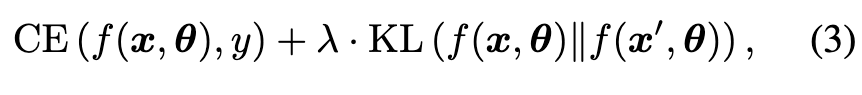
One iteration of gradient ascent with respect to the original examples x is performed to generate δ [19]: (p. 2)
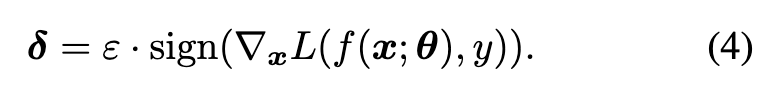
Roles of different examples
In this section, we introduce a new metric called ”robustness confidence” that can identify examples crucial to accuracy or robustness. We then use this metric to analyze representative adversarial training (AT) methods. (p. 2)
Robustness confidence of each example
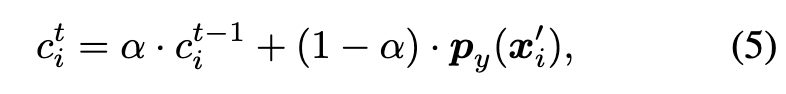
However, robustness confidence ci serves a distinct purpose: it quantifies the model’s ability to correctly classify adversarial examples x′ i generated from xi throughout the training process. A value of ci closer to 1 implies that the model can more easily fit the adversarial features around xi, whereas a value closer to 0 indicates that the model struggles to learn valid features from xi′, as py(x′ i) remains small in every epoch. (p. 3)
Accuracy/Robustness-crucial examples
Based on proposed robustness confidence c, we define two types of examples: accuracy-crucial (A-C) and robustness-crucial (R-C). An A-C example is characterized by having a small robustness confidence, while an R-C example has a large robustness confidence. (p. 3)
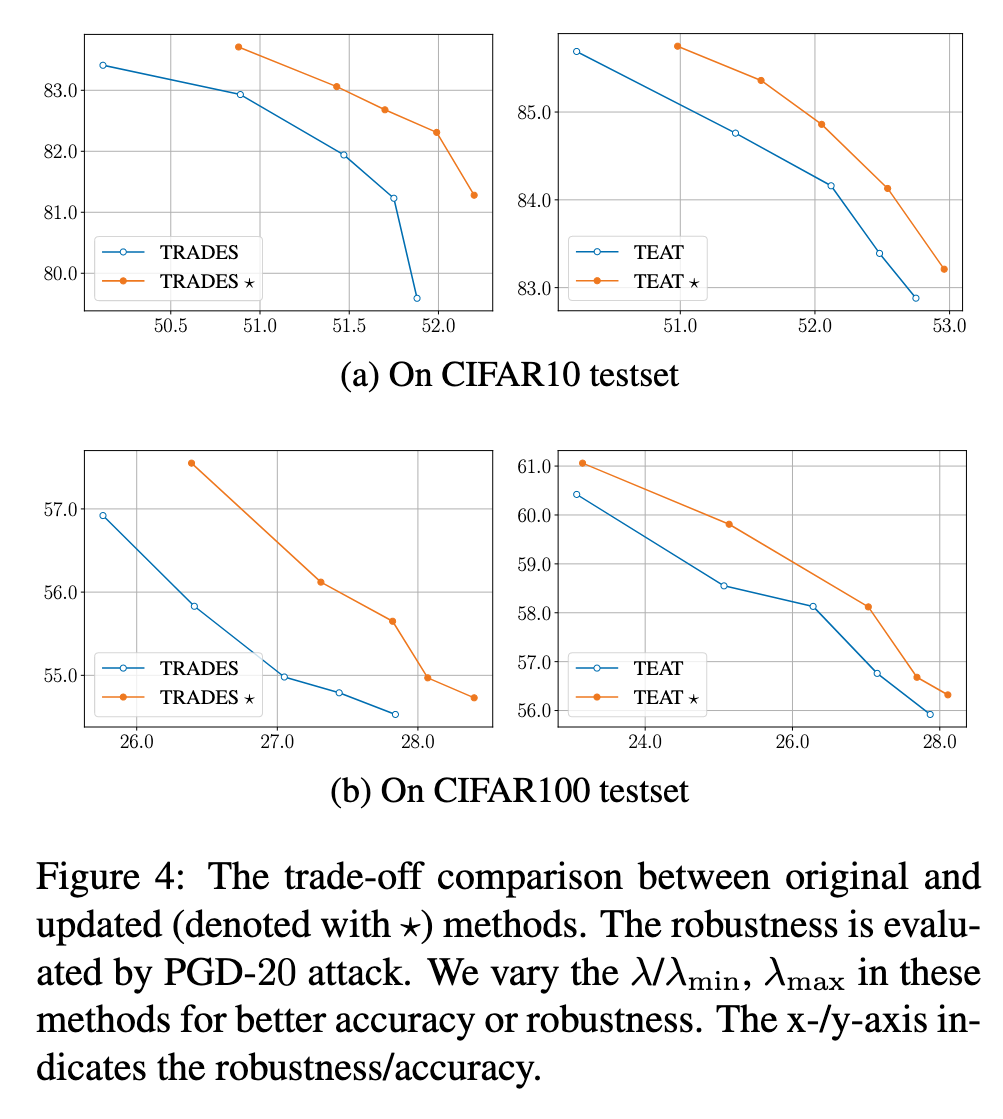
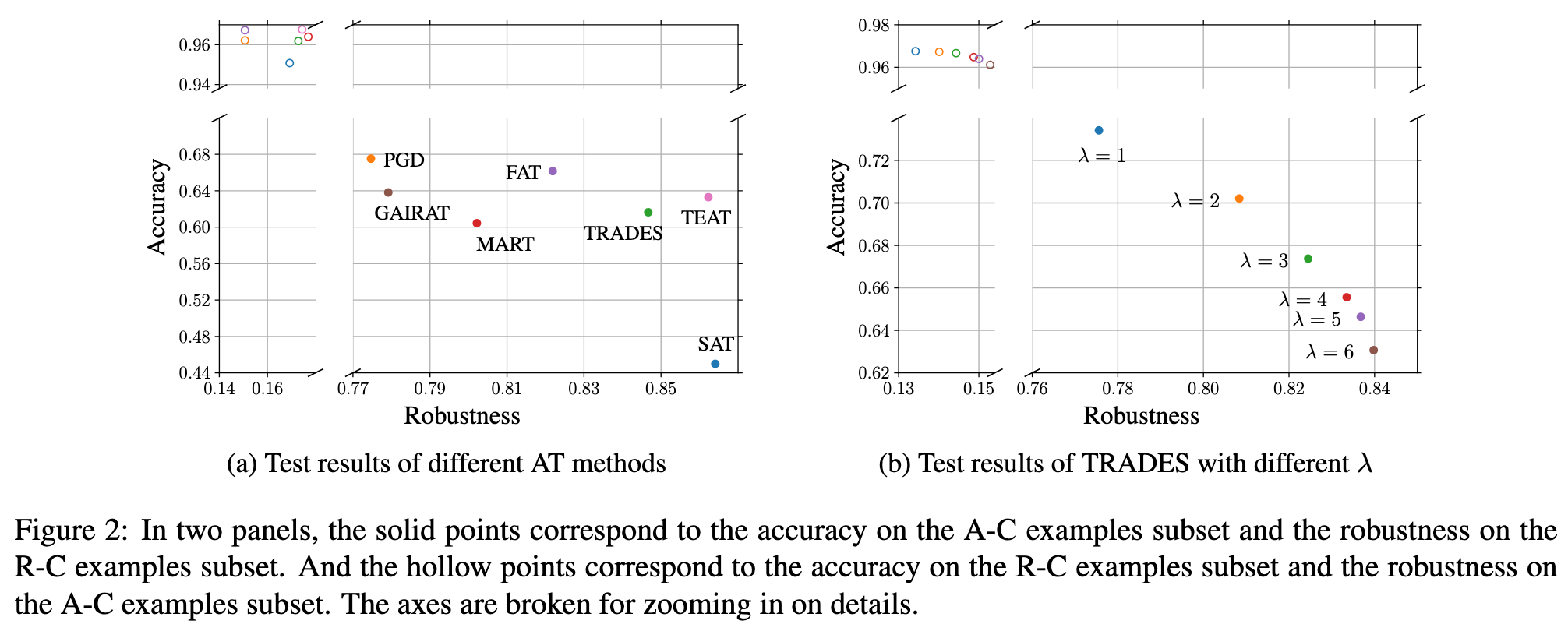
In Figure 2, we can observe the following: 1) The hollow points predominantly appear in the upper left corner, indicating that AT methods typically yield low robustness on AC examples and high accuracy on R-C examples. 2) Compared to the hollow points, the solid points display noticeable variability in the lower right region, suggesting that the performance differences among these AT methods mainly stem from their accuracy on A-C examples and robustness on R-C examples. 3) The results of the TRADES method provide a more intuitive rule: improving robustness on R-C examples can lead to a decrease in accuracy on A-C examples, and vice versa. These findings offer a novel insight into AT: To strengthen the effectiveness of adversarial training, it is important to emphasize accuracy on A-C examples and robustness on R-C examples. (p. 4)
Further exploitation on examples
Effect of A-C and R-C examples
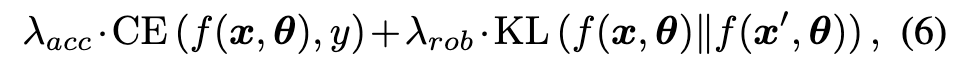
The main observations from the experiments, shown in Figure 3, are as follows: (p. 4)
This observation is linked to the discovery that in order to improve accuracy, the model needs to memorize A-C examples [28, 29, 30], which will come at the cost of reduced robustness [18]. Therefore, modifying the accuracy learning on A-C examples to enhance the model’s accuracy or robustness may not be appropriate for AT. changing λ_acc for R-C examples has less impact on test performance. (p. 5)
Specifically, when the robustness learning is reduced (represented by the blue lines), decreasing λ_rob on A-C examples (as shown in Figure 3c) results in more accuracy improvements with fewer sacrifices in robustness compared to decreasing λ_rob on R-C examples (as shown in Figure 3d). On the other hand, when enhancing the robustness learning (represented by the orange lines), increasing λ_rob on R-C examples (as shown in Figure 3d) leads to more improvements in robustness with less loss in accuracy compared to increasing λ_rob on A-C examples (as shown in Figure 3c). (p. 5)
Reasonableness of new treatment
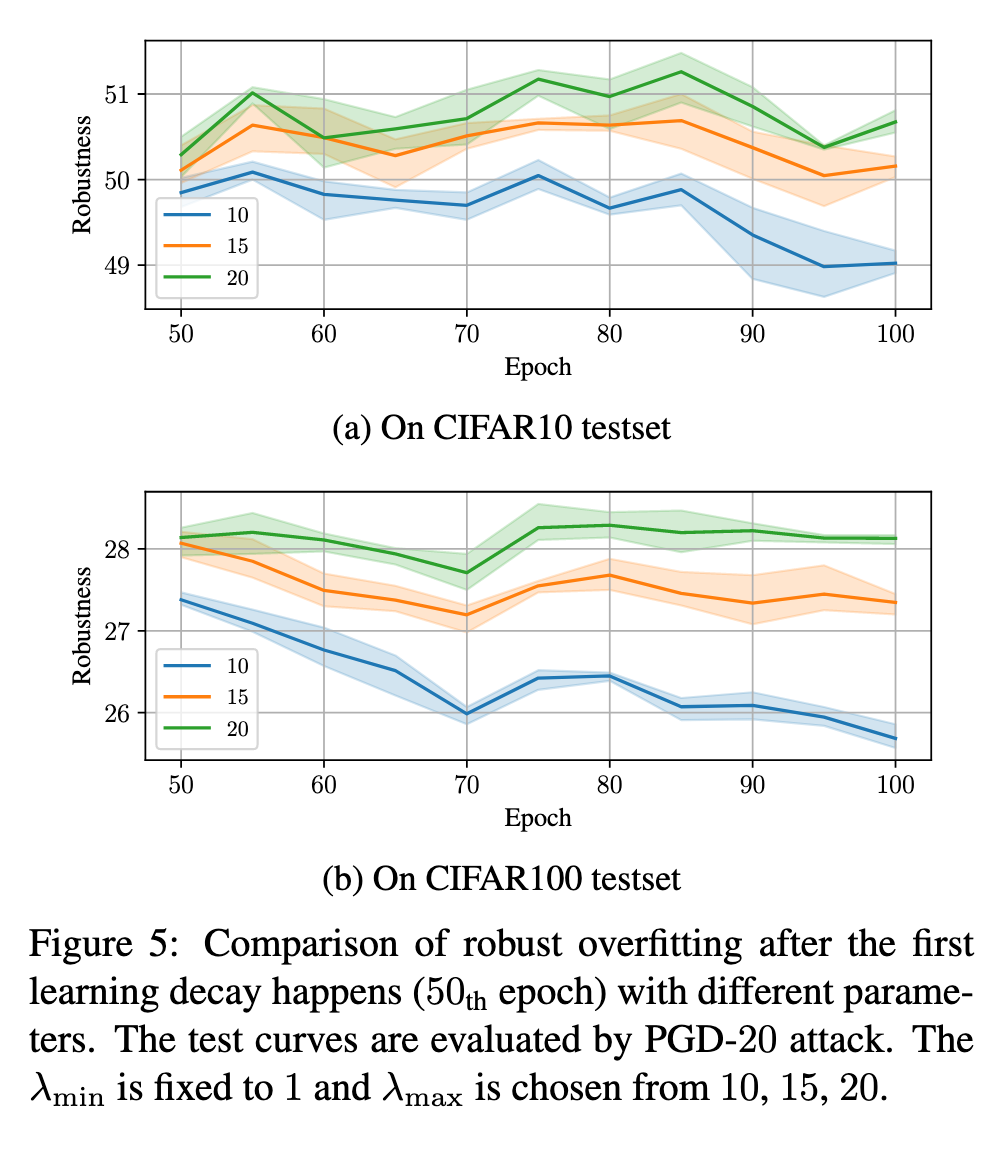
Based on our observations, we propose an appropriate treatment for examples in AT: reduce the robustness learning on A-C examples and enhance the robustness learning on R-C examples. (p. 5)
Application of new treatment
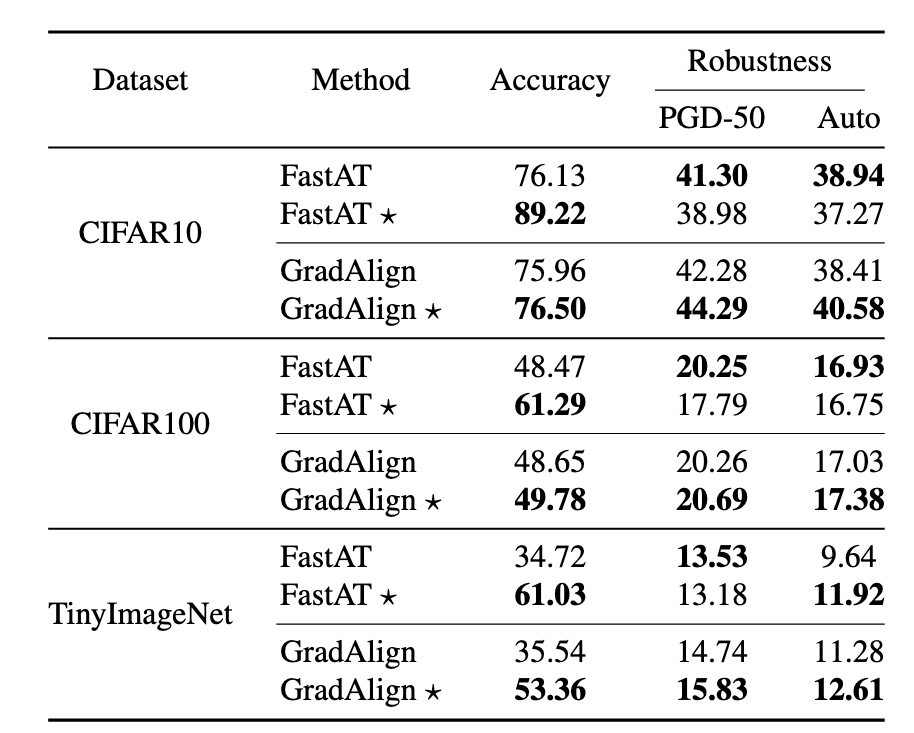
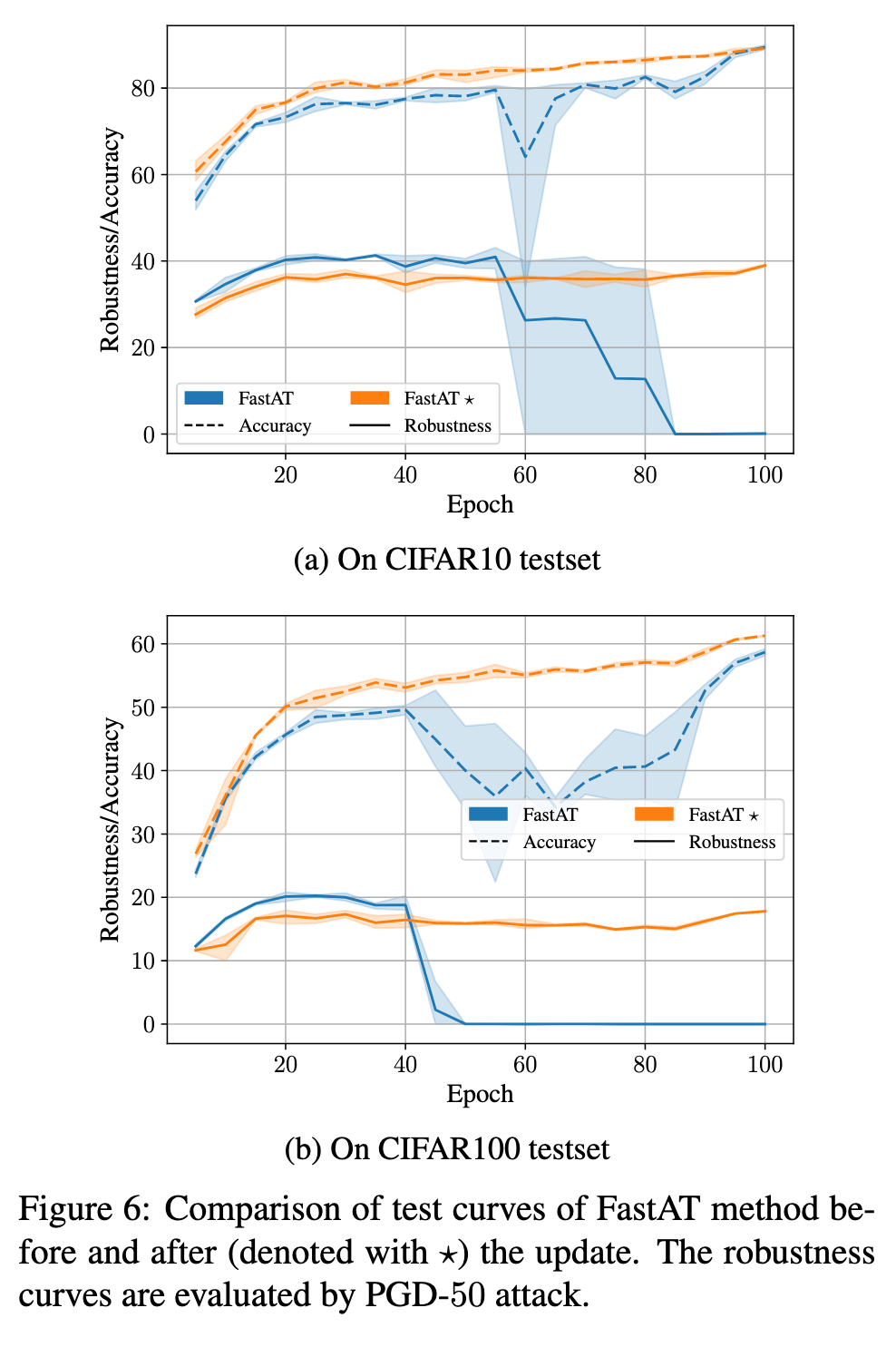
Specifically, we can replace a fixed hyper-parameter of existing methods with an adaptive one to adjust the degree of robustness learning for each example. (p. 5)
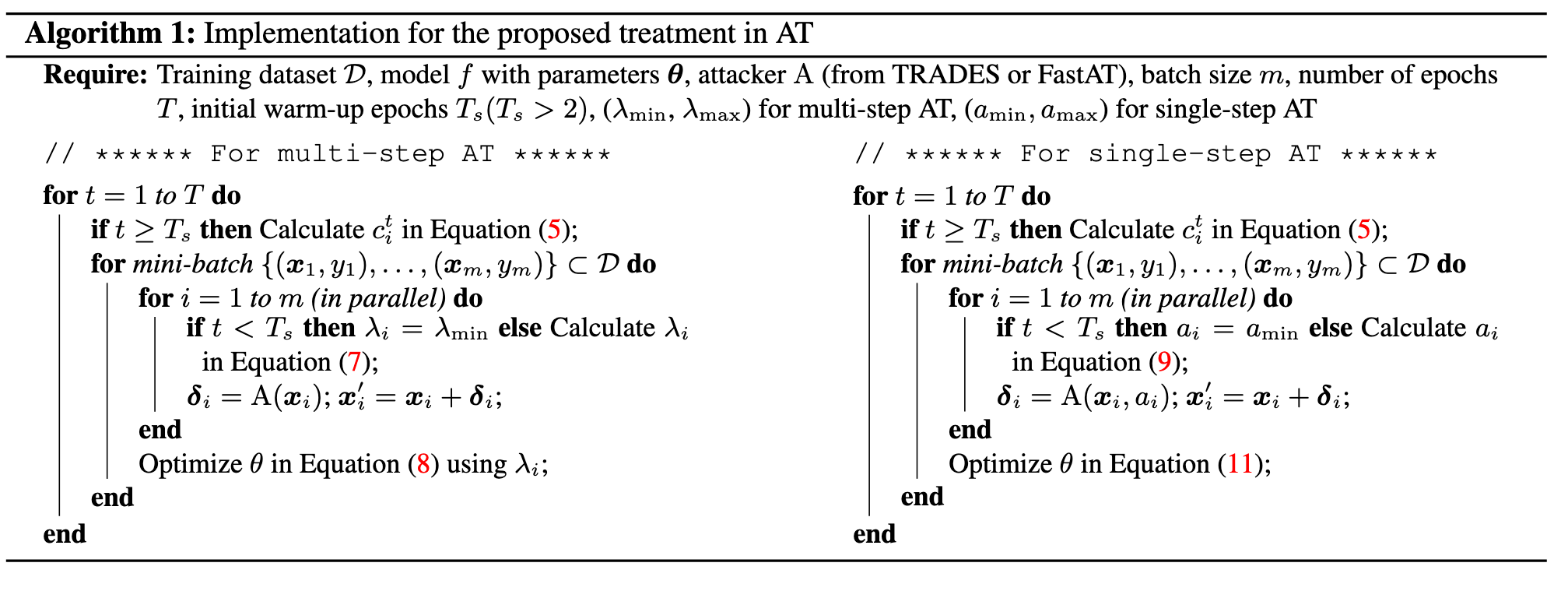
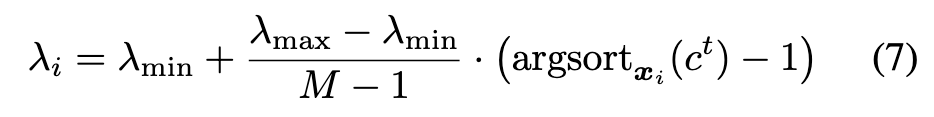
For single-step AT, considering FastAT method as a case, we use adaptive step-size ai instead the fixed one for each example xi to generate adversarial perturbation δi in training process: (p. 6)
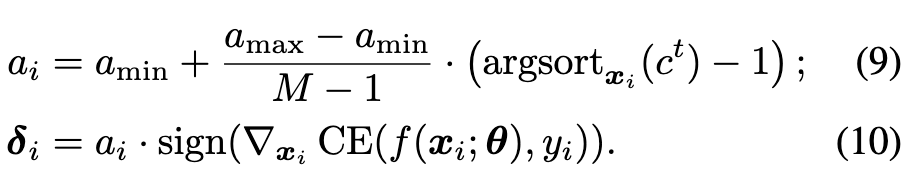
Advantages of new treatment