GANFIT Generative Adversarial Network Fitting for High Fidelity 3D Face Reconstruction
[3dmm identity progressive-gan single-image in-the-wild texture ganfit deep-learning arcface 3d This is my reading note for GANFIT: Generative Adversarial Network Fitting for High Fidelity 3D Face Reconstruction. The code is available in GANFit. GANFit reconstructs high quality texture and geometry from a single image with precise identity recovery. To do this, it utilizes GANs to train a very powerful generator of facial texture in UV space. Then, it revisits the original 3D Morphable Models (3DMMs) fitting approaches making use of non-linear optimization to find the optimal latent parameters that best reconstruct the test image but under a new perspective. It optimizes the parameters with the supervision of pretrained deep identity features through our end-to-end differentiable framework.
3D Morphable Model
3DMM uses linear model to represent both the texture and 3D shape of a face.
Texture
Traditionally 3DMMs use a UV map for representing texture. UV maps help us to assign 3D texture data into 2D planes with universal per-pixel alignment for all textures. A commonly used UV map is built by cylindrical unwrapping the mean shape into a 2D flat space formulation, which we use to create an RGB image IUV. Each vertex in the 3D space has a texture coordinate \(t_{coord}\) in the UV image plane in which the texture information is stored
Any test texture T is approximated as a linear combination of the mean texture \(m_t\) and a set of bases \(U_t\) as
\[T(P_t)=m_t+U_t P_t\]Shape
In order to represent both variations in terms of identity and expression, generally two linear models are used. The first is learned from facial scans displaying the neutral expression (i.e., representing identity variations) and the second is learned from displacement vectors. Then a shape S could be represented as:
\[S(P_{s,e})=m_{s,e}+U_{s,e}P_{s,e}\]where \(m_{s,e}\) is the mean shape, \(U_{s,e}=[U_s,U_e]\in\mathbb{R}^{3N\times n_{s,e}}\) is the shape basis and \(P_{s,e}=[P_s,P_e]\in\mathbb{R}^{n_{s,e}}\) is the shape parameter.
Fitting
3D face and texture reconstruction by fitting a 3DMM is performed by solving a non-linear energy based cost optimization problem that recovers a set of parameters.
\[\min_p\{\lVert I^0(p)-W(p)\rVert_2^2+\mbox{reg}(p_{s,e},p_t)\}\]where \(I^0\) is the input image, \(W(p)\) is the rendering process for the given parameter.
Proposed Method
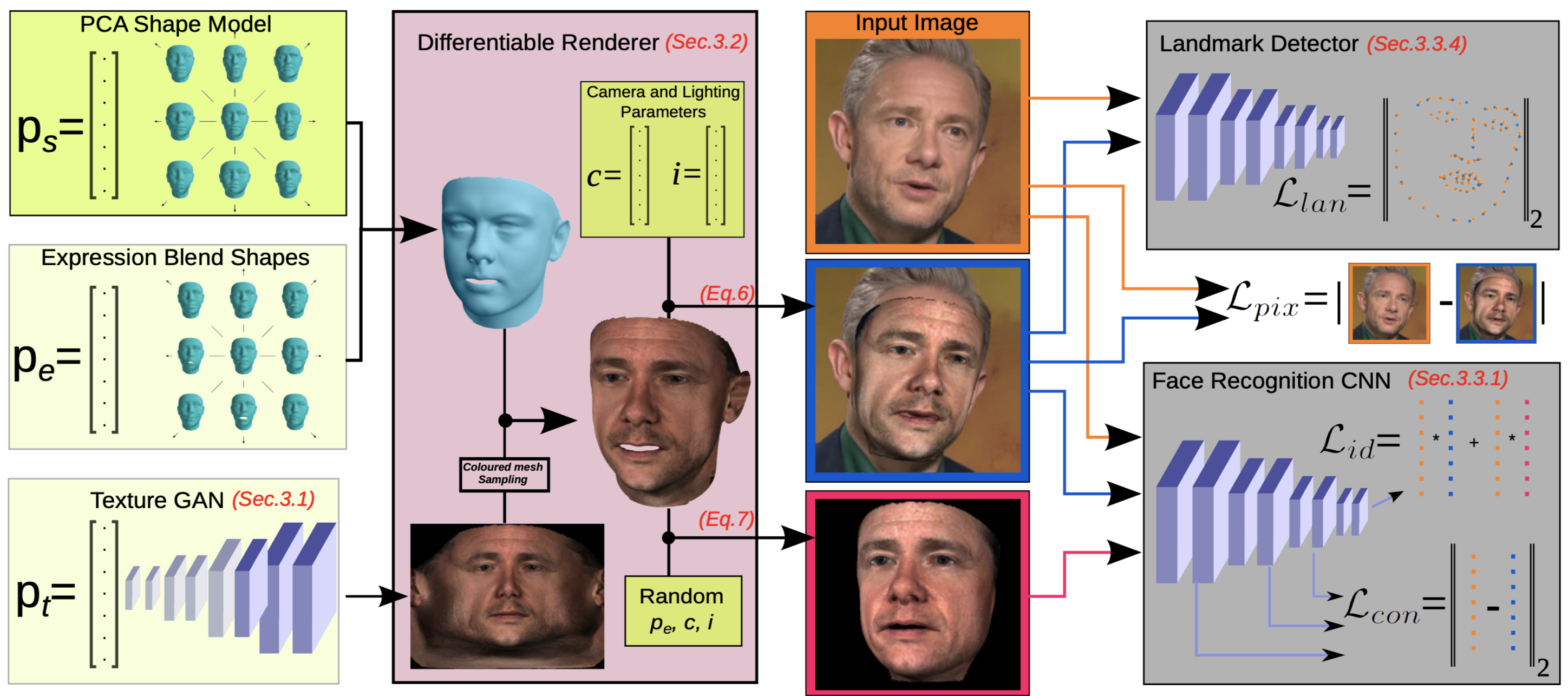
GAN to Estimate Texture
Linear model used by 3DMM is often unable to capture high frequency details and ends up having blurry textures due to its Gaussian nature. This becomes more apparent in texture modelling which is a key component in 3D reconstruction to preserve identity as well as photo-realism.
It is found GAN trained with UV representation of real textures with per pixel alignment avoids this problem and is able to generate realistic and coherent UVs. Thus GANFit trains a progressive growing GAN to model distribution of UV representations of 10,000 high resolution textures and use the trained generator network \(\mathcal{G}(p_t):\mathbb{R}^{512}\rightarrow \mathbb{R}^{H\times W\times C}\) as texture model that replaces 3DMM texture model
Differential Render
3D shape is based on the linear model of 3DMM. Given the shape parameter \(p_s,p_e\) and texture parameter \(P_t\), as well camera parameter \(p_c\) and lighting parameter \(p_l\), the image could be created via differential rendering:
\[I^R=\mathcal{R}(S(p_s,p_e),\mathcal{G}(p_t),p_c,p_l)\]In addition, another image is generated by randomizing all parameters except the identity parameter \(p_s\). This image should be labeled as the same identities as the previous image by face recognition model.
\[\hat{I}^R=\mathcal{R}(S(p_s,\hat{p}_e),\mathcal{G}(p_t),\hat{p}_c,\hat{p}_l)\]Cost Functions
The following cost functions are used:
- identity loss: the images generated by differential rendering should be labled to have the same identity as the input by face recognition model (ArcFace is used). Say \(F^i(I)\) is the output of face recognition model for image I at i-th layer, then this loss is written as \(\ell_{id}=1-\frac{F^n(I) F^n(I^R)}{\lVert F^n(I)\rVert_2\lVert F^n(I^R)\rVert_2}\) and \(\hat{\ell}_{id}=1-\frac{F^n(I) F^n(I^\hat{R})}{\lVert F^n(I)\rVert_2\lVert F^n(I^\hat{R})\rVert_2}\)
- content loss: output of intermediate layers of face recongition model is also compared to provide more pixel-level information, which is \(\ell_{con}=\sum_j^n\frac{\lVert F^j(I)-F^j(I^R)\rVert_2}{\mbox{sizeof}(F^j(I))}\)
- pixel loss: lighting conditions are optimized based on pixel value difference directly: \(\ell_{pix}=\lVert I^0-I^R\rVert_1\)
- landmark loss: eucliden distance between landmarks detected from input images and landmarks projected from fitted 3D shape is important to check the camera parameter as well as the 3D shape.
Implementation and Results
GANFit starts by optimizing shape, expression and camera parameters by landmark loss, then it simultaneously optimizes all of our parameters with gradient descent and backpropagation so as to minimize weighted combination of above loss terms.
For videos or images know to be from the same identities, the identity parameter \(p_s\) is averaged.
For all experiments, a given face image is aligned to our fixed template using 68 landmark locations detected by an hourglass 2D landmark detection. For the identity features, we employ ArcFace network’s pretrained models. For the generator network \(\mathcal{G}\), we train a progressive growing GAN with around 10,000 UV maps from [7] at the resolution of \(512\times512\). We use the Large Scale Face Model for 3DMM shape model with \(n_s\) = 158 and the expression model learned from 4DFAB database with \(n_e\) = 29.
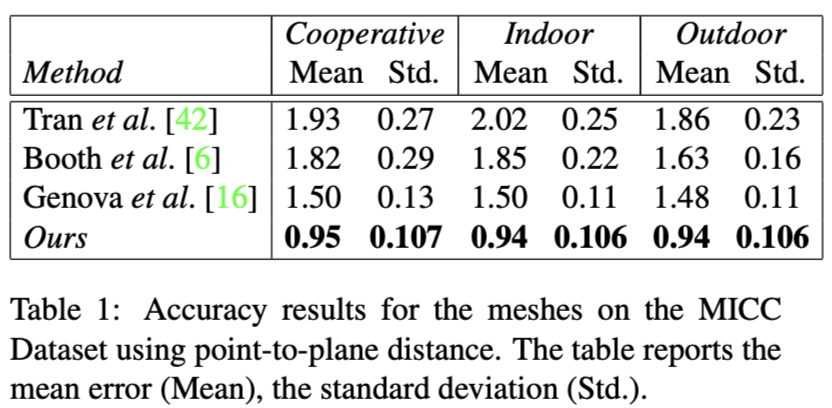
The table below shows quantitative result:
The figure below shows an ablation study. It indicates \(\ell_{pix}\) is important for lighting parameter; \(\ell_{id}\), \(\hat{\ell}_{id}\) and \(\ell_{con}\) are important for identity and expression parameter.

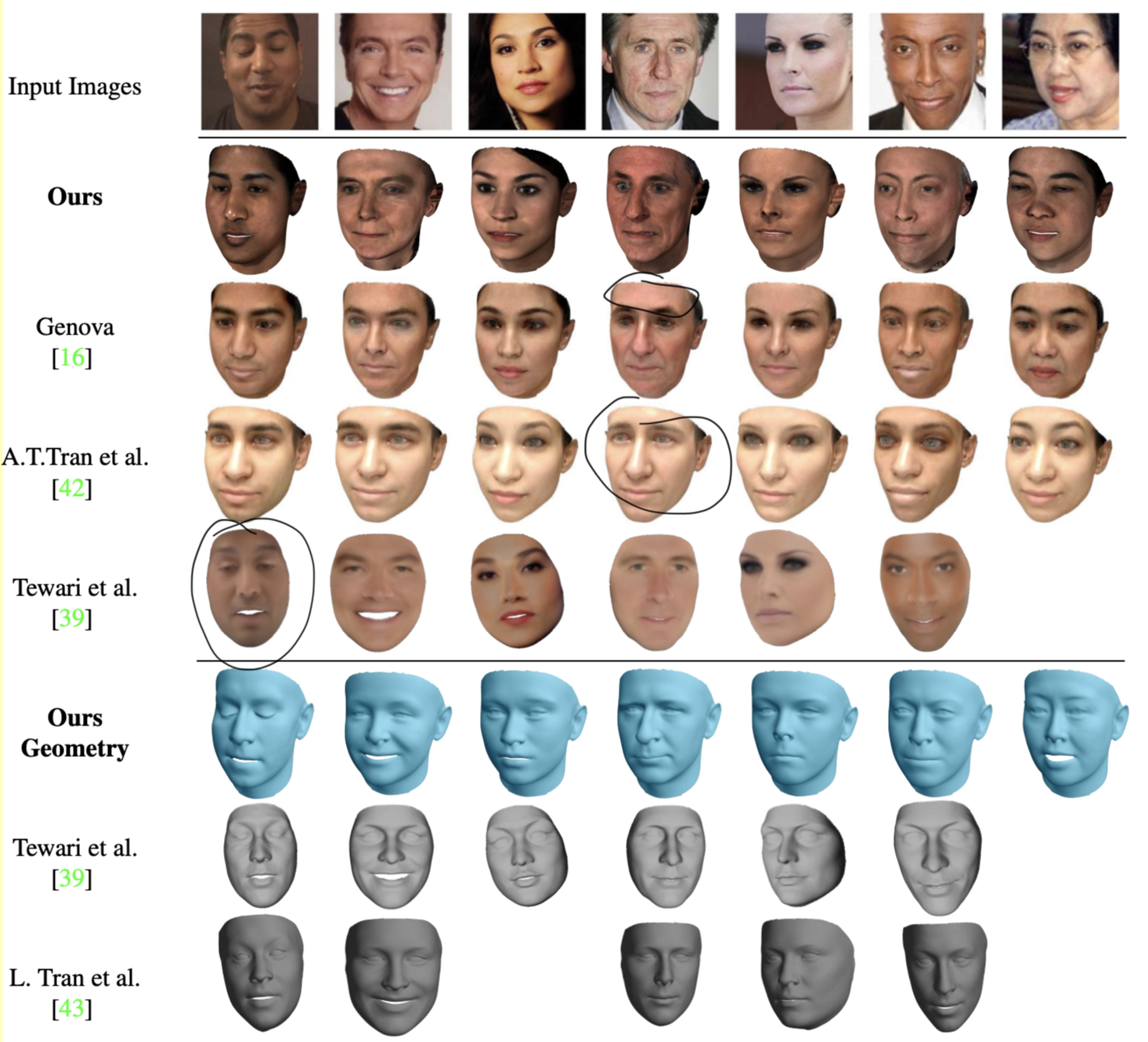
The figure below shows visual comparison of different approaches. GANFits obvious generates much more accurate results than others, especially compared with [16], details are preserved better.