Graph Convolutional Neural Network
[dcnn convolution graph cnn4g gcn spectral-convolution gat-lstm network deep-learning dcrnn gat neural Many important real-world datasets come in the form of graphs or networks: e.g., social networks. Graph Convolutional Neural Network (GCN) is a generalization of convolution neural network over the graph, where filter parameters are typically shared over all locations in the graph.
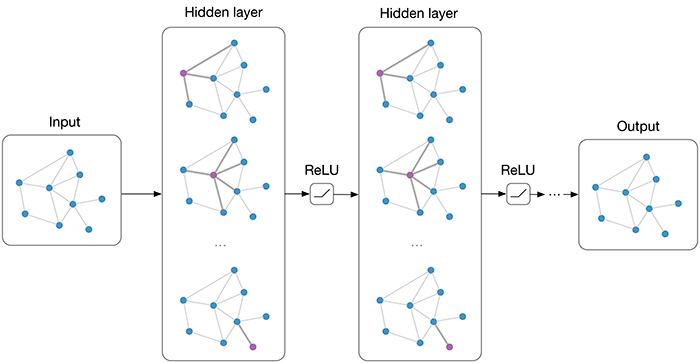
For these models, the goal is then to learn a function of signals/features on a graph G=(V,E) which takes as input:
- A feature description xi for every node i; summarized in a N×D feature matrix X (N: number of nodes, D: number of input features)
- A representative description of the graph structure in matrix form; typically in the form of an adjacency matrix A (or some function thereof) and produces a node-level output Z (an N×F feature matrix, where F is the number of output features per node).
There two types of graph convolutions:
- spectral convolution: performs the convolution in the spetral domain;
- spatial convolution: performs the convolution in the spatial domain directly.
Spectral Convolution
Spectral Convolution: Spectral Networks and Locally Connected Networks on Graphs
The convolution on the spectral can be written as the dot product in the Fourier domain:
Which can be then written as:
Some features of spectral convolution:
- the computational cost is high: O(N^3) for N nodes graph
- the perception field is N, i.e., all ndoes are involved
- the number of parameters ($\theta$) is O(N), which the CNN is constant to the size of input;
Spectral Convolution: Convolutional neural networks on graphs with fast localized spectral filtering
To address the high computational cost, eigen vector decomposition is utilized:
We can precompute the $L^k$, such that the computational cost can be reduced to O(N^2 * K).
In addition, by set the values of $L^k$ to zero for nodes whose distances are larger than some values, we could limit the perception field of the convolution as well.
Spatial Convolution
We could also do the graph convolution on the spatial domain directly. The major chanllege here is that: the convolution typically expects fixed convolution kernel, aka, fixed neighbor size for each node, which is not typically available.
DCNNs: Diffusion-convolutional neural networks
Consider t-th graph has a node l with k-th feature as $x_{t,l,k}$ and $p_{t,i,j,l}$ is the probability of transiting from $i-th$ node to $l-th$ node in $l$ hoops, the convolution can be computed as:
CNN4G: Learning convolutional neural networks for graphs
The method is intuitive:
- pick w nodes to represent the graph
- for each node, pick k neighours
- for each node, use the features of node and its neighbors as its feature map, apply convolution on it
GAT: Graph Attention Networks
This paper introduces the attention to graph convolution, which achieves state of art resutls on many tasks. The attention module computes the weight on the connections between node and its neighbors on the fly, which can be computed as:
Graph Convolution for Sequential Data
This task considers a graph whose data (e.g., node feature, edge features) changes dynamically, e.g., with regarding to time. The structure of the graph doesn’t change.
DCRNNs: Diffusion Convolutional Recurrent NeuralNetwork: Data-Driven Traffic Forecasting
The idea is intuitive: combining RNN and graph convolution network (GNN): the GNN encodes the graph information and RNN encodes the sequential information.
GAT-LSTM: Graph Attention LSTM
It combines the graph attention network with RNN.
