Knowledge Distillation A Survey
[deep-learning review distill This is my reading note on Knowledge Distillation: A Survey. As a representative type of model compression and acceleration, knowledge distillation effectively learns a small student model from a large teacher model (p. 1)
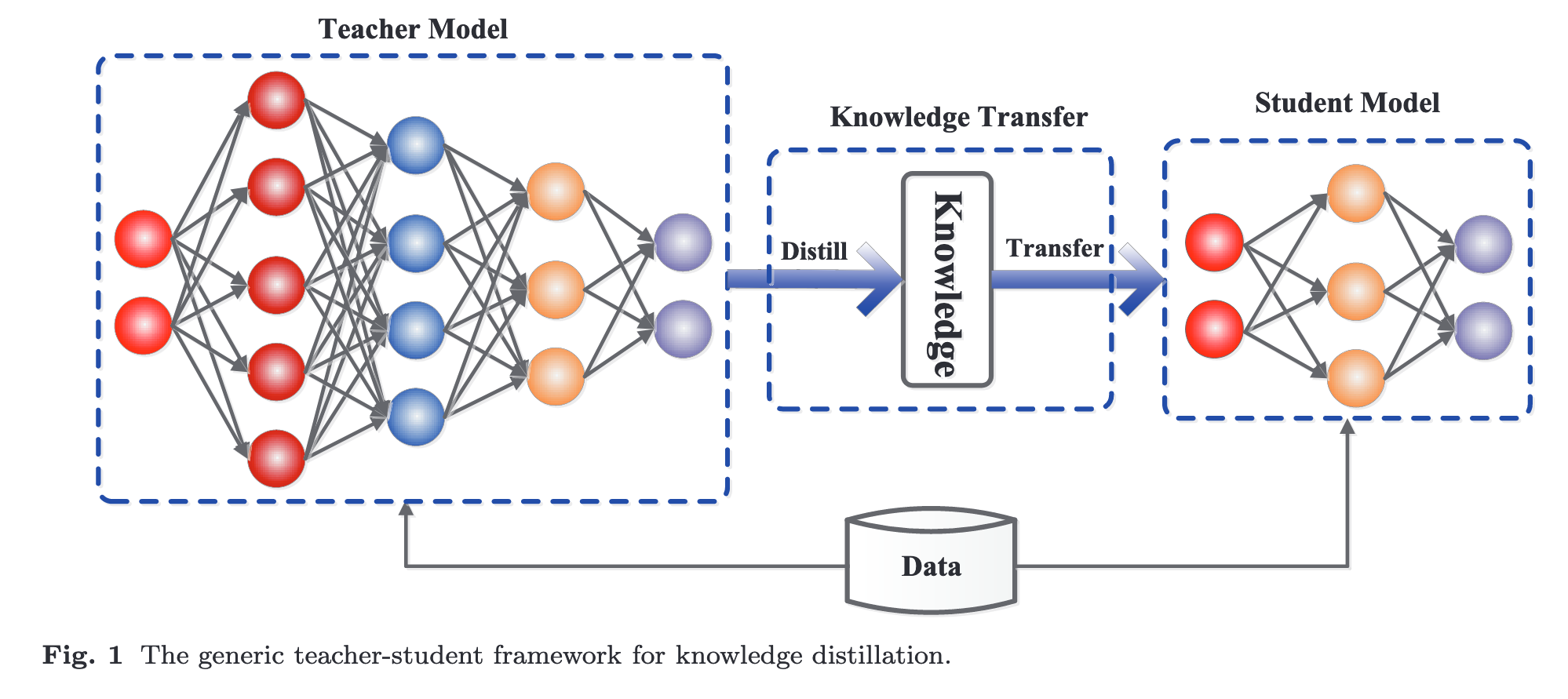
In recent years, deep neural networks have been successful in both industry and academia, especially for computer vision tasks. The great success of deep learning is mainly due to its scalability to encode large-scale data and to maneuver billions of model parameters. However, it is a challenge to deploy these cumbersome deep models on devices with limited resources, e.g., mobile phones and embedded devices, not only because of the high computational complexity but also the large storage requirements. To this end, a variety of model compression and acceleration techniques have been developed. As a representative type of model compression and acceleration, knowledge distillation effectively learns a small student model from a large teacher model. It has received rapid increasing attention from the community. This paper provides a comprehensive survey of knowledge distillation from the perspectives of knowledge categories, training schemes, teacher-student architecture, distillation algorithms, performance comparison and applications. Furthermore, challenges in knowledge distillation are briefly reviewed and comments on future research are discussed and forwarded.
Introduction
Applications of knowledge distillation:
- Parameter pruning and sharing: These methods fo- cus on removing inessential parameters from deep neural networks without any significant effect on the performance. This category is further divided into model quantization (Wu et al., 2016), model bina- rization (Courbariaux et al., 2015), structural matri- ces (Sindhwani et al., 2015) and parameter sharing (Han et al., 2015; Wang et al., 2019f).
- Low-rank factorization: These methods identify re- dundant parameters of deep neural networks by em- ploying the matrix and tensor decomposition (Yu et al., 2017; Denton et al., 2014).
- Transferred compact convolutional filters: These meth- ods remove inessential parameters by transferring or compressing the convolutional filters (Zhai et al., 2016).
- Knowledge distillation (KD): These methods distill the knowledge from a larger deep neural network into a small network (Hinton et al., 2015). (p. 2)
Specifically, Urner et al. (2011) proved that the knowledge transfer from a teacher model to a student model using unlabeled data is PAC learnable (p. 2)
Successful distillation relies on data geometry, optimization bias of distillation objective and strong monotonicity of the student classifier (p. 3). Empirical results show that a larger model may not be a better teacher because of model capacity gap (Mirzadeh et al., 2020). Experiments also show that distillation adversely affects the student learning. (p. 3)
Knowledge
Response-Based Knowledge
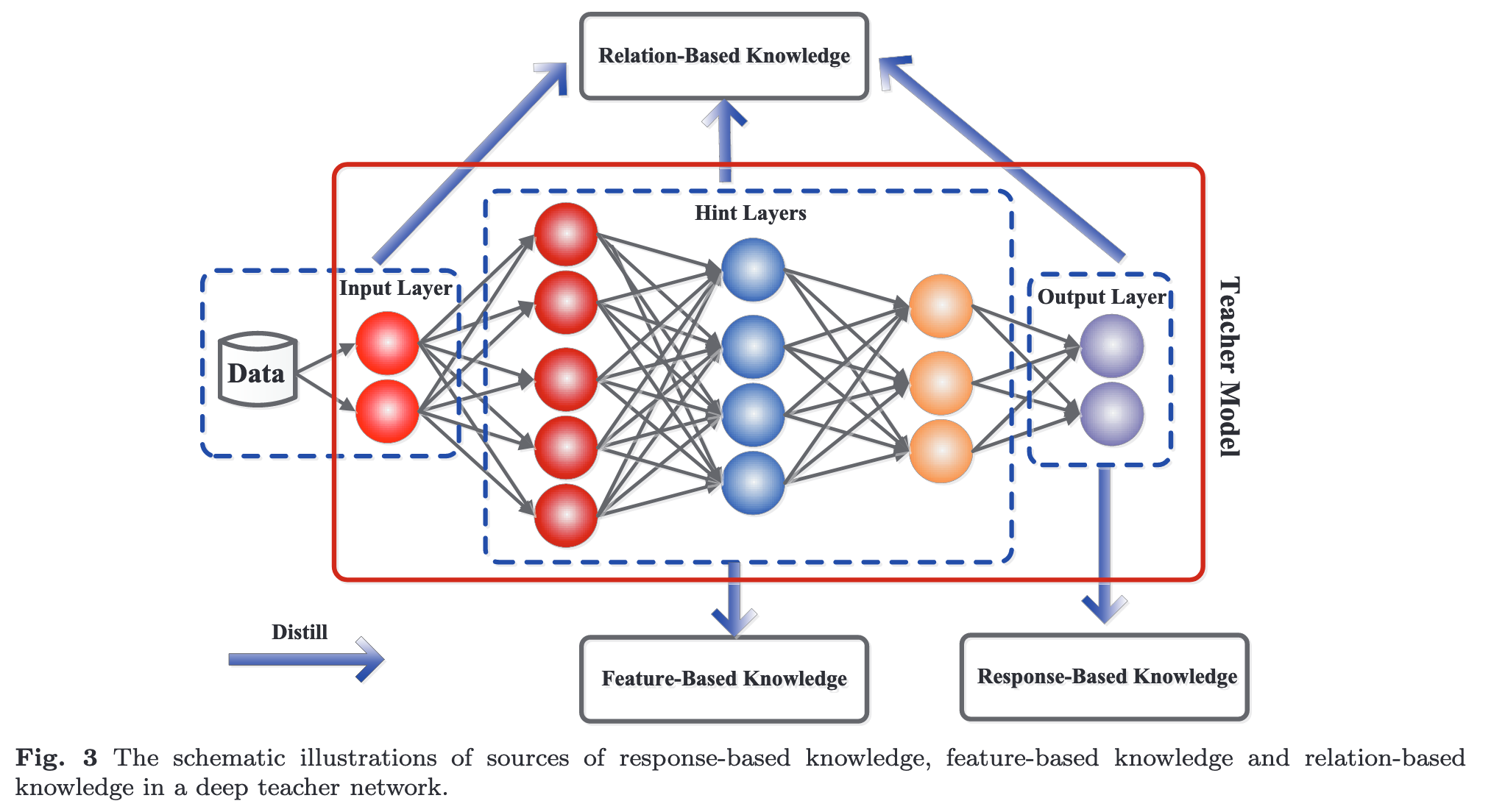
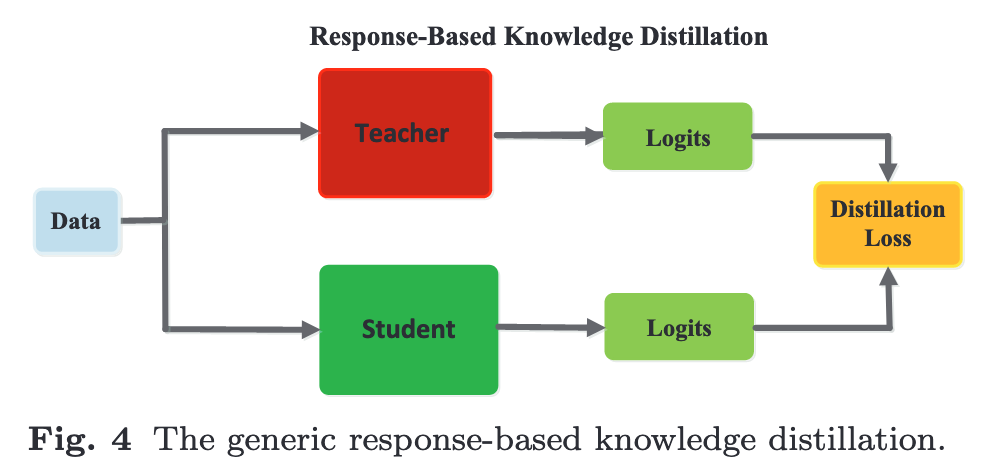
Response-based knowledge usually refers to the neural response of the last output layer of the teacher model. The main idea is to directly mimic the final prediction of the teacher model. The response-based knowledge distillation is simple yet effective for model compres- sion, and has been widely used in different tasks and applications. (p. 5)
Generally, \(LR(p(z_t, T ), p(z_s, T ))\) often employs Kullback- Leibler divergence loss (p. 5)
Feature-Based Knowledge
From another perspective, the effectiveness of the soft targets is analogous to label smoothing (Kim and Kim, 2017) or regulariz- ers (Muller et al., 2019; Ding et al., 2019). However, the response-based knowledge usually relies on the output of the last layer, e.g., soft targets, and thus fails to address the intermediate-level supervision from the teacher model, which turns out to be very important for representation learning using very deep neural networks (p. 5)
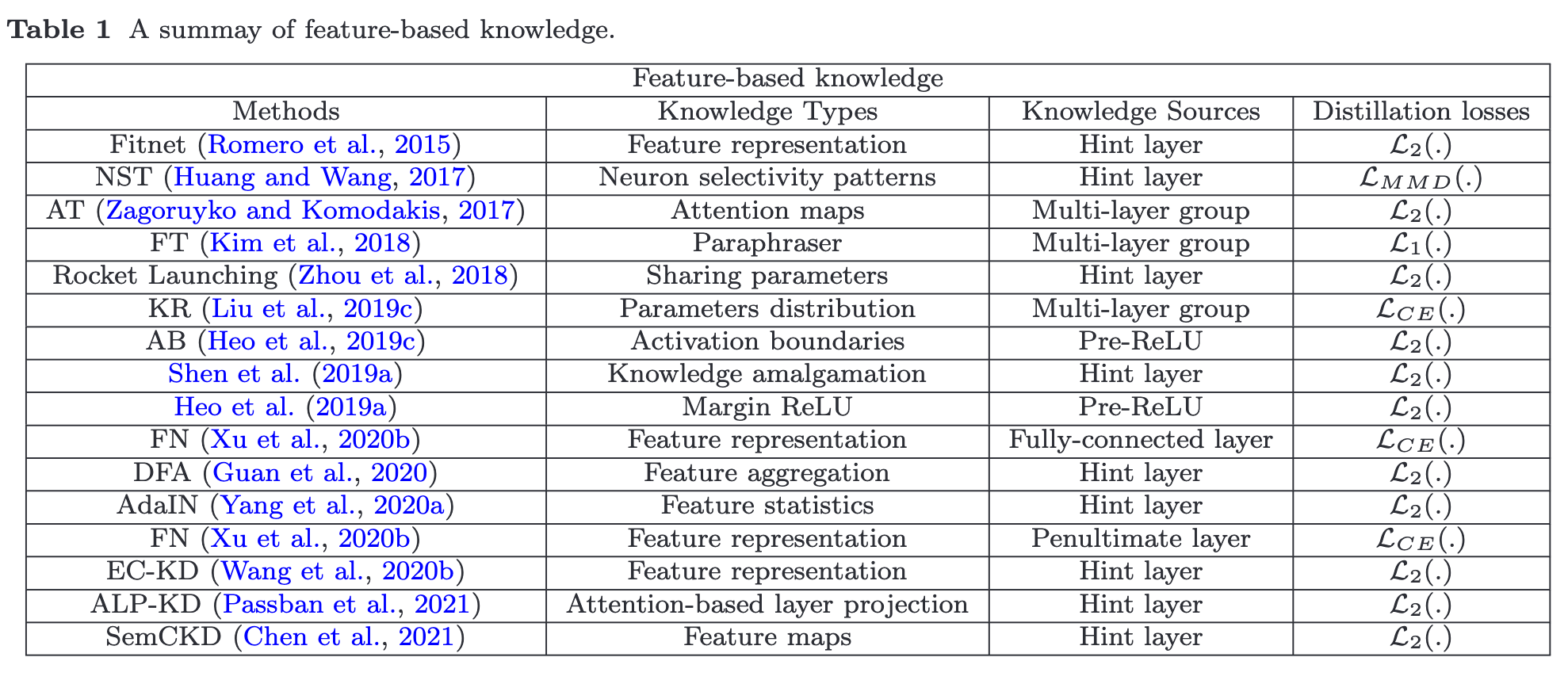
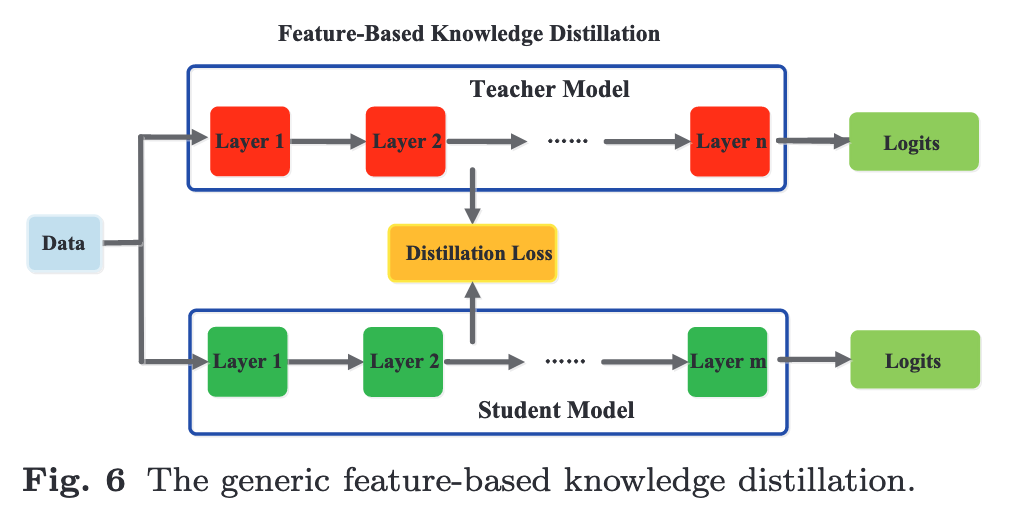
Though feature-based knowledge transfer provides favorable information for the learning of the student model, how to effectively choose the hint layers from the teacher model and the guided layers from the student model remains to be further investigated (p. 7)
Relation-Based Knowledge
To explore the relationships between different feature maps, Yim et al. (2017) proposed a flow of solution process (FSP), which is defined by the Gram matrix between two layers. The FSP matrix summarizes the relations between pairs of feature maps. It is calculated using the inner products between features from two lay- ers. Using the correlations between feature maps as the distilled knowledge, knowledge distillation via singular value decomposition was proposed to extract key infor- mation in the feature maps (p. 7)
The graph knowledge is the intra-data relations between any two feature maps via multi-head attention network. To explore the pairwise hint information, the student model also mimics the mutual information flow from pairs of hint layers of the teacher model (p. 7)
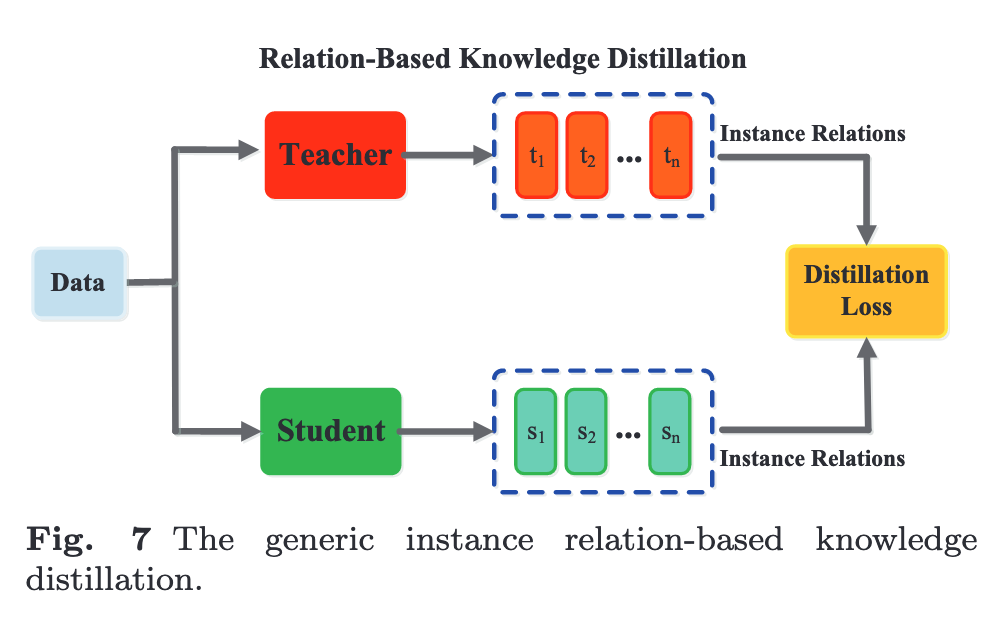
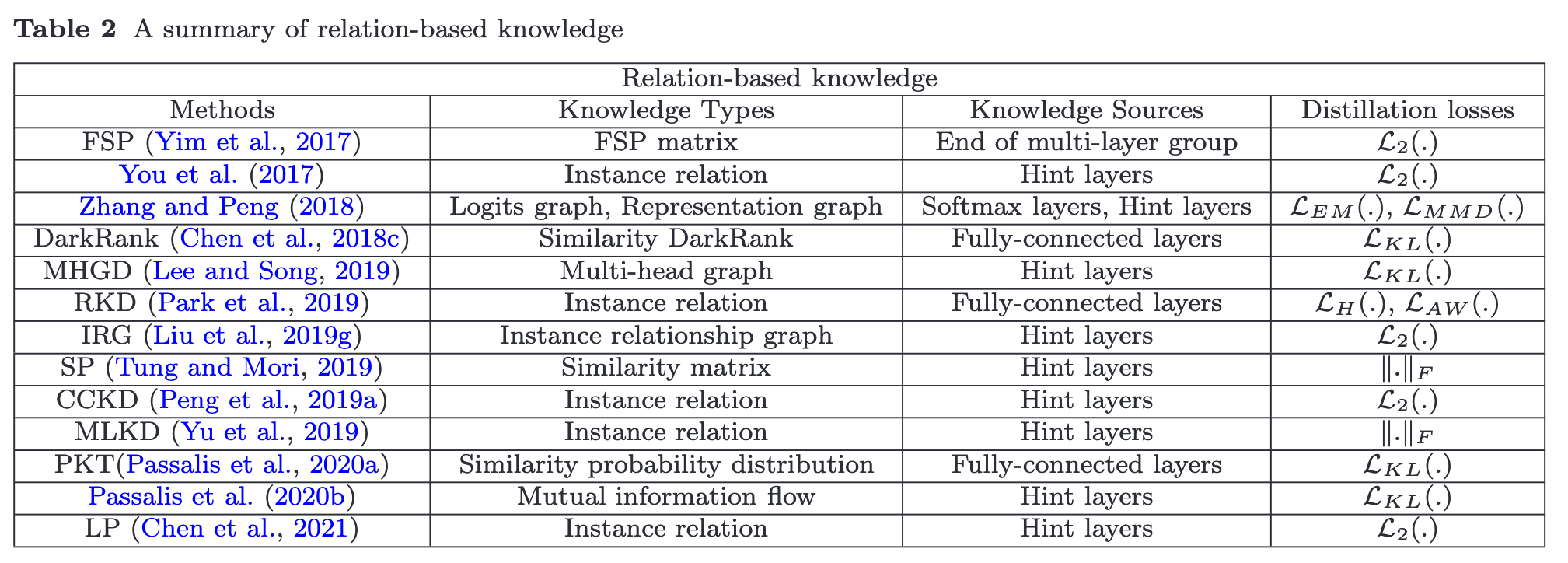
$L_{EM} (.)$, $L_H(.)$, $L_{AW} (.)$ and $\lVert\cdot\rVert_F$ are Earth Mover distance, Huber loss, Angle-wise loss and Frobenius norm, respectively. A (p. 8)
Distillation Schemes
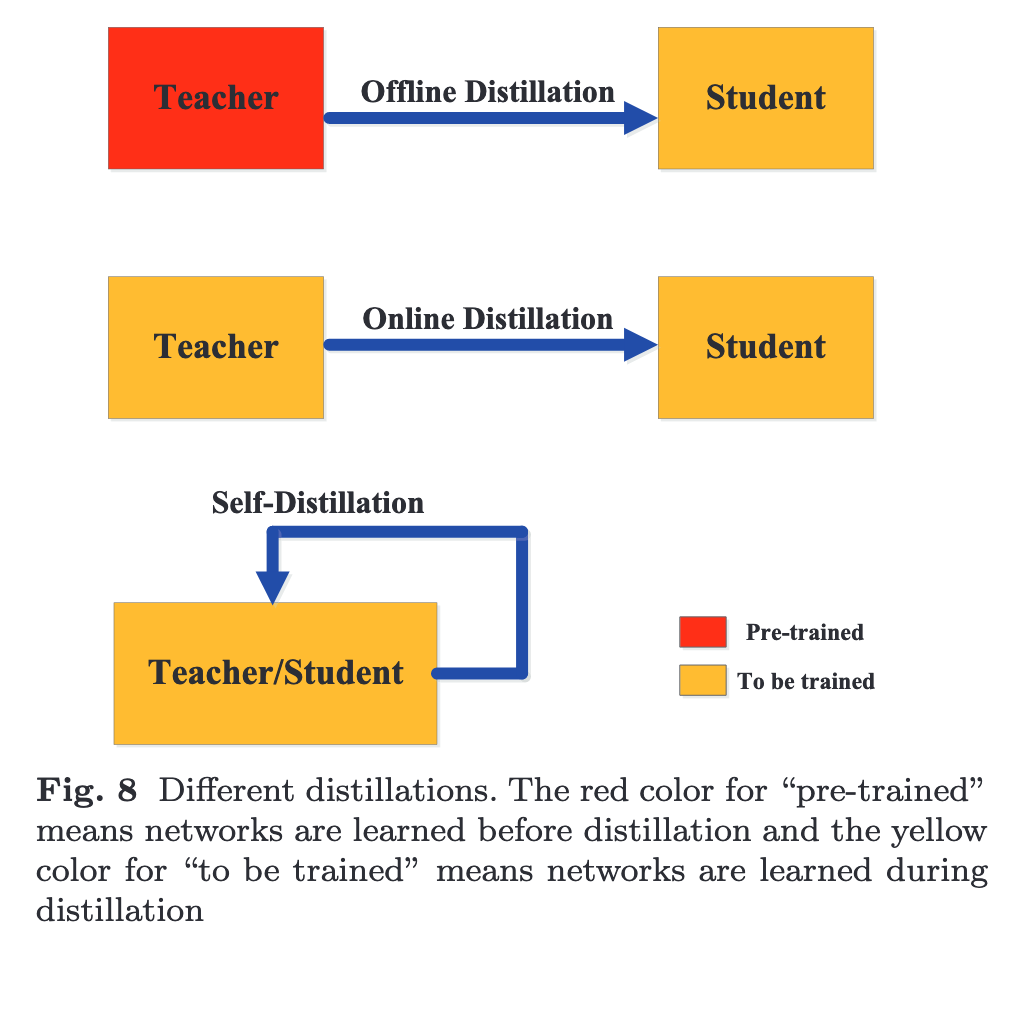
Offline Distillation
The offline distillation methods usually employ one- way knowledge transfer and two-phase training pro- cedure. However, the complex high-capacity teacher model with huge training time can not be avoided, while the training of the student model in offline distillation is usually efficient under the guidance of the teacher model. Moreover, the capacity gap between large teacher and small student always exists, and student often largely relies on teacher. (p. 9)
Online Distillation
online distillation is proposed to further improve the performance of the student model, especially when a large-capacity high perfor- mance teacher model is not available (p. 9)
Specifically, in deep mutual learning (Zhang et al., 2018b), multiple neural networks work in a collab- orative way. Any one network can be the student model and other models can be the teacher during the training process (p. 9)
- further introduced auxiliary peers and a group leader into deep mutual learning to form a diverse set of peer models (p. 9)
- proposed a multi-branch architecture, in which each branch indicates a student model and different branches share the same backbone network (p. 9)
Co-distillation in parallel trains multiple models with the same architectures and any one model is trained by transferring the knowledge from the other models. Recently, an online adversarial knowledge distillation method is proposed to simultaneously train multiple networks by the discriminators using knowl- edge from both the class probabilities and a feature map (p. 9)
Online distillation is a one-phase end-to-end train- ing scheme with efficient parallel computing. However, existing online methods (e.g., mutual learning) usually fails to address the high-capacity teacher in online settings, making it an interesting topic to further ex- plore the relationships between the teacher and student model in online settings. (p. 9)
Self-Distillation
Specifically, Zhang et al. (2019b) proposed a new self-distillation method, in which knowledge from the deeper sections of the network is distilled into its shallow sections (p. 9) The network utilizes the attention maps of its own layers as distillation targets for its lower layers (p. 9) knowledge in the earlier epochs of the network (teacher) is transferred into its later epochs (student) to sup- port a supervised training process within the same network. (p. 9)
To be specific, Yuan et al. proposed teacher-free knowledge distillation meth- ods based on the analysis of label smoothing regularization (p. 10)
Distillation Algorithms
Adversarial Distillation
many adversarial knowledge distillation methods have been proposed to enable the teacher and stu- dent networks to have a better understanding of the true data distribution (p. 11)
In the first category, an adversarial genera- tor is trained to generate synthetic data, which is either directly used as the training dataset (p. 11). It utilized an adversarial generator to generate hard examples for knowledge transfer (p. 11)
\[L_{KD} = L_G(F_t(G(z)), F_s(G(z)))\]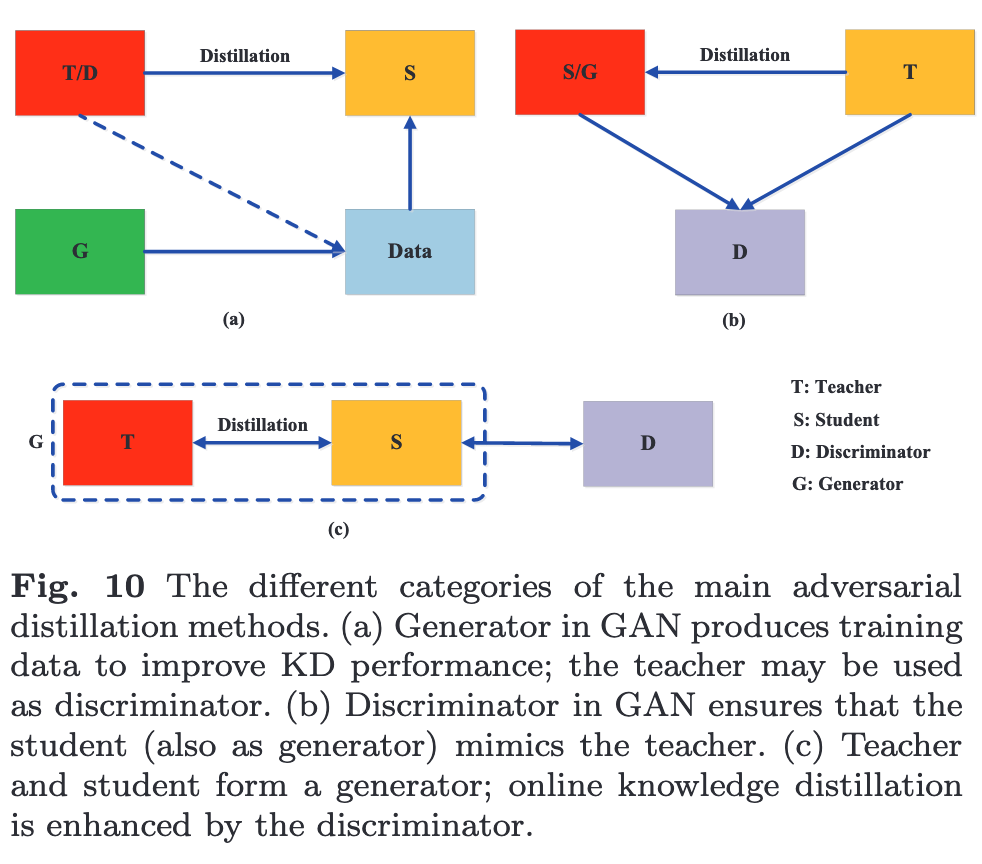
To make student well match teacher, a discriminator in the second category is introduced to distinguish the samples from the student and the teacher models (p. 12)
\(L_{GANKD} =L_{CE}(G(F_s(x)), y) + \alpha L_{KL}(G(F_s(x)), F_t(x)) + \beta L_{GAN}( F_s(x), F_t(x))\)
Multi-Teacher Distillation
which one teacher trans- fers response-based knowledge to the student and the other teacher transfers feature-based knowledge to the student (p. 13). Another workrandomly selected one teacher from the pool of teacher networks at each iteration. (p. 13)
Graph-Based Distillation
The core of attention transfer is to define the attention maps for feature embedding in the layers of a neural network. That is to say, knowledge about feature embedding is transferred using attention map functions. (p. 15)
