NeuMan Neural Human Radiance Field from a Single Video
[cnn animatable-nerf colmap human-nerf neural-body mask-rcnn smpl mlp deep-learning body-pose differential-rendering st-nerf body nerf human neural-actor vid2actor neuman NeuMan: Neural Human Radiance Field from a Single Video proposes a novel framework to reconstruct the human and the scene that can be ren- dered with novel human poses and views from just a single in-the-wild video. Given a video captured by a moving camera, we train two NeRF models: a human NeRF model (condition on SMPL) and a scene NeRF model. Our method is able to learn subject specific details, including cloth wrinkles and ac- cessories, from just a 10 seconds video clip, and to provide high quality renderings of the human under novel poses, from novel views, together with the background.
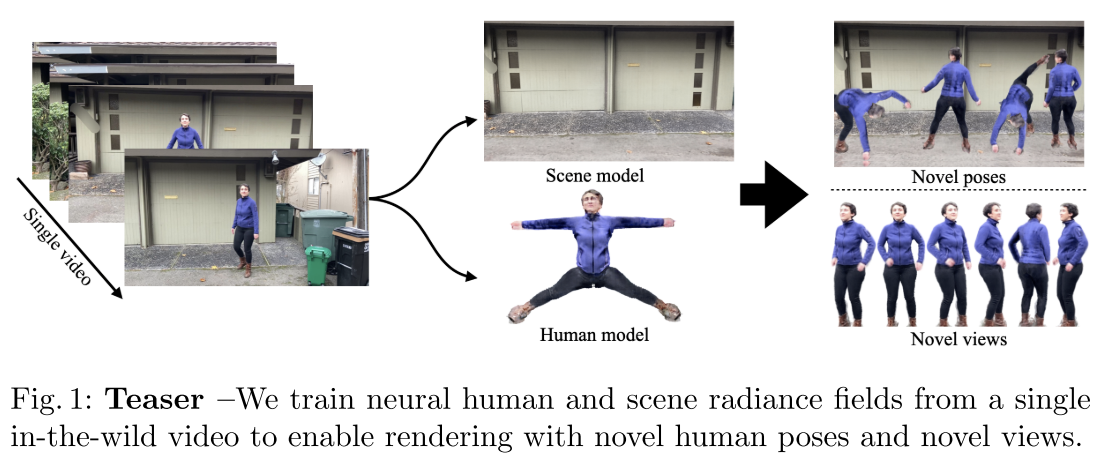
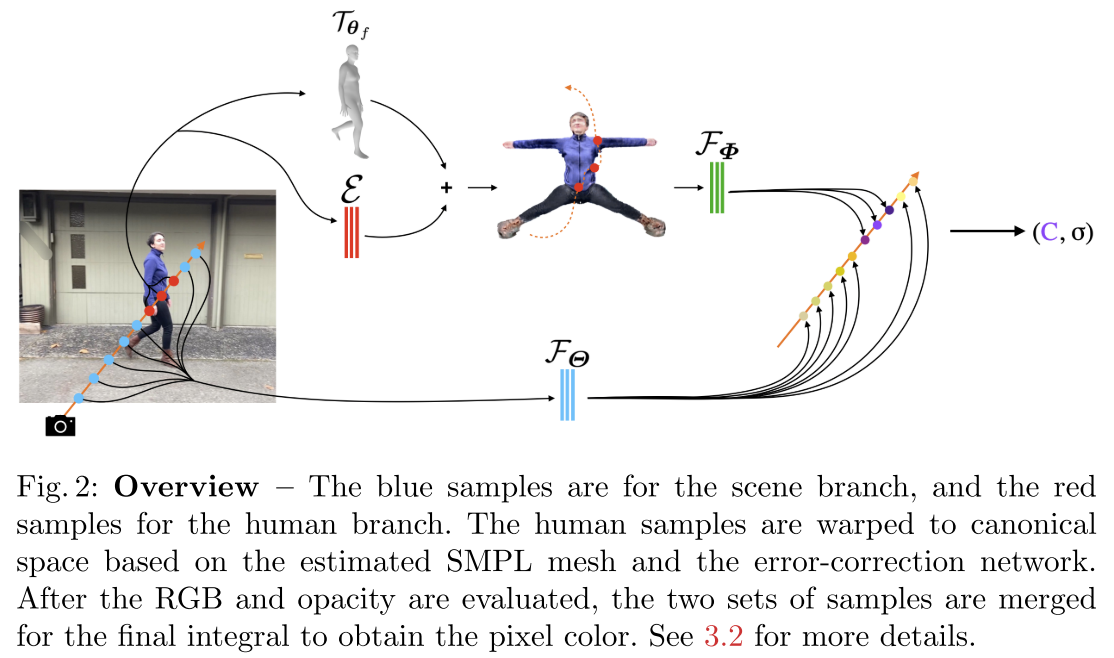
Figure below shows an overview of NeuMan. Given the input video, COLMAP is first applied to estimate the camera pose. For each frame, it applies Mask-RCNN to segment the human from the scene. Then the background is used to train the scene NeRF \(\mathcal{F}_\Theta\). For the segmented human, SMPL is applied to estimate the body pose (T), together with the error correction network \(\epsilon\), it canonize the body pose to 大. A human NeRF \(\mathcal{F}_\Phi\) is then learned in this canonized pose.
Related Work
Various efforts have been made towards NeRF models conditioned by explicit human models, such as SMPL or 3D skeleton:
- Methods require multi-camera setup
- Neural Body [32] associates a latent code to each SMPL vertex, and use sparse convolution to diffuse the latent code into the volume in observation space.
- Neural Actor [19] learns the human in the canonical space by a volume warping based on the SMPL [23] mesh transformation, it also utilize a texture map to improve the final rendering quality.
- Animatable NeRF [31] learns a blending weight field in both observation space and canonical space, and optimize for a new blending weight field for novel poses.
- ST-NeRF [12] separates the human into each 3D bounding box, and learns the dynamic human within each bounding box. It doesn’t require to estimate the precise human geometry, but it cannot extrapolate to unseen poses since it is dependent on time(frame).
- Methods works with a single video
- HumanNeRF [47] represents motion as a combi- nation of the skeletal and the non-rigid transformations, causing ambiguous or unknown transformations under novel poses, while ours mitigates the ambiguity by using explicit human mesh.
- Another similar work is Vid2Actor [46], which builds animatable human from a single video by learning a voxelized canonical volume and skinning weights jointly. Although with similar goals, our method is able to reconstruct sharp human geometry with less than 40 images, comparing to thousands frames are required for Vid2Actor, our method is data-efficient.
Scene NeRF Model
The scene NeRF model is analogous to the background model in traditional motion detection work [41,6,16], except it’s a NeRF. For the scene NeRF model, we construct a NeRF model and train it with only the pixels that are deemed to be from the background. Given M(r)=0 means the background and C for color:
\[L_{s,rgb}(r)=(1-M(r))\lVert C_s(r)-\hat{C}(r)\rVert\]As in Video-NeRF [49], simply minimizing Eq. 3 leads to ‘hazy’ objects floating in the scene. Therefore, following Video-NeRF [49], we resolve this by adding a regularizer on the estimated density, and forcing it to be zero for space that should be empty—the space between the camera and the scene.
\[L_{s,empty}=\int_{t_n}^{\alpha \hat{z}_r}{\sigma_s(r(t))d_t}\]For retrieving human segmentation maps we apply Mask-RCNN [10]. We further dilate the human masks by 4% to ensure the human is completely masked out. With the estimated camera poses and the background masks, we train the scene NeRF model only over the background.
Human NeRF Model
Human Pose Estimation
To build a human model that can be pose-driven, we require the model to be pose independent. Therefore, we define a canonical space based on the 大-pose (Da-pose) SMPL [23] mesh. To render a pixel of a human in the observation space with this model, we transform the points along that ray into the canonical space.
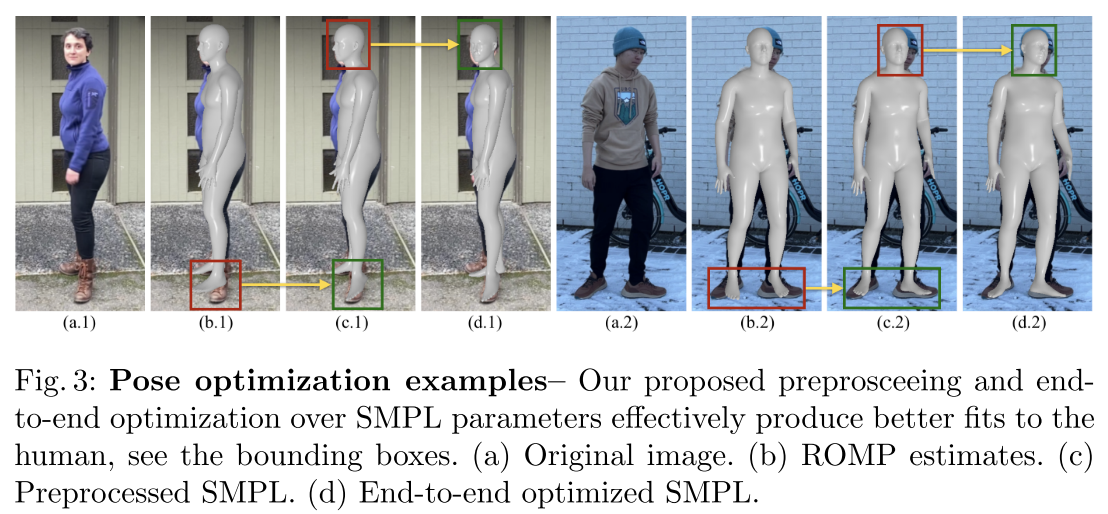
In each frame f, given a 3D point \(x_f = r_f(t)\) in observation space and the corresponding estimated SMPL mesh \(\theta_f\) obtained from preprocessing 3.2, we transform it into the canonical space by following the rigid transformation of its closest point on the mesh. We denote this mesh-based transform as T such that \(\tilde{x}_f = T_{\theta_f} (x_f)\). This transformation, however, relies completely on the accuracy of \(\theta_f\), which is not reliable even with the recent state of the art. To mitigate the misalignment between the SMPL estimates and the underlying human, we propose to jointly optimize \(\theta_f\) together with the neural radiance field while training. Furthermore, to account for the details that can not be expressed by the SMPL model, we introduce the error-correction network \(\epsilon\), an MLP that corrects for the errors in the warping field.
\[\tilde{x}_f=T_{\theta_f}(x_f)+\epsilon(x_f,f)\]The error-correction net is only used during training, and is discarded for rendering with validation and novel poses. Please refer to Fig 3 for an ablation study on pose estimation.
Human NeRF
Similar as scene NeRF model, only human region is considered for human NeRF, i.e., M(r)=1:
\[L_{h,rgb}=M(r)\lVert C_h(r)-\hat{c}(r)\rVert\]We use Lmask to enforce the accumulated alpha map from the human NeRF to be similar to the detected human mask. Here \(\alpha(r)\) is the transparency of a pixel.
\[L_{mask}=M(r)\lVert 1-\alpha_h(r)\rVert\]To avoid blobs in the canonical space and semi-transparent canonical human, we enforce the volume inside the canonical SMPL mesh to be solid, while enforcing the volume outside the canonical SMPL mesh to be empty, given by
\[L_{smpl}(\hat{x}_f,\sigma_h)=\left\{\begin{matrix} \lVert 1-\sigma_h\rVert & \mbox{if }\hat{x}_f\mbox{ inside SMPL mesh} \\ \lvert \sigma_h\rvert & \mbox{otherwise} \\ \end{matrix}\right.\]Moreover, we utilize hard surface loss Lhard [35] to mitigate the halo around the canonical human. To be specific, we encourage the weight of each sample to be either 1 or 0 given by (w is the transparency where the ray terminates)
\[L_{hard}=-\log{(e^{-|w|}+e^{-|1-w|})}\]By rendering a random straight ray in the canonical volume, we encourage the accumulated alpha values to be either 1 or 0.
\[L_{edge}=-\log{(e^{-|\alpha|}+e^{-|1-\alpha_c|})}\]Scene Human Alignment
To compose a scene with a human in novel view and pose, and to train the two NeRF models, we align the coordinate systems in which the two NeRF models lie. This is, in fact, a non-trivial problem, as human body pose estimators [13,42,18] operate in their own camera systems with often near-orthographic camera models.
To deal with this issue, we first solve the Perspective-n-Point (PnP) problem [14] between the estimated 3D joints and the projected 2D joints with the camera intrinsics from COLMAP. This solves the alignment up to an arbitrary scale. We then assume that the human is standing on a ground at least in one frame, and solve for the scale ambiguity by finding the scale that allows the feet meshes of the SMPL model to touch the ground plan. We obtain the ground plane by applying RANSAC.

Rendering
To render a pixel, we shoot two rays, one for the human NeRF, and the other for the scene NeRF. We evaluate the colors and densities for the two sets of samples along the rays. We then sort the colors and the densities in the ascending order based on their depth values, similar to ST-NeRF [12]. Finally, we integrate over these values to obtain the pixel using:
\[C(r)=\sum_{i=1}^N{w_i c_i}\mbox{ where }w_i=e^{-\sum_{j=1}^{i-1}{\sigma_j\delta_j}}(1-e^{-\sigma_i\delta_i})\]The transparency of a pixel or alpha, could be computed as \(\alpha(r)=\sum_{i=1}^N{w_i}\)
The telegathering example in Fig 7 doesn’t look high quality at all to me. It is more like mediocre photoshope copy and paste.
