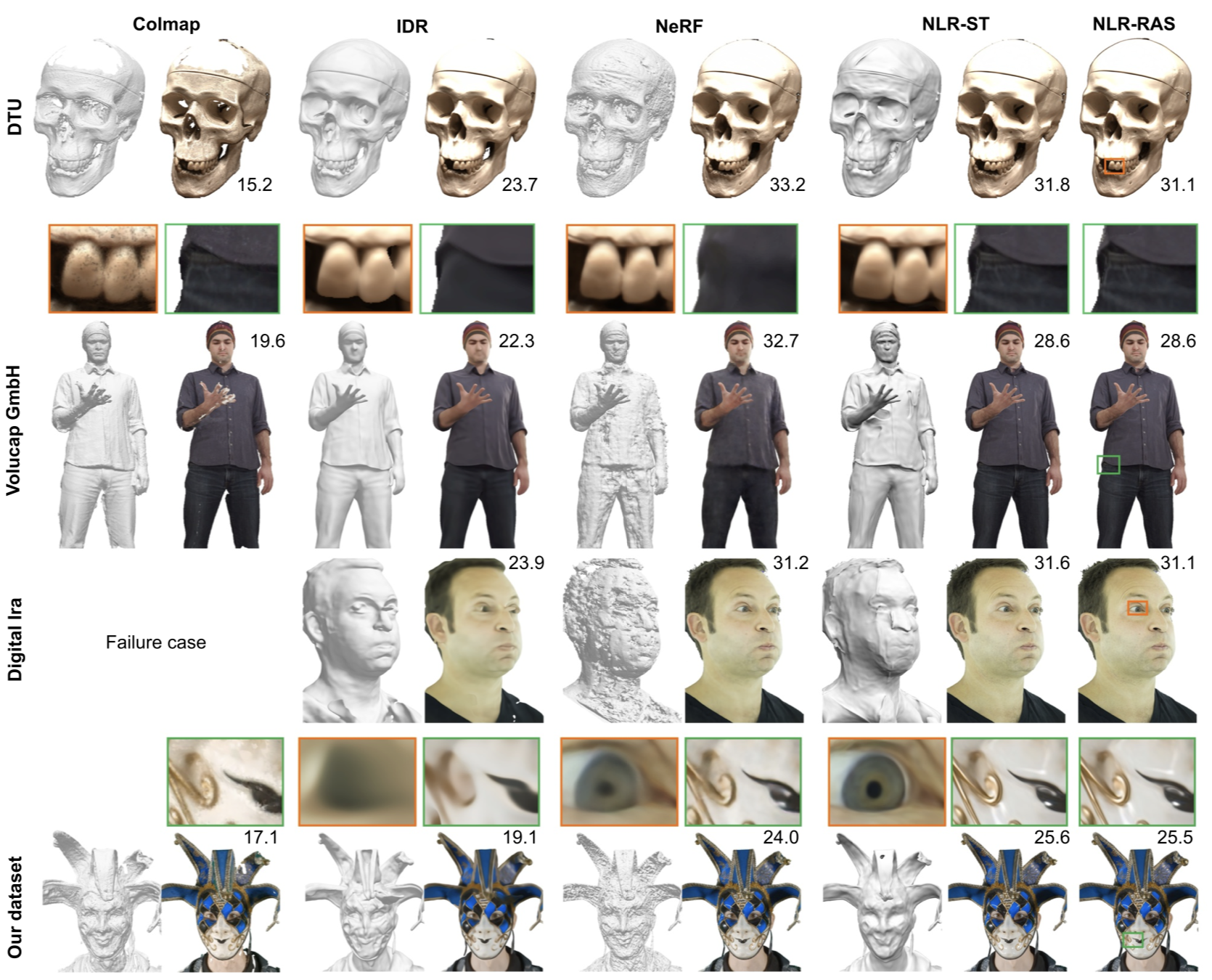
Neural Lumigraph Rendering
[cvpr differetial-render nerf deep-learning synthetic 2021 3d-mesh riren lumigraph best-paper Neural Lumigraph Rendering was accepted for CVPR 2021 Oral and best paper candidate. This paper proposes a method which performs on par with NeRF on view interpolation tasks while providing a high-quality 3D surface that can be directly exported for real-time rendering at test time. code is publically available.
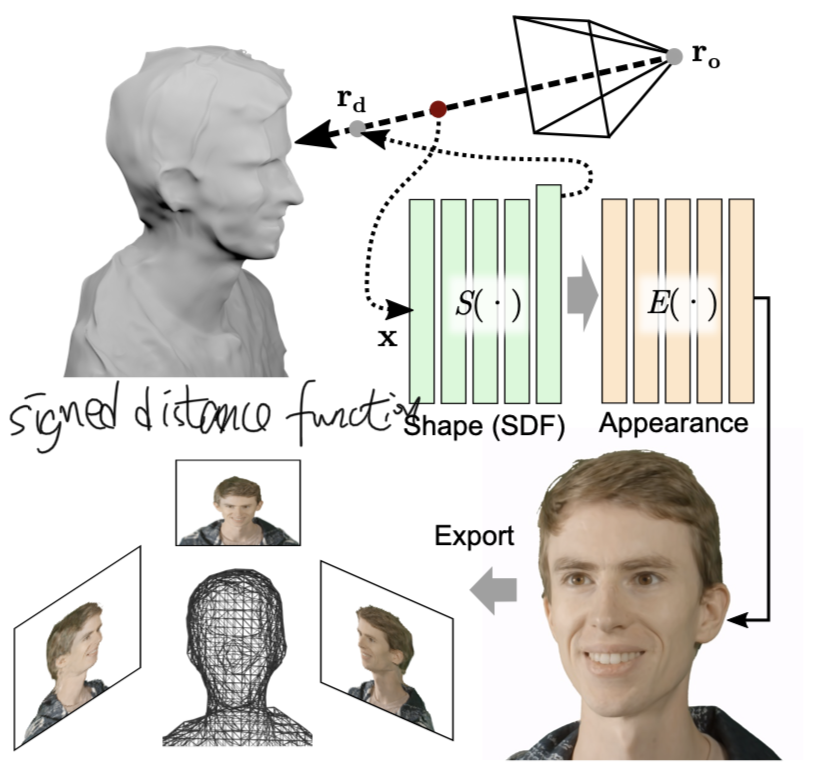
The major contribution of this paper is that it addresses the speed limitation of neural radiance field method, which is state of art neural rendering method, by adopting an SDF-based sinusoidal representation network (SIREN) as the backbone of our neural rendering system and export a 3D face mesh could be used for real time rendering.
Representation
We express the continuous shapes of a scene as the zero level set \(S_0=\{x\vert S(x)=0\}\) of a signed distance function (SDF) \(S(x;\theta):\mathbb{R}^3\to\mathbb{R}\) where \(x\in\mathbb{R}^3\) is a location in 3D space and \(\theta\) are the learnable parameters of our SIREN-based SDF representation.
RIREN is a MLP network is uses sin function as the activation function instead of ReLU or others.
we model appearance as a spatially varying emission function, or radiance field, E for directions \(r_d\in\mathbb{R}^3\) defined in a global coordinate system. This formulation does not allow for relighting but it enables photorealistic reconstruction of the appearance of a scene under fixed lighting conditions.
Together, the radience field is written as:
\[E(x,r_d,n,\theta,\phi):\mathbb{R}^9\to\mathbb{R}^3\]here n is surface normal, \(\theta\) is the parameter for shape network and \(\phi\) is the parameter for radiance network.
Neural Rendering
We solve this task in two steps:
- We find the 3D surface as the zero-level set \(S_0\) closest to the camera origin along each ray;
- We resolve the appearance by sampling the local radiance E.
To export mesh for rendering, the following two steps are need respectively:
- we use the marching cubes algorithm to extract a high-resolution surface mesh from the SDF S voxelized at a resolution of 512;
- To export the appearance, we resample the optimized emissivity function E to synthesize projective textures Ti for N camera poses and corresponding projection matrices.
Training
We supervise our 3D representation using a set of m multi-view 2D images \(I=\mathbb{R}^{m\times w\times h\times 3}\) with known object masks \(M=\mathbb{R}^{m\times w\times h}\) where 1 marks foreground. The following regularization term is used:
- First, we minimize an L1 image reconstruction error for the true foreground pixels;
- Second, we regularize the S by an eikonal constraint to enforce its metric properties important for efficient sphere tracing
- Third, we restrict the coarse shape by enforcing its projected pattern to fall within the boundaries of the object masks
- linearize the angular behavior using a smoothness term.
We optimize the loss in mini-batches of 50,000 individual rays sampled uniformly across the entire training dataset. We have found a large batch size and uniform ray distribution to be critical to prevent local overfitting of SIREN, especially for the high-frequency function E. We implement the MLPs representing S and E as SIRENs with 5 layers using 256 hidden units each.
Experiment Result
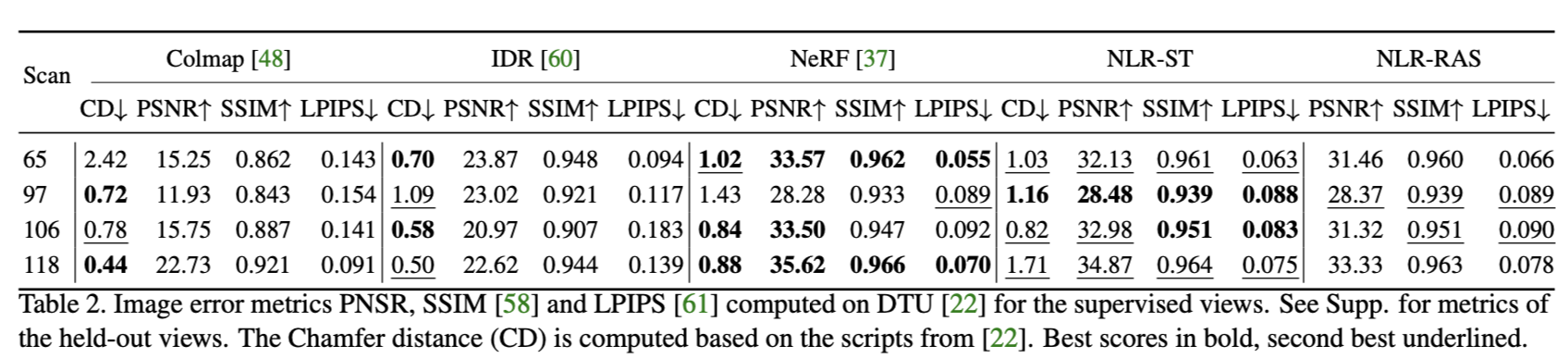
Quantiative evaluation is available as below (ST: sphere-trace, RAS: rasterize):
Some visual comparisons are available below, which shows that the propose method NLR preserves more details and is more sharp.