NeX Real-time View Synthesis with Neural Basis Expansion
[cvpr differetial-render nerf deep-learning synthetic 2021 best-paper multiplane-image NeX: Real-time View Synthesis with Neural Basis Expansion is paper from a group from Thailand and was accepted for CVPR 2021 Oral and best paper candidate. This paper proposes a method of synthesizing views from multiplane images, which is real time with view-dependent effects such as the reflection. The code is published is as well.
The major contribution of this paper is representing each color as a function of the viewing angle and approximate this function using a linear combination of spherical basis functions learned from a neural network. It is capable of capturing high frequency details explictly.
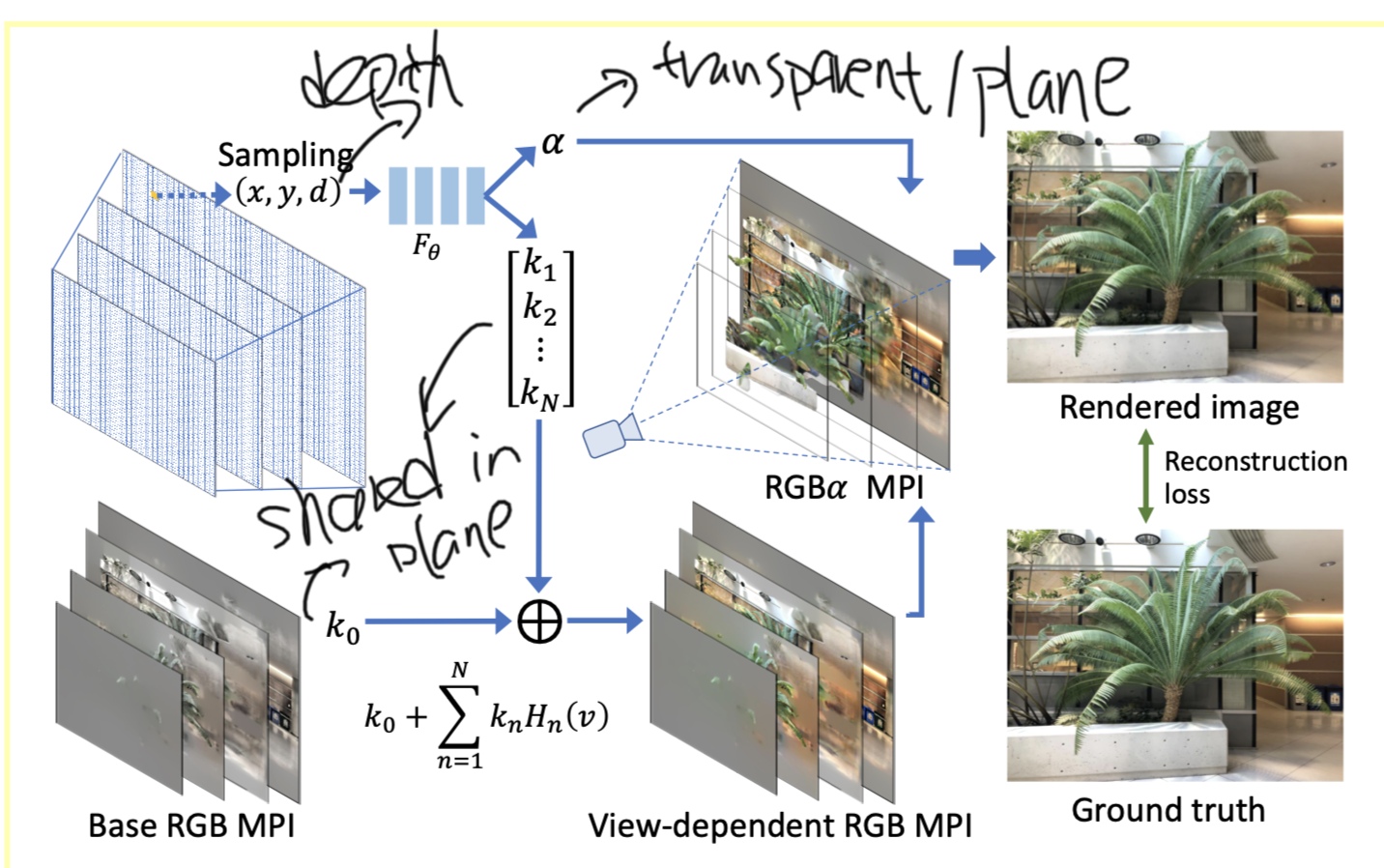
Multiplane Image
Multiplane image is a 3D scene representation that consists of a collection of D planar images, each with dimension \(H\times W\times 4\) where the last dimension contains RGB values and alpha transparency values. These planes are scaled and placed equidistantly either in the depth space (for bounded close-up objects) or inverse depth space (for scenes that extend out to infinity) along a reference viewing frustum (see figure above).
However, the dataset provided the author seems to be images captured at slightly different view angle, instead of MPI defintion.
One main limitation of MPI is that it can only model diffuse or Lambertian surfaces, whose colors appear constant regardless of the viewing angle. To solve this, this paper propsoes to parameterize each color value as a function of the viewing direction \(v = (v_x, v_y, v_z)\). This defines a mapping function from view direction to color as \(\mathcal{C}(v):\mathbb{R}^3\to\mathbb{R}^3\).
However, to define a function for viewing direction for each pixel is prohibitive, as a result, the paper proposes to approximate this function as linear combination of learnable basis function \(h_n(v):\mathbb{R}^3\to\mathbb{R}\). Thus, for pixel p at direction v, the color could be written as:
\[\mathcal{C}^p(v)=k_0^p+\sum_n{h_n(v)k_n^p}\]Here we could view k as the texture and h as the lighting, which is shared cross pixels.
Proposed Method
Given a set of multiview images (around 12 or more) of a scene, our goal is to construct a 3D representation that can render novel views with view-dependent effects in real time. This is achieved by using two separate MLPs:
- one for predicting per-pixel parameters (k) given the pixel location: \(F_\theta:x\to(\alpha,k_0,k_1,...,k_n)\), here x contains 2d location and depth.
- and the other for predicting all global basis functions (h) given the viewing angle: \(G_\phi:v\to(H_1,H_2,...,H_n)\)
To avoid overfitting, \(k_0,k_1,...,k_n\) are shard cross all planes. For location, position encoding is used which project x, y each into 20 dimensions and depth into 16 dimensions as \(p(u)=[\sin(2^0\frac{\pi}{2}u),\cos(2^0\frac{\pi}{2}u),...,\sin(2^k\frac{\pi}{2}u),\cos(2^k\frac{\pi}{2}u)]\).
The model is trained by comparing the rendered images to the input images, more specifically the loss function is:
\[\ell_{rec}(\hat{I},I)=\lVert I-\hat{I}\rVert_2+w\lVert \Delta I-\Delta\hat{I}\rVert_1\]This network uses 6 fully-connected LeakyReLU layers, each with 384 hidden nodes. The output \(\alpha\) uses a sigmoid activation, and the others use tanh activations. For Gφthat predicts the basis functions, we use positional encoding of the input viewing direction with 12 dimensions including 6 dimensions for \(v_x\) and \(v_y\). This network uses 3 fully-connected LeakyReLU layers with 64 hidden nodes to output 8 dimensions of \(H_\phi(v)\)
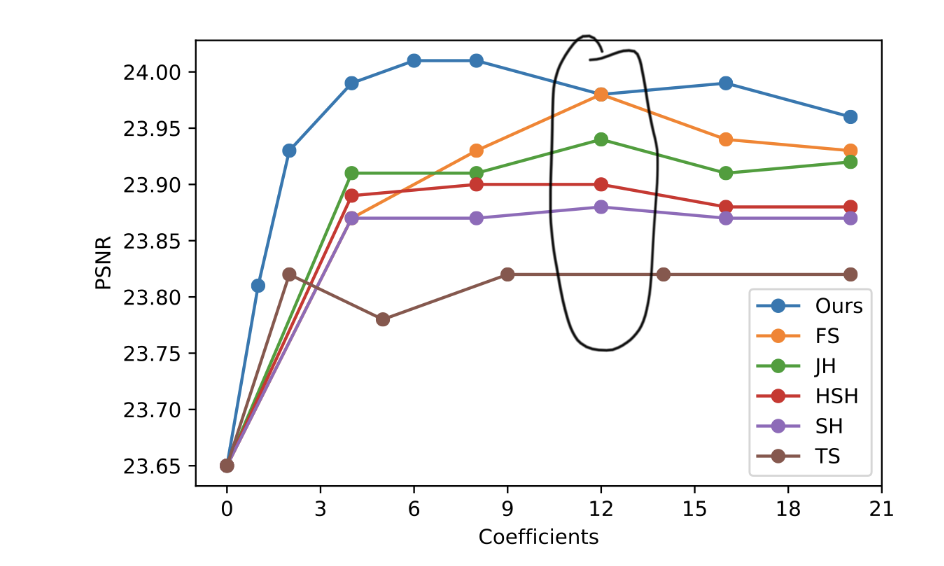
Author has also evaluated learned basis function instead of fixed ones: FS (Fourier’s series), JH (Jacobi spherical harmonics), HSH (hemispherical harmonics), SH (spherical harmonics), and TS (Taylor’s series). The comparison on different number (n) of basis function are also evaluated. The figure below indicates 12 basis seems to be sufficient.
Experiment Result
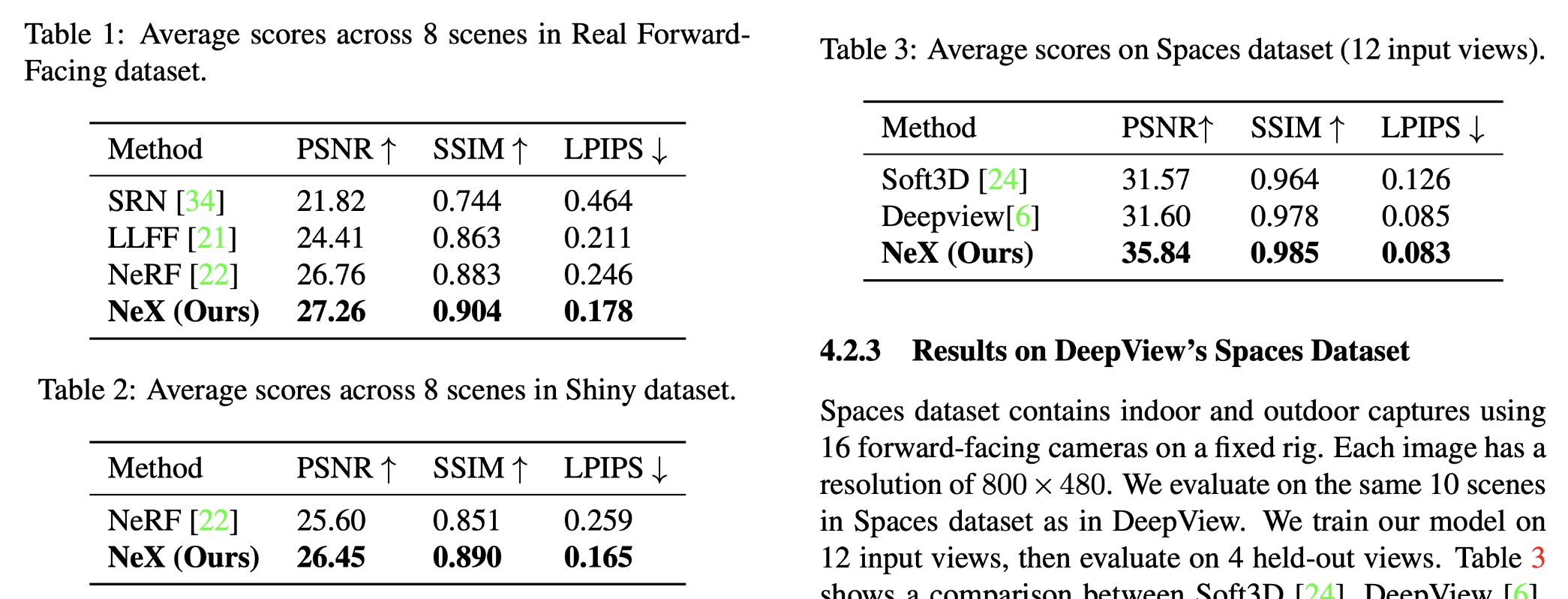
The proposed method has been compared to several state of art methods on three datasets on three metrics and the result is shown as below.
Here are some visual examples. It is obvious that the proposed method’s output is more sharp and reserves more details.


