When Noisy Labels Meet Long Tail Dilemmas A Representation Calibration Method
[calibration data-balance noisy dataset deep-learning long-tail co-teaching This is my reading note for When Noisy Labels Meet Long Tail Dilemmas: A Representation Calibration Method. The paper proposes a method to train model from a dataset contains long tail and noisy labels . It’s based on contrast learning to learn a robust representation of data; then clustering process is applied to recover the true labels.
Introduction
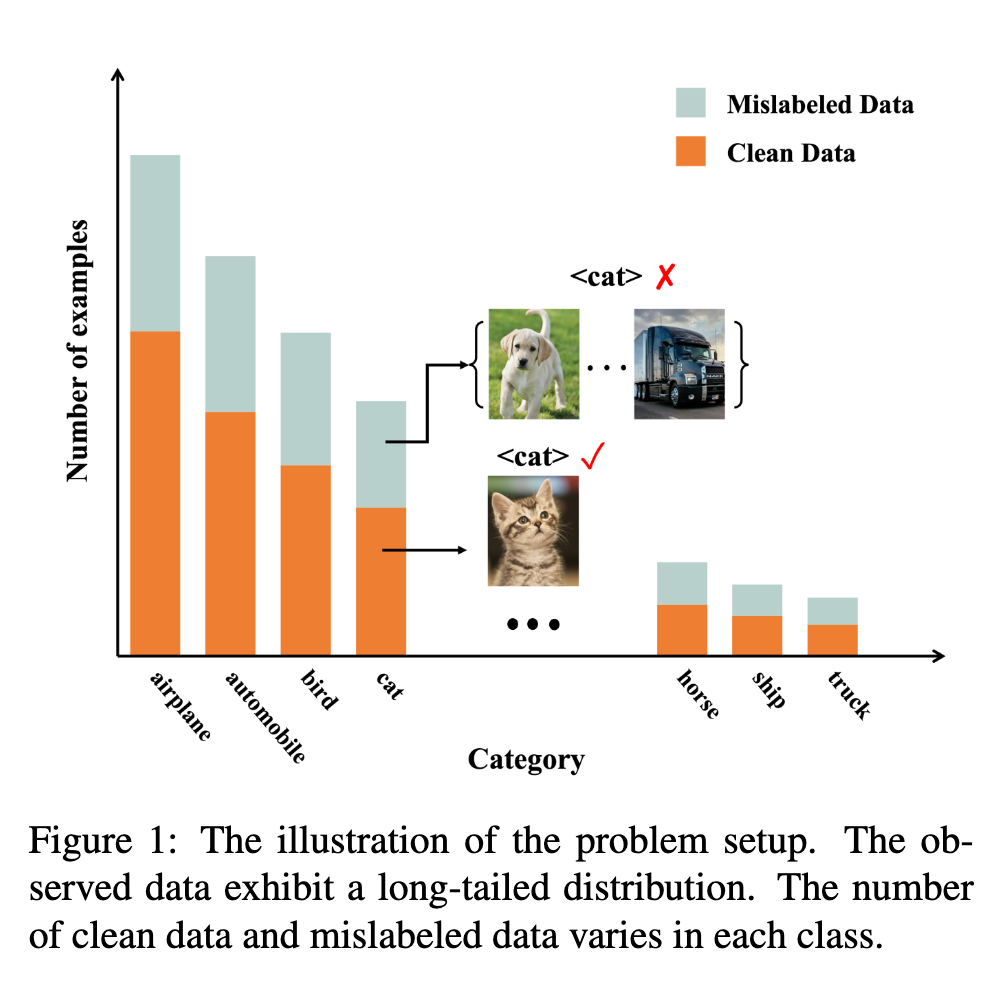
It is hence significant to address the simultaneous incorrect labeling and class-imbalance, i.e., the problem of learning with noisy labels on long-tailed data. We propose a representation calibration method RCAL. Specifically, RCAL works with the representations extracted by unsupervised contrastive learning. We assume that without incorrect labeling and class imbalance, the representations of instances in each class conform to a multivariate Gaussian distribution, which is much milder and easier to be checked. Based on the assumption, we recover underlying representation distributions from polluted ones resulting from mislabeled and class-imbalanced data. Additional data points are then sampled from the recovered distributions to help generalization. Moreover, during classifier training, representation learning takes advantage of representation robustness brought by contrastive learning, which further improves the classifier performance (p. 1)
Namely, they are weak for learning with noisy labels on long-tailed data. For example, the popularly used memorization effect [18] for tackling noisy labels cannot be applied, since clean data belonging to tail classes show similar training dynamics to those mislabeled data, e.g., similar training losses [5, 64]. Also, the noise transition matrix used for handling noisy labels cannot be estimated accurately. This results from that the relied anchor points of tail classes cannot be identified from noisy data, as the estimations of noisy class posterior probabilities for tail classes are not accurate. Moreover, the methods specialized for learning with long-tailed data mainly adopt re-sampling and re-weighting techniques to balance the classifier. The side-effect of mislabeled data is not taken into consideration, which results in the accumulation of label errors. (p. 2)
Existing methods targeting this problem can be divided into two main categories. The methods in the first category are to distinguish mislabeled data from the data of tail classes for follow-up procedures. However, the distinguishment is adversely affected by mislabeled data, since the information used for the distinguishment comes from deep networks that are trained on noisy long-tailed data. The methods in the second category are to reduce the side-effects of mislabeled data and long-tailed data in a unified way, which rely on strong assumptions. For example, partial data should have the same aleatoric uncertainty [5], which is hard to check in practice. (p. 2)
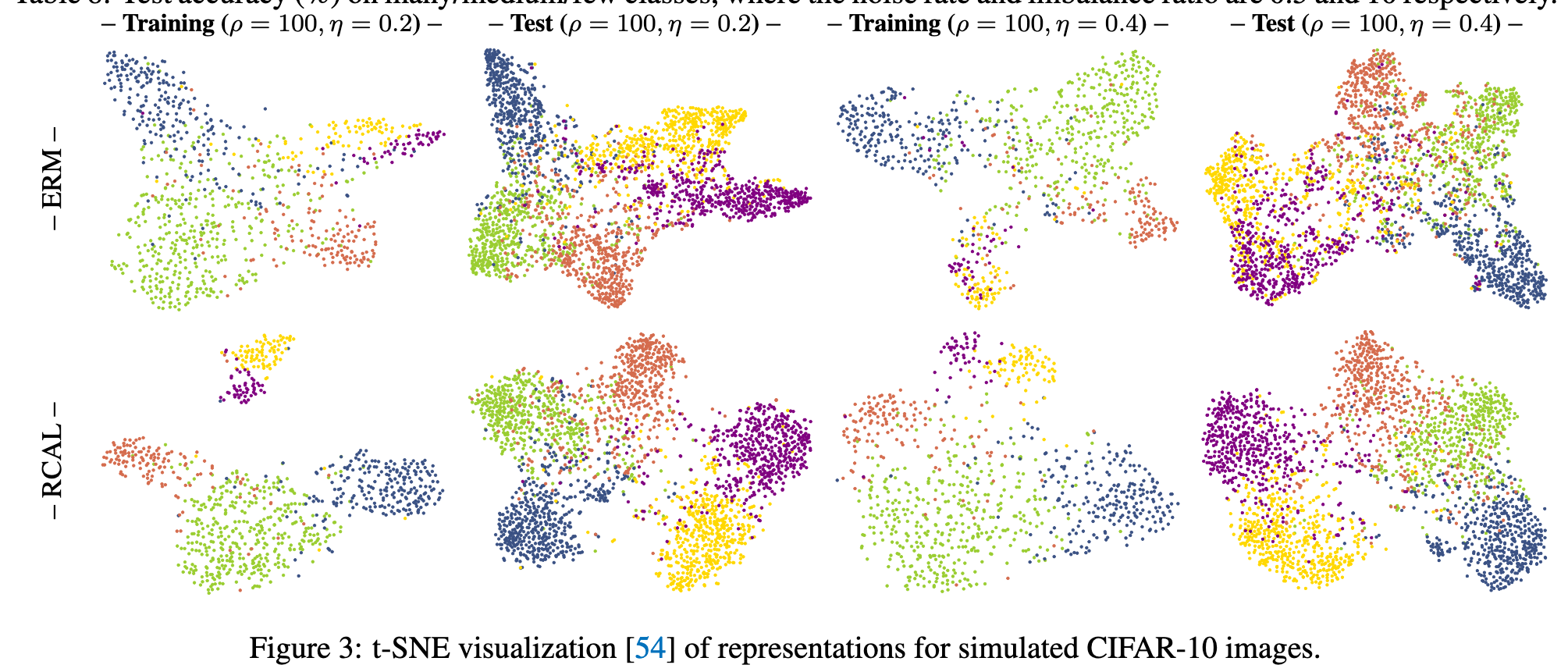
Technically, we first employ unsupervised contrastive learning to achieve representations for all training instances. As the procedure of representation learning is not influenced by corrupted training labels, the achieved representations are naturally robust [81, 69, 15]. Afterward, based upon the achieved representations, two representation calibration strategies are performed: distributional and individual representation calibrations. (p. 2)
In more detail, the distributional representation calibration aims to recover representation distributions before data corruption. Specifically, we assume that before training data are corrupted, the deep representations of instances in each class conform to a multivariate Gaussian distribution. (p. 2)
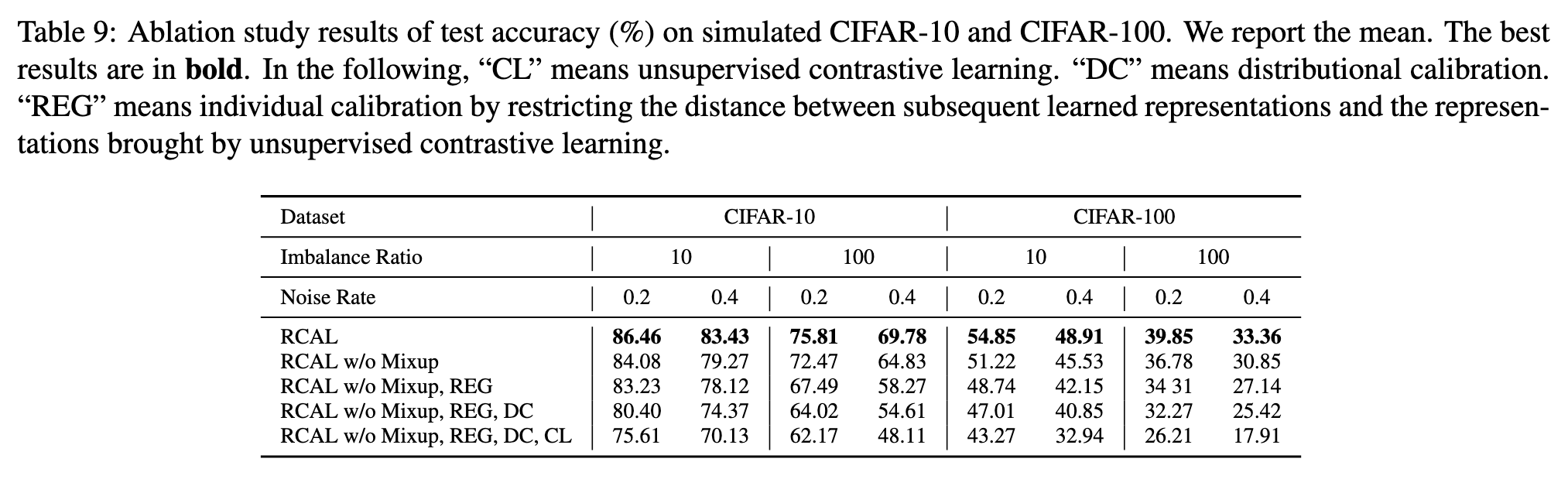
Moreover, since the in sufficient data of tail classes may cause biased distribution estimations, the statistics of distributions from head classes are employed to calibrate the estimations for tail classes. After the distributional calibration for all classes, we sample multiple data points from the recovered distributions, which makes training data more balanced and helps generalization1. As for individual representation calibration, considering that the representations obtained by contrastive learning are robust, we restrict that the subsequent learned representations during training are close to them. The individual representation calibration implicitly reduces the hypothesis space of deep networks, which mitigates their overfitting of mislabeled and long-tailed data. (p. 2)
Related Works
Learning with Noisy Labels
There is a series of works proposed to deal with noisy labels, which includes but do not limit to estimating the noise transition matrix [65, 10, 72], selecting confident examples [49, 59, 47], reweighting examples [50, 43], and correcting wrong labels [41]. Additionally, some stateof-the-art methods combine multiple techniques, e.g., DivideMix [32], ELR+ [42], and Sel-CL+ [34]. (p. 2)
Learning with Long-tailed Data
Existing methods tackling long-tailed data mainly focus on: (1) re-balancing data distributions, such as oversampling [17, 4, 49], under-sampling [13, 4, 19], and class-balanced sampling [46, 51]; (2) re-designing loss functions, which includes class-level re-weighting [11, 6, 23, 31, 57, 56] and instance-level re-weighting [38, 52, 50, 80]; (3) decoupling representation learning and classifier learning [27, 76]; (4) transfer learning from head knowledge to tail classes [24, 39, 22]. (p. 3)
Learning with Noisy Labels on Long-tailed Data
A line of research has made progress towards simultaneously learning with imbalanced data and noisy labels. CurveNet [26] exploits the informative loss curve to identify different biased data types and produces proper example weights in a meta-learning manner, where a small additional unbiased data set is required. HAR [5] proposes a heteroskedastic adaptive regularization approach to handle the joint problem in a unified way. The examples with high uncertainty and low density will be assigned larger regularization strengths. RoLT [61] claims the failure of the smallloss trick in long-tailed learning and designs a prototypical error detection method to better differentiate the mislabeled examples from rare examples. TBSS [77] designs two metrics to detect mislabeled examples under long-tailed data distribution. A semi-supervised technique is then applied. (p. 3)
Methodology
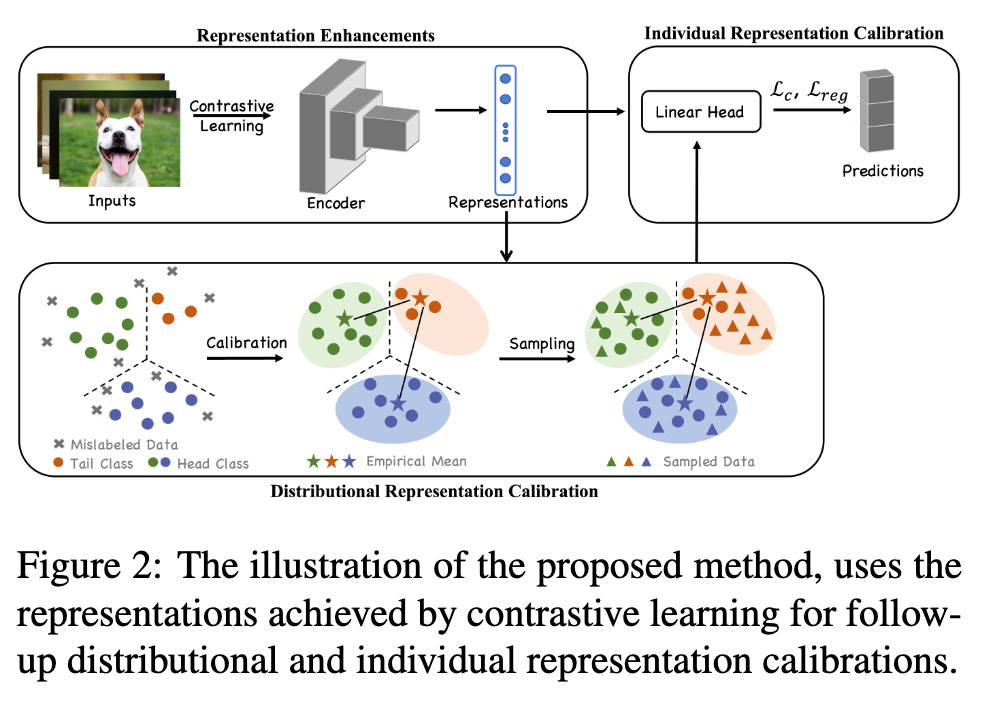
Enhancing Representations by Contrastive Learning
Specifically, we utilize the encoder networks following the popular setup in MOCO [9]. For an input x, we apply two random augmentations and thus generate two views xq and xk. The two views are then fed into a query encoder f(·) and a key encoder f′(·), which generates representations zq = f(xq) and zk = f′(xk). Thereafter, a projection head, i.e., a 2-layer MLP, maps the two representations to lower-dimensional embeddings zˆq and zˆk. MOCO also maintains a large queue to learn good representations. The key encoder uses a momentum update with the query encoder to keep the queue as consistent as possible. (p. 3)
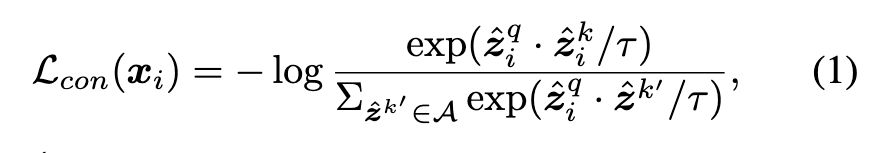
Distributional Representation Calibration
Although without introducing class labels in representation learning by contrastive learning, there is a clustering effect for the obtained representations [81]. Therefore, we can exploit them for modeling the multivariate Gaussian distributions at a class level. Due to the side-effect of mislabeled data, the prior multivariate Gaussian distributions are corrupted. As mentioned, we tend to tackle noisy labels in long-tailed cases, with representation distribution calibration. Therefore, we need to estimate the multivariate Gaussian distributions that are not affected by mislabeled data. (p. 4)
Robust estimations of Gaussian distributions
Technically, given the learned representations z, we employ the Local Outlier Factor (LOF) algorithm [3] to detect outliers. The outliers are then removed for the following estimation. (p. 4)
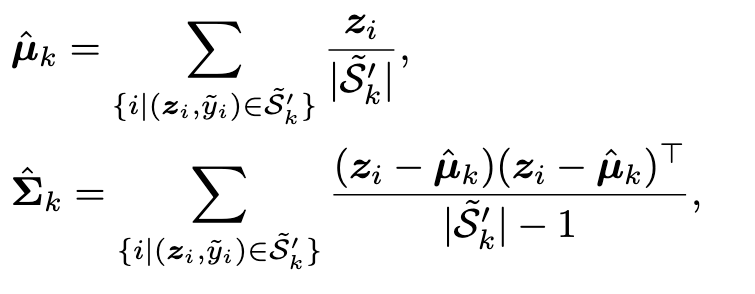
Further calibration for tail classes
As the size of the training data belonging to tail classes is small, it may not be enough for accurately estimating their multivariate Gaussian distributions with the above robust estimation. Inspired by similar classes having similar means and covariance on representations [70, 55], we further borrow the statistics of head classes to assist the calibration of tail classes. Specifically, we measure the similarity by computing the Euclidean distances between the means of representations of different classes. For the tail class k, we select top q head classes with the closest Euclidean distance to the mean µˆk (p. 4)
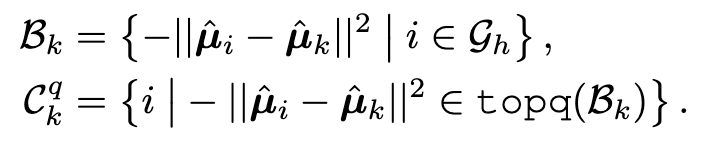
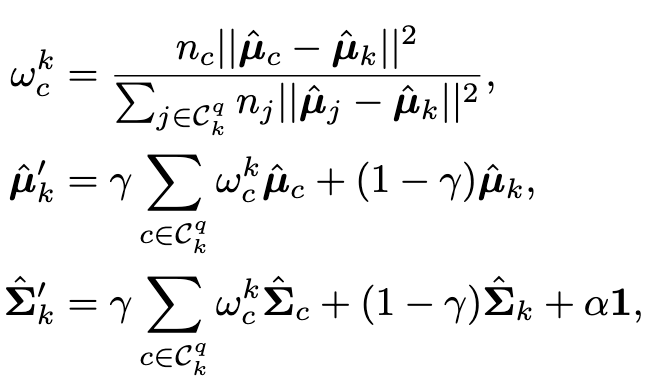
Individual Representation Calibration
we restrict the distance between subsequent learned representations and the representations brought by contrastive learning. (p. 5)
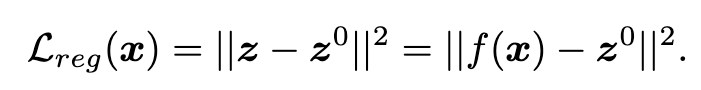
Second, to further make learned representations robust to tackle noisy labels in long-tailed cases, we employ the mixup method [74]. (p. 5)
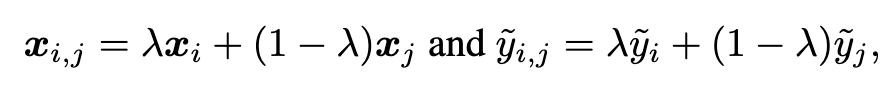
Theoretical Analysis
Assumption 3.1. (1) (Gaussian deep representations) The m-dimensional representation z and the corresponding true label y satisfies P(y = k) = n_k/n and z | y = k ∼ N (µ_k, Σ). (2) (Class imbalance) There is a constant ρ > 1 such that n_head ≥ ρ · n_tail. (3) (Random label flipping) There is a constant η > 0 such that given the true label y_i = k, the contaminated label y˜i satisfies P(˜y_i = j | y = k) = η · n_j/n for j ̸= k. (4) (Informative head classes) There is a constant δ_q (depending on q) such that $\mbox{max}{j\in C^q_k} \lVert µ_j − µ_k\rVert \leq δ_q$. (p. 5)

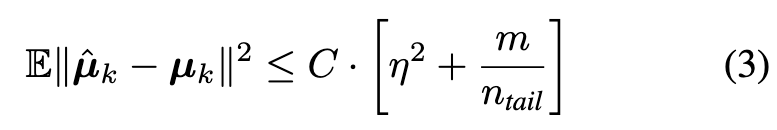
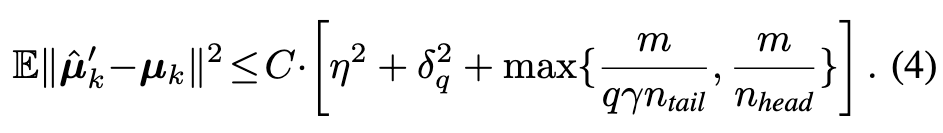
Experiments
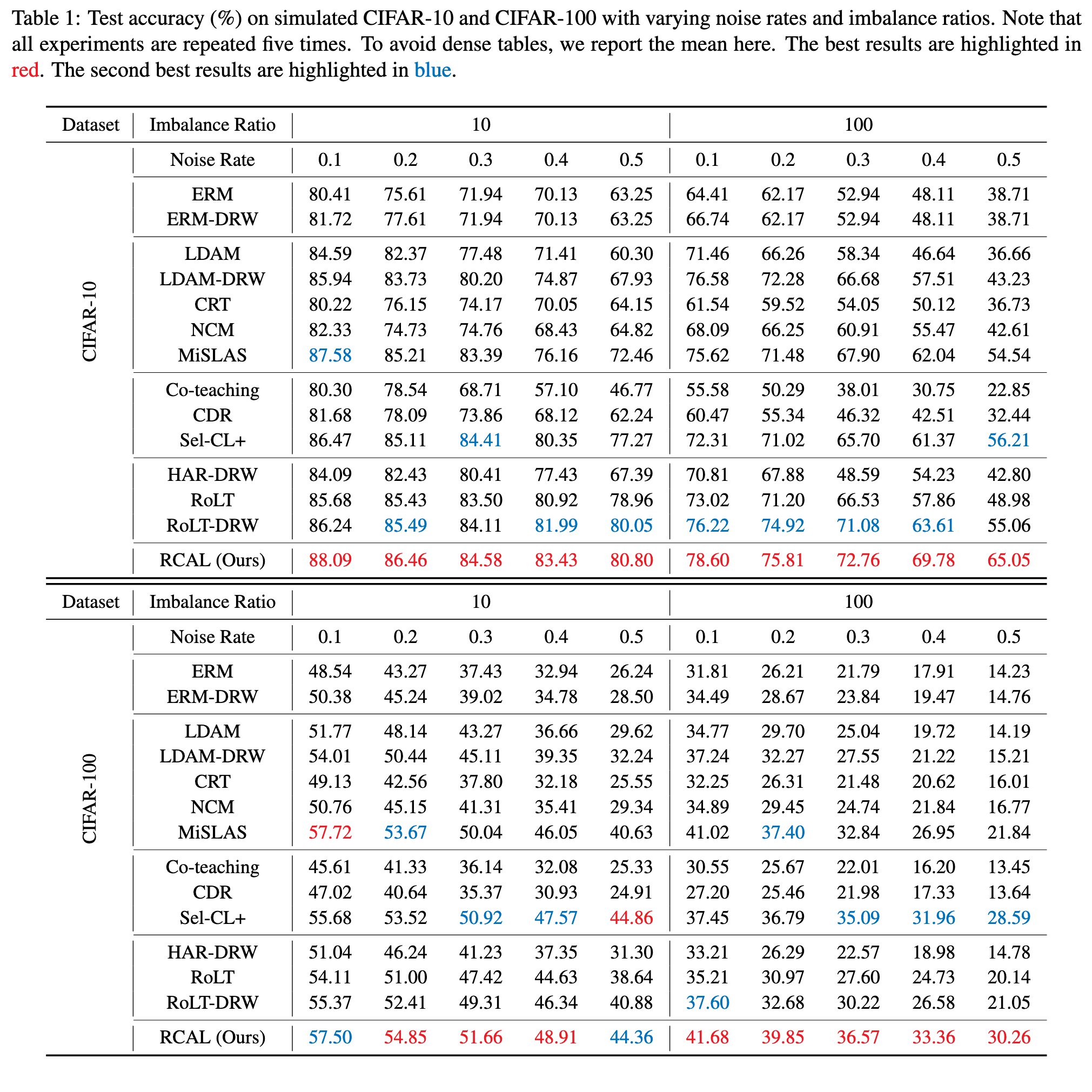
For both CIFAR-10 and CIFAR-100 datasets, we use a ResNet-32 [21] network. We perform the strong augmentations SimAug [8] in the contrastive learning stage and standard weak augmentations in the classifier learning stage. (p. 6)
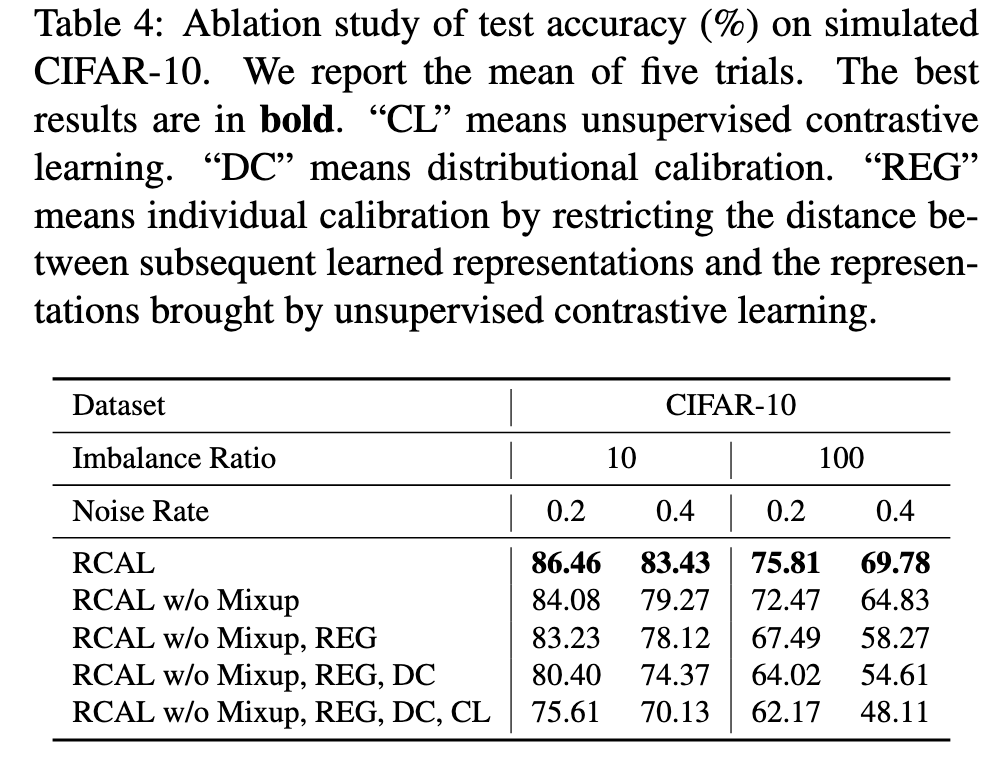
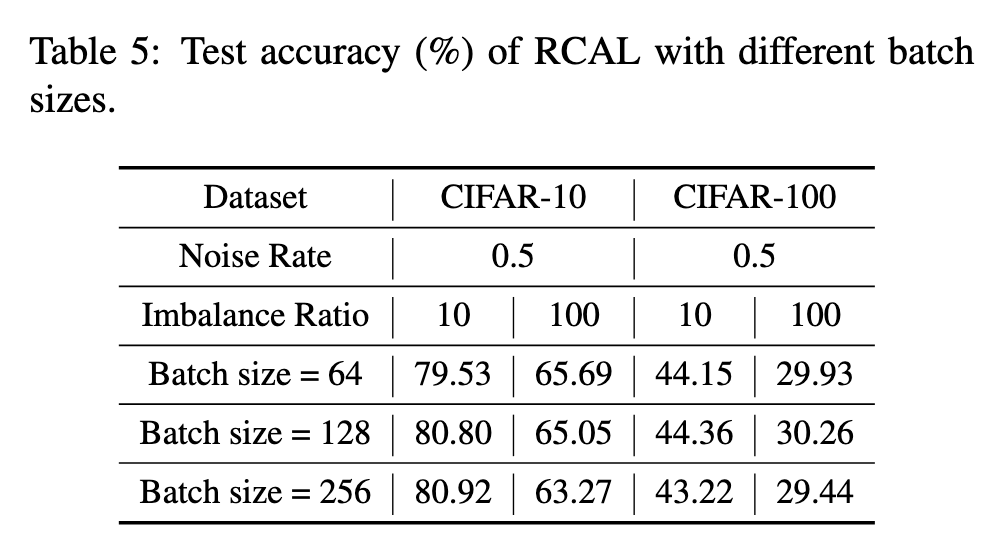
Ablation Study
Fine-grained results and analysis
As can be seen, compared with CE, both MiSLAS can improve the performance on Medium and Few classes, leading to final better overall performance. However, compared with our RCAL, MiSLAS overemphasizes the model performance on Few classes, but somewhat ignores the performance on Many and Medium that also are important. Therefore, as for overall performance, our RCAL surpasses MiSLAS with a clear margin. (p. 9)