ResNet and Its Variations
[shortcut activation deep-learning resnet pre-activation post-activation ResNet
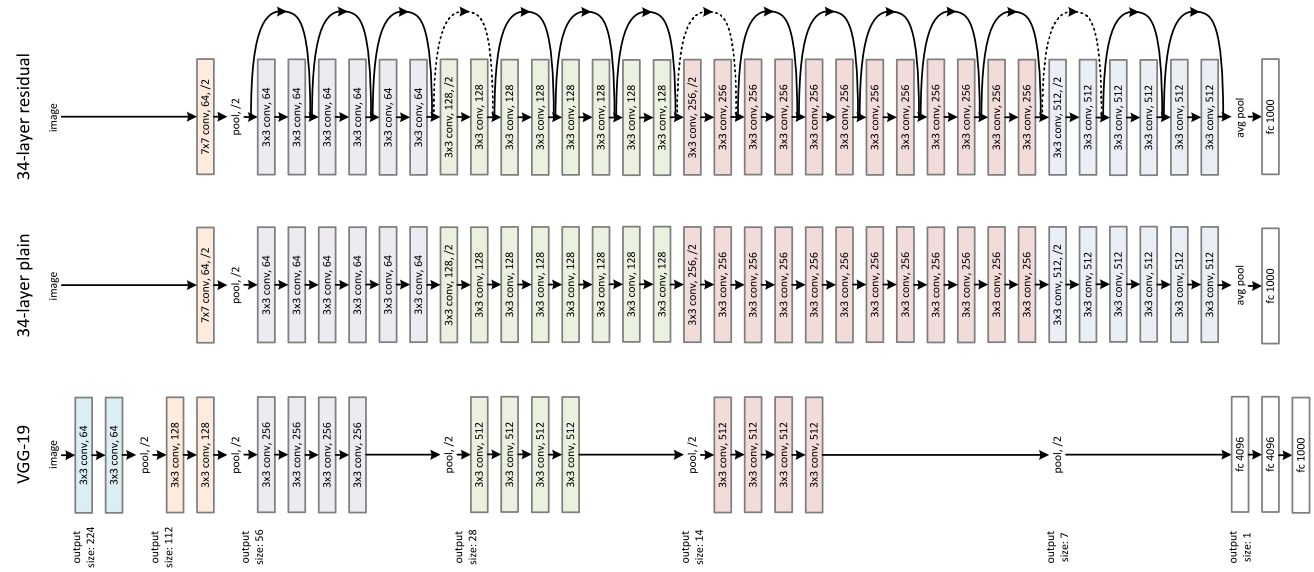
Since proposed in 2016, ResNet has drawn a lot of interests, especially its capabability of training a very deep nerual network (from 19 of VGG19 to 50 or even 200 layers). The magic comes from the residual functions.
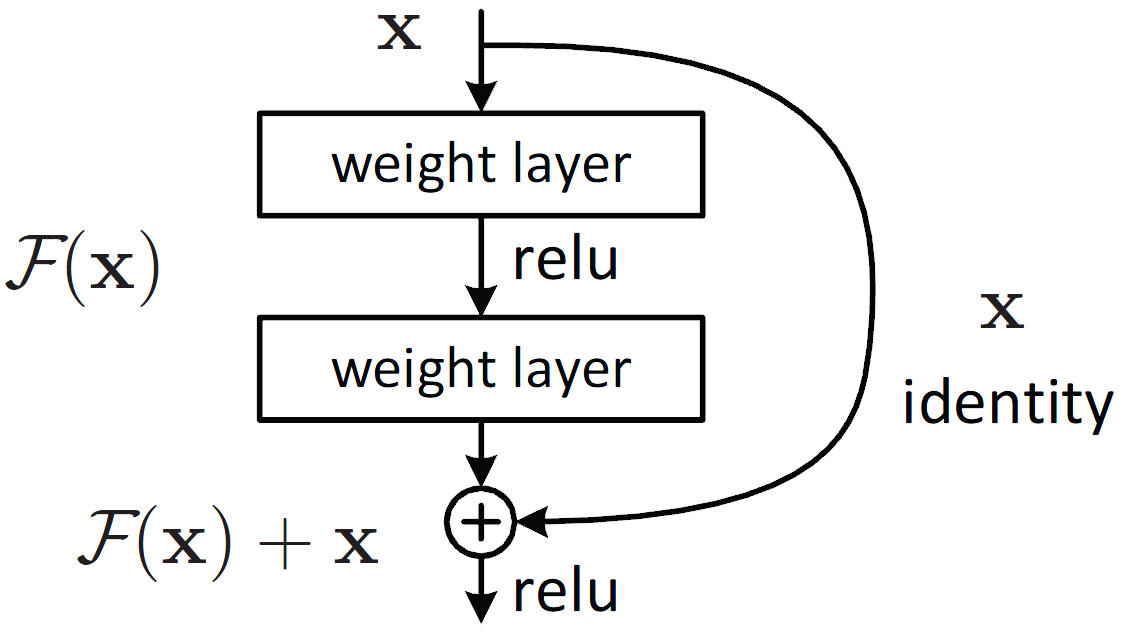
With residual function, the output of layer $l+1$ can be written as:
\(x_{l+1} = f(x_l) + x_l\)
where f represents the function of $l_th$ layer.
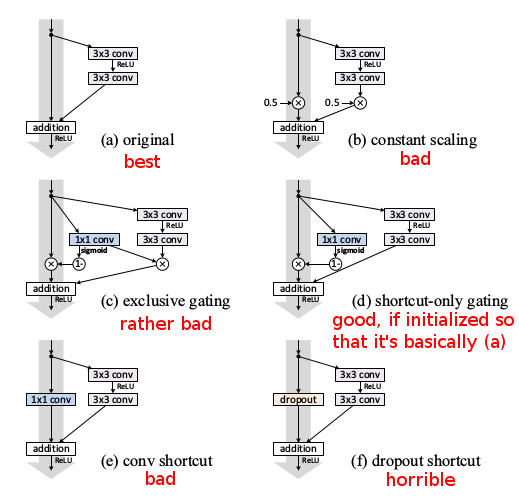
ResNet V2
The difference between the V1 and V2 is (as illustrated below):
- V1: Convolution then batch normalization then ReLU
- V2: Batch normalization then ReLu then convolution
The motivation behind is that V2 is much easier to train and generalizes better than the V1 ResNet

In fact, other variations has been explored as well and obviously not all variations work:

ResNext
Aggregated Residual Transformations for Deep Neural Networks
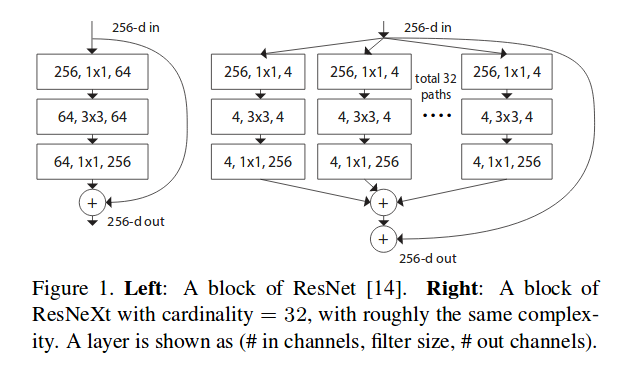
ResNext combines ResNet with split-transform-merge strategy. A module in the network performs a set of transformations, each on a low-dimensional embedding, whose outputs are aggregated by summation.
This Network-in-Neuron can be understood as the boosting, which combines a set of simpler classifier into a powerful one. It also shares the same idea as group-wise convolution as MobileNet.

DenseNet
DenseNet addresses the gradient vanish problem in a different way compared with ResNet: ResNet using sum to combine the output of previous layer and output of current layer as the input of next layer; DenseNet using concatenation to combine the outputs of different layers. In a dense block of DenseNet, the input of layer is the concatnation of outputs of ALL previous layers.

It alleviates the vanishing-gradient problem, strengthen feature propagation, encourage fea- ture reuse, and substantially reduce the number of parameters. The reason for less parameters is that, with dense net narrower filters can be used (less output channels).
Since the number of input channels increase quadratically with regards to layer within the dense block, a bottleneck layer is introduced to reduce the number of feature channels, which is essentially convolution layer with $1\times 1$ kernel size and less output channels than input ones.

