RingNet-Learning to Regress 3D Face Shape and Expression from an Image without 3D Supervision
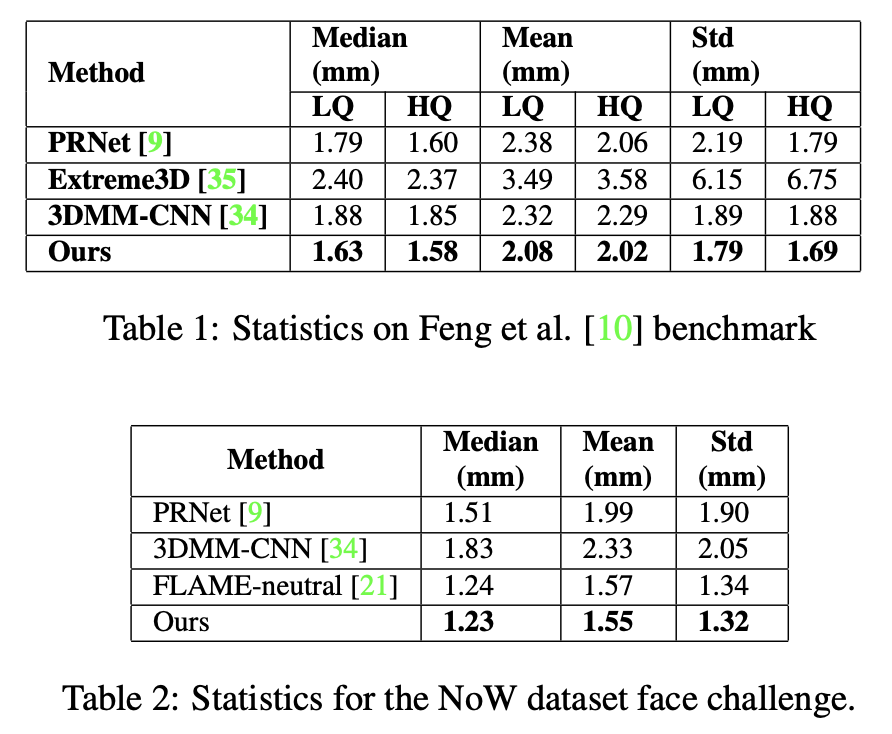
[ringnet flame deep-learning encoder-decoder no-3d consistency 3d This is my reading note for Learning to Regress 3D Face Shape and Expression from an Image without 3D Supervision (code). The paper is also called RingNet and was published in CVPR 2019. The paper solves the problems of 3D face reconstruction from a single 2D image and the training requires no 3D ground truth. To this end, RingNet leverages multiple images of a person and automatically detected 2D face features. It uses a novel loss that encourages the face shape to be similar when the identity is the same and different for different people. This is based on observation that an individual’s face shape is constant across images, regardless of expres- sion, pose, lighting, etc.
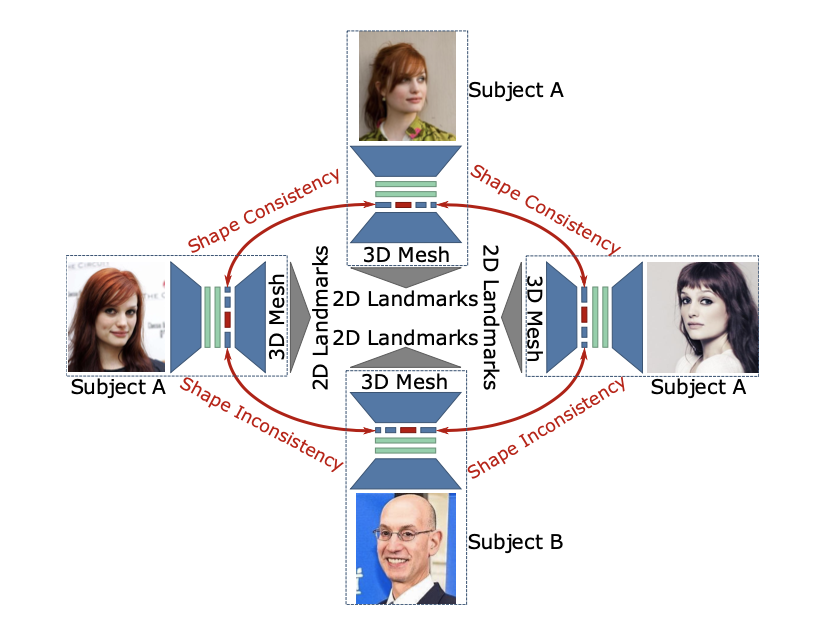
The proposed method is described as figure above. For input, we assume the face is detected, loosely cropped, and approximately centered. During training, our method leverages 68 2D landmarks and identity labels as input. During inference it uses only image pixels; 2D landmarks and identity labels are not used.
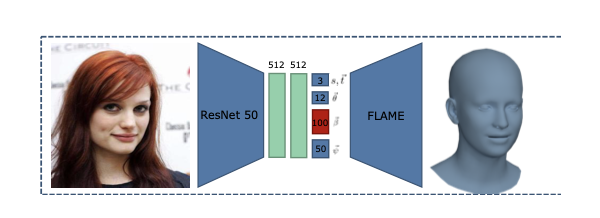
FLAME
FLAME is used as decoder here, which takes feature vectors (identity \(\beta\in\mathbb{R}^{100}\), expression \(\psi\in\mathbb{R}^{50}\) and head pose \(\theta\in\mathbb{R}^{15}\)) as input and generates a face mesh. FLAME also supports different rendering to output the 2D image. FLAME could be written as:
\[M(\beta,\theta,\psi)=W(T+B_S(\beta,S)+B_p(\theta,P)+B_E(\psi,E),J(\beta),\theta)\]FLAME’s parameter is fixed in RingNet.
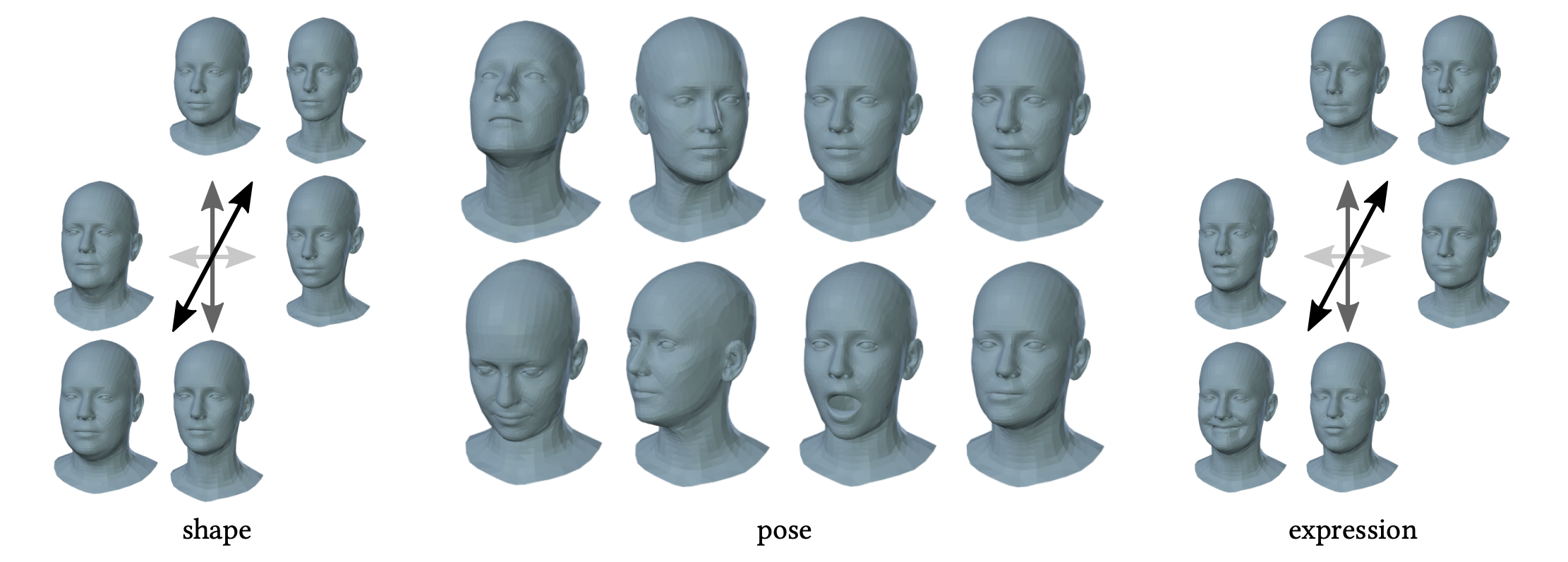
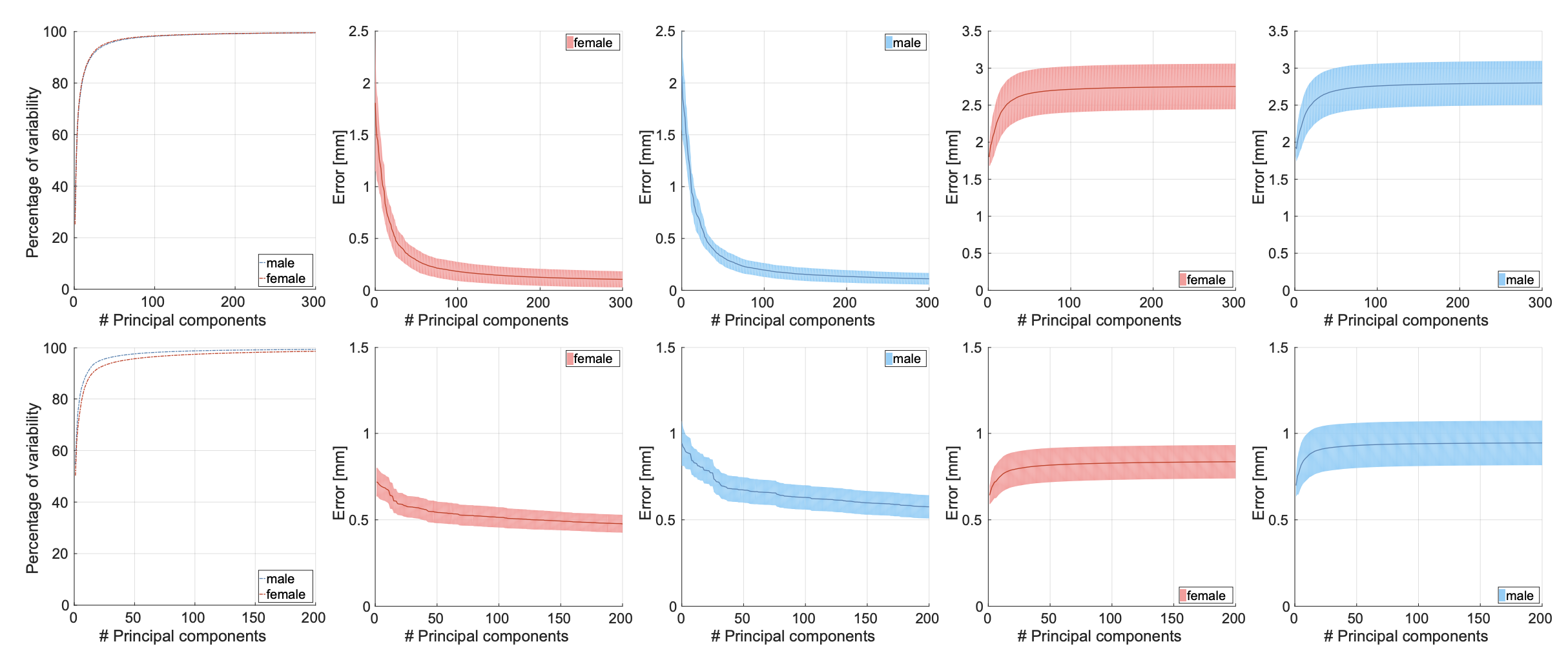
This figure shows the coverage of variability given different number of basis.
Encoder
The encoder of RingNet incldues a feature extraction network, which is ResNet50, and regression network. Feature extraction network outputs a feature vector of 2048 elements. The regression network consists of two fully-connected layers of dimension 512 with ReLu activation and dropout, followed by a final linear fully-connected layer with 159-dimensional output. The 159-dimension output is then used input to the FLAME.
Shape Consistency Loss
RingNet contains R (R=6 in the paper) of such encoder-decoder networks, where encoder’s weights are shared and decoder weights are fixed. For those R networks, R-1 takes images from same subject and the last one takes image from a different subject. The key idea here is that RingNet the identity shape for R-1 images from the same subject should be similar to each other; while being different from the identity shape for the last image, as it is from different subject. To this end shape consistency loss is used.
\[\ell_{sc}=\sum_{i=1}^{n_b}{\sum_{j,k=1}^{R-1}{\max(0,\lVert\beta_{i,j}-\beta_{i,k}\rVert_2^2-\lVert \beta_{i,j}-\beta_{i,R}\rVert_2^2+\eta)}}\]Here \(\eta\) is the margin required for distance between identity shape of images from the same subject to the identity shape of images of a different subject.
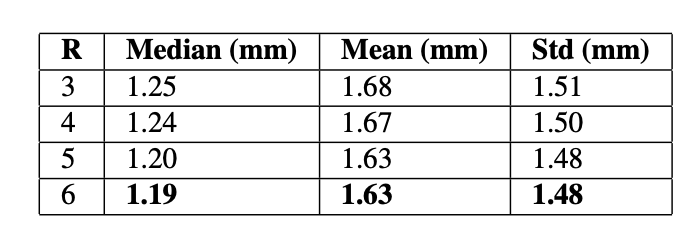
The impact of R is shown in the table below:
2D Feature Loss
L1 loss between the ground-truth landmarks provided during the training procedure and the predicted landmarks is also used to ensure the geometry correctness of 3D face.
Two types of landmarks are considered:
- the mouth, nose, eye, and eyebrow key-points have a fixed corresponding 3D point (referred to as static 3D landmarks)
- the position of the contour features changes with head pose (referred to as dynamic 3D landmarks)
we model the contour landmarks as dynamically moving with the global head rotation (see Sup. Mat.). To automatically compute this dynamic contour, we rotate the FLAME template between -20 and 40 degrees to the left and right, render the mesh with texture, run OpenPose to predict 2D landmarks, and project these 2D points to the 3D surface. The resulting trajectories are symmetrically transferred between the left and right side of the face.
The 2D feature loss could be written as below and \(w_i\) is the confidence score of each ground-truth land- mark which is provided by the 2D landmark predictor.
\[\ell_{proj}\lVert w_i\times(k_{p_i}-k_i)\rVert\]RingNet
Finally the loss for the whole RingNet could be written as:
\[\ell=\lambda_{sc}\ell_{sc}+\lambda_{proj}\ell_{proj}+\lambda_\beta\lVert\beta\rVert_2^2+\lambda_\psi\lVert\psi\rVert_2^2\]The paper used the following parameter R = 6, \(\lambda_{SC} = 1\), \(\lambda_{proj} = 60\), \(\lambda_\beta =1e−4\),\(\lambda_\psi =1e−4\),\(\eta=0.5\). RingNet is trained for 10 epochs with a constant learning rate of 1e-4, and use Adam for optimization. The experiment result is shown as table below: