Small-scale proxies for large-scale Transformer training instabilities
[vit layer-norm stability deep-learning review transformer This is my reading note for Small-scale proxies for large-scale Transformer training instabilities. This paper discusses the method to improve model training stability related to hyper parameter.
Introduction
Teams that have trained large Transformer-based models have reported training instabilities at large scale that did not appear when training with the same hyperparameters at smaller scales. (p. 1)
First, we focus on two sources of training instability described in previous work: the growth of logits in attention layers (Dehghani et al., 2023) and divergence of the output logits from the log probabilities (Chowdhery et al., 2022). By measuring the relationship between learning rate and loss across scales, we show that these instabilities also appear in small models when training at high learning rates, and that mitigations previously employed at large scales are equally effective in this regime. This prompts us to investigate the extent to which other known optimizer and model interventions influence the sensitivity of the final loss to changes in the learning rate. To this end, we study methods such as warm-up, weight decay, and the µParam (Yang et al., 2022), and combine techniques to train small models that achieve similar losses across orders of magnitude of learning rate variation. (p. 1)
Experimental methodology
By default, we use AdamW [33] with β_1 = 0.9, β_2 = 0.95, ϵ = 1e-8, and gradient clipping at global norm 1. The default warmup is 5e3 steps, and the default number of total steps is 1e5. We use a linear schedule for warmup and and a cosine-decay [32] schedule for the remainder, with minimum learning rate 1e-5. We use an independent weight decay of 1e-4 and auxiliary z-loss [6] with coefficient 1e-4. (p. 2)
We use pre-normalization [38] Transformers with qk-layer norm [11] (see Section 3.1.1 for information). We do not use any biases following Chowdhery et al. [6], and the layer norm [1] ϵ remains at the default value in Flax [20] of 1e-6. (p. 3)
The embedding initialization is the default in Flax, which is normally distributed with standard deviation 1/√d. The remainder of the weights are initialized with a truncated normal distribution with inverse root fan-in standard deviation [18]. The default batch size is 256, where each batch element has a sequence length of 512 tokens. Sequences are packed so that no padding is required. Finally, we use the vocabulary from Raffel et al. [40] which has size 32101 and uses a SentencePiece [28] tokenizer. We train on TPUs [26] in bfloat16 precision using Flax [20] and JAX [4]. (p. 3)
Results
Attention logit growth
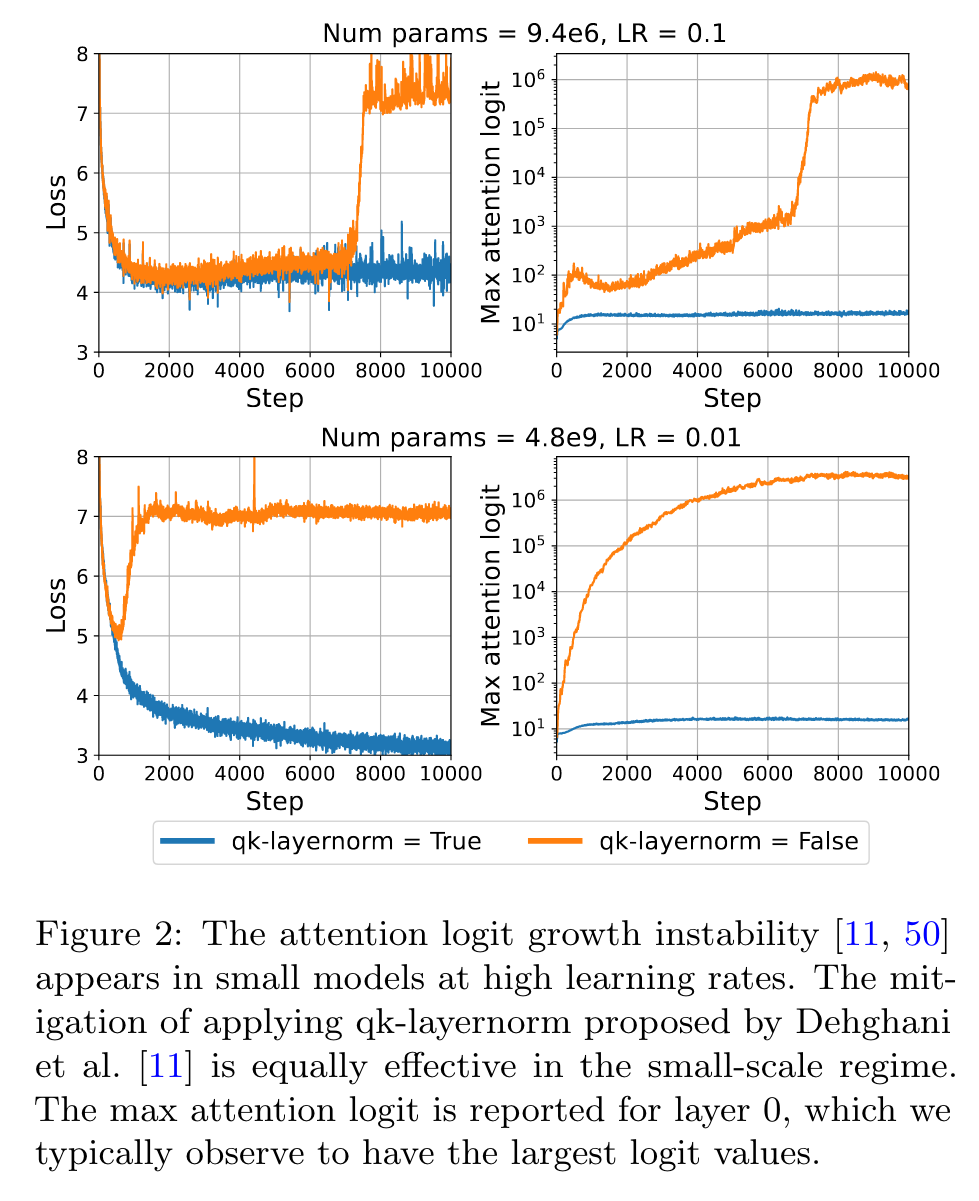
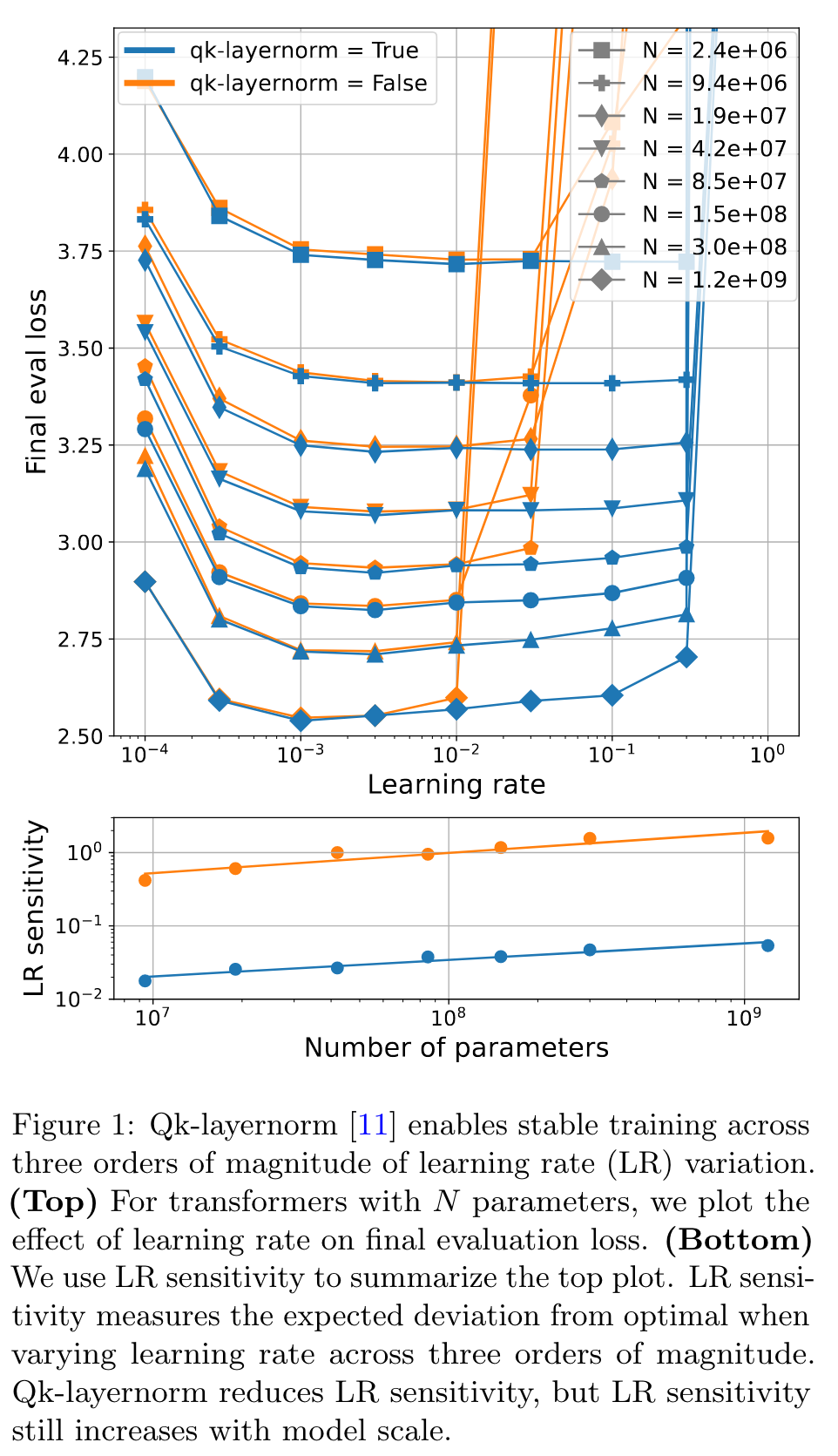
Researchers have previously documented that Transformer training fails when the attention logits become large [11, 50]. (p. 4)
As a result, the attention weights collapse to one-hot vectors, which was named attention entropy collapse by Zhai et al. [50]. To resolve this issue, Dehghani et al. [11] proposed qk-layernorm, which applies LayerNorm [1] to the queries and keys before computing the attention logits. (p. 4)
As a highlight, qk-layernorm allows training a model with 1.2B parameters at learning rate 0.3. Both with and without qk-layernorm, LR sensitivity increases with scale. (p. 4)
Output logit divergence
Let y denote the model’s output logits, which are used to compute class probabilities pi via a softmax p+i = e^{y_i} /Z where Z = \suym_j e^{y_j} . This instability occurs when the logits diverge and become very negative (p. 5)
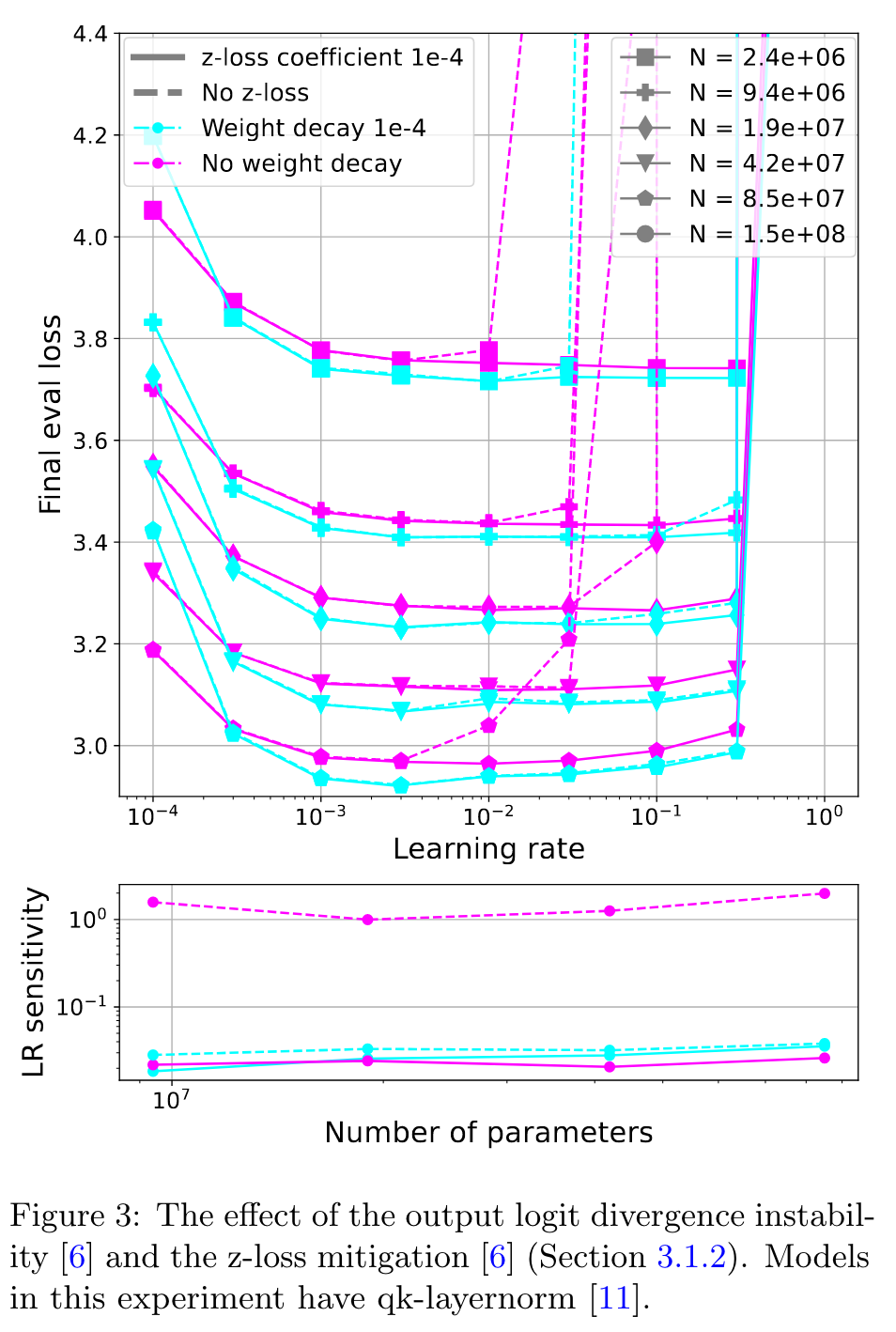
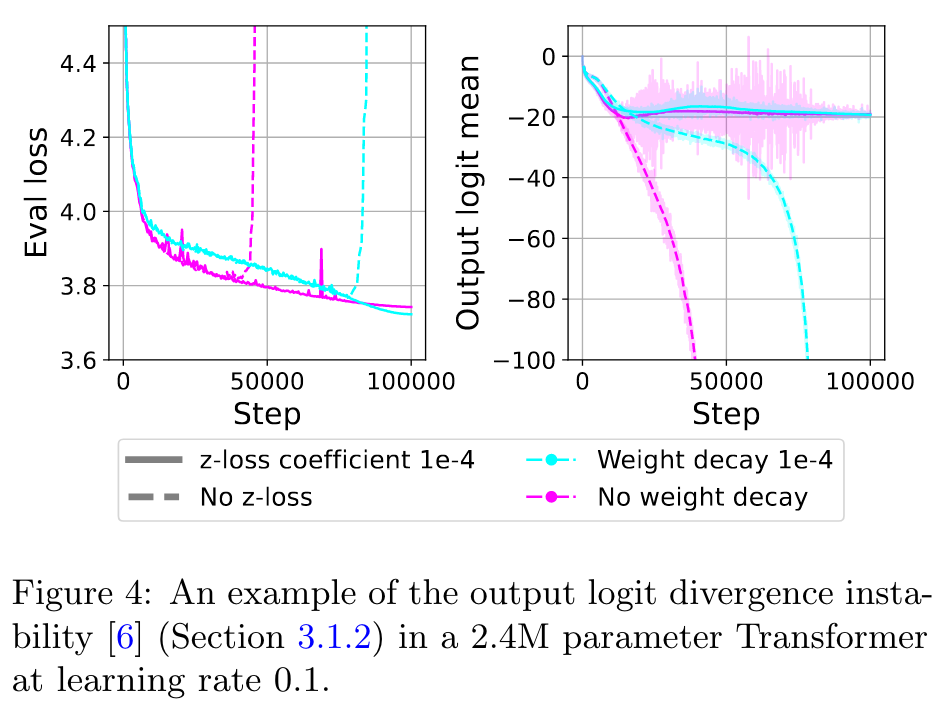
In contrast to the attention logit growth instability, this divergence occurs towards the end of training. The mitigation proposed by Chowdhery et al. [6] is to encourage log Z to remain close to zero. They add an auxiliary loss log2 Z, referred to as z-loss, with coefficient 1e-4. (p. 5)
As illustrated in Figures 3 and 4, we find that instability related to output logit divergence occurs in models with no weight decay regardless of scale, and z-loss resolves this instability. Weight decay also mitigates this instability for the larger models we test (p. 5)
Warm-up
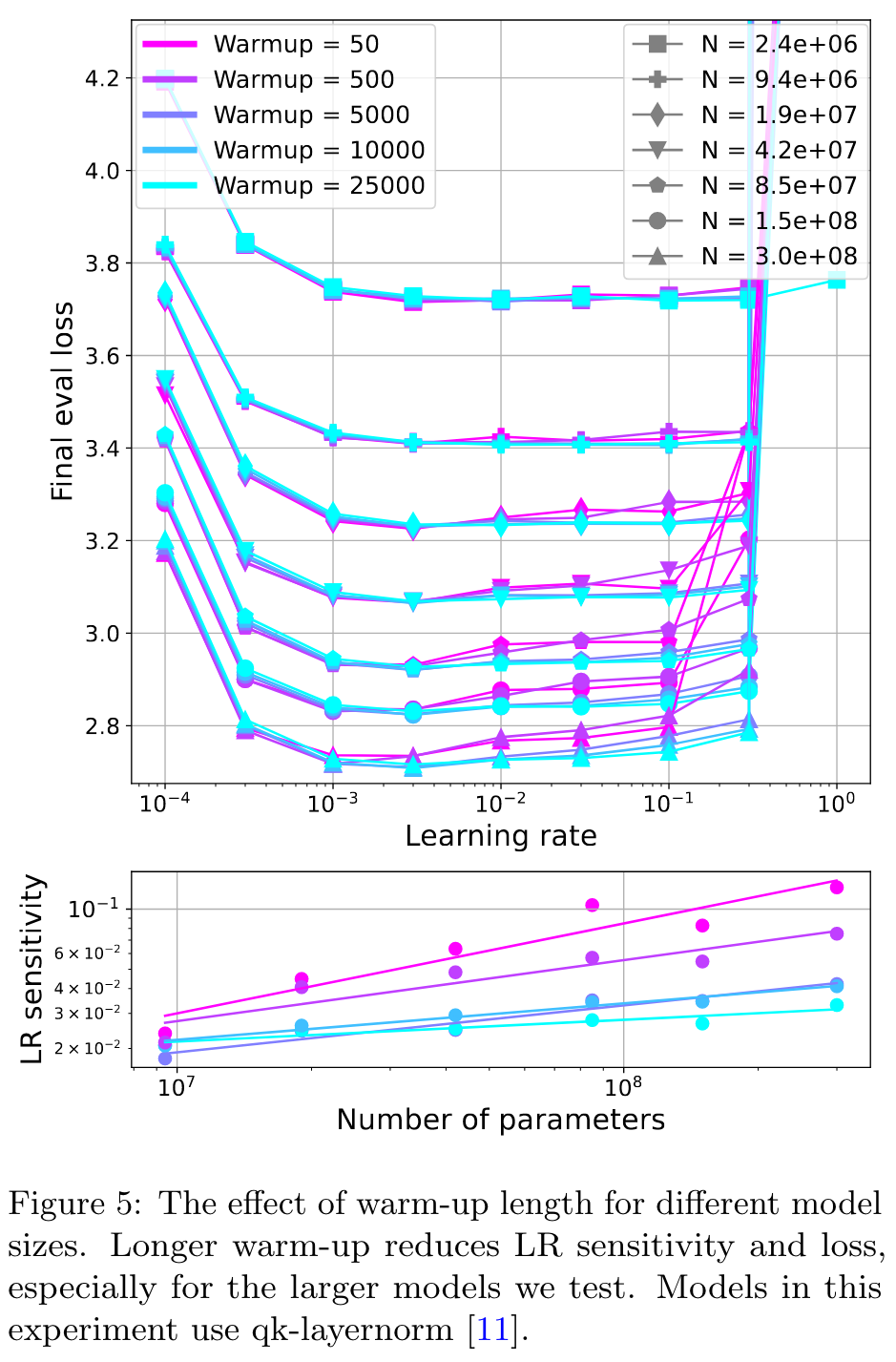
As illustrated by Figure 5, a longer warm-up period reduces LR sensitivity. This is most clear for the larger models, which are not stable at LR 3e-1 without long warm-up. (p. 5)
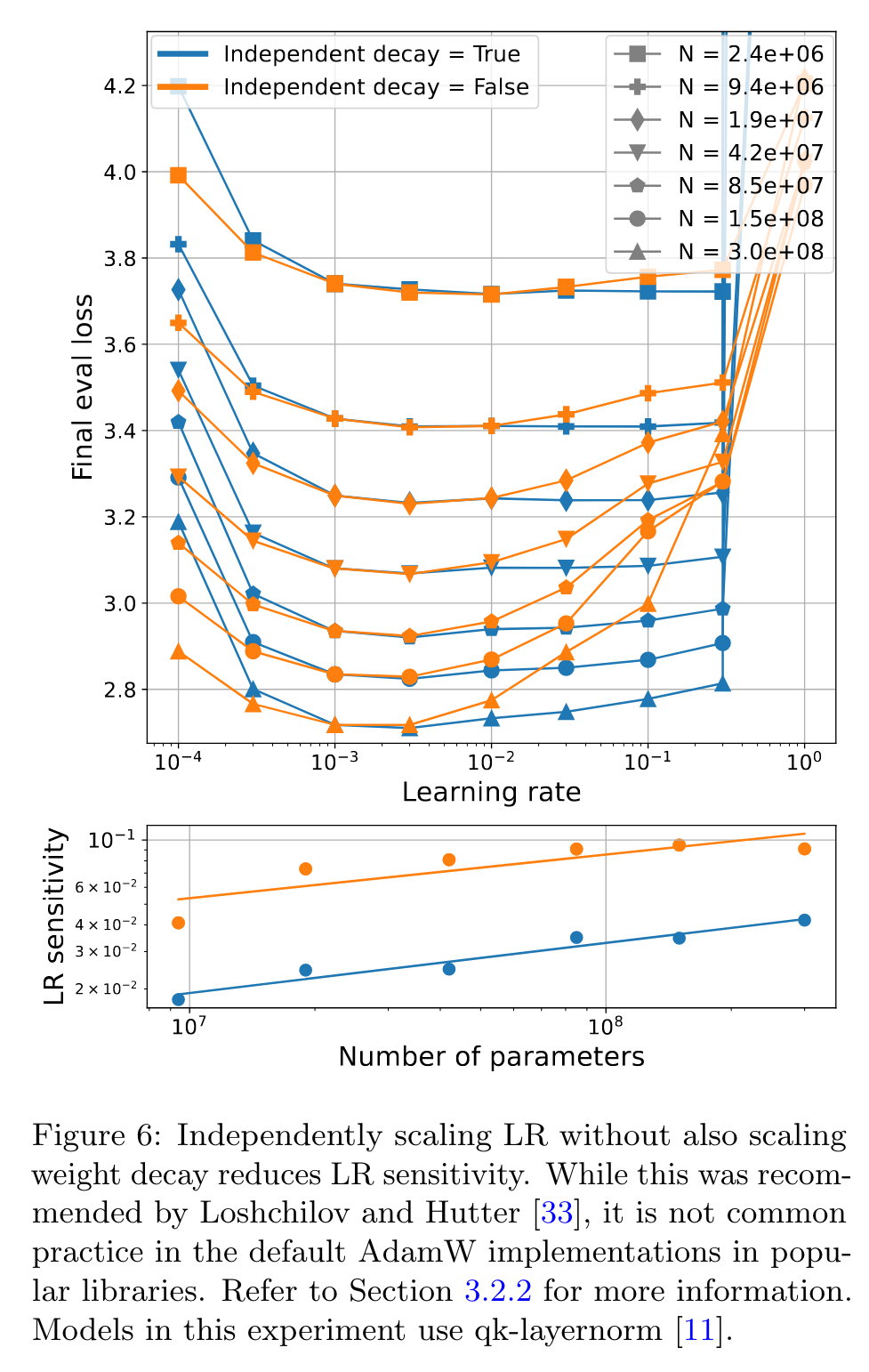
For parameters θ, let ∆ = v/ (√u + ϵ) denote the AdamW update without learning rate or weight decay. For weight decay coefficient λ, max learning rate η, and schedule st ∈ [0, 1], Loshchilov and Hutter [33] recommend the update θ ← θ−st(η∆−λθ), which we refer to as independent decay. On the other hand, the default implementation in PyTorch or Optax applies the update θ ← θ − stη(∆ − λθ), i.e., η now scales both terms. (p. 6)
Scaling width vs. depth
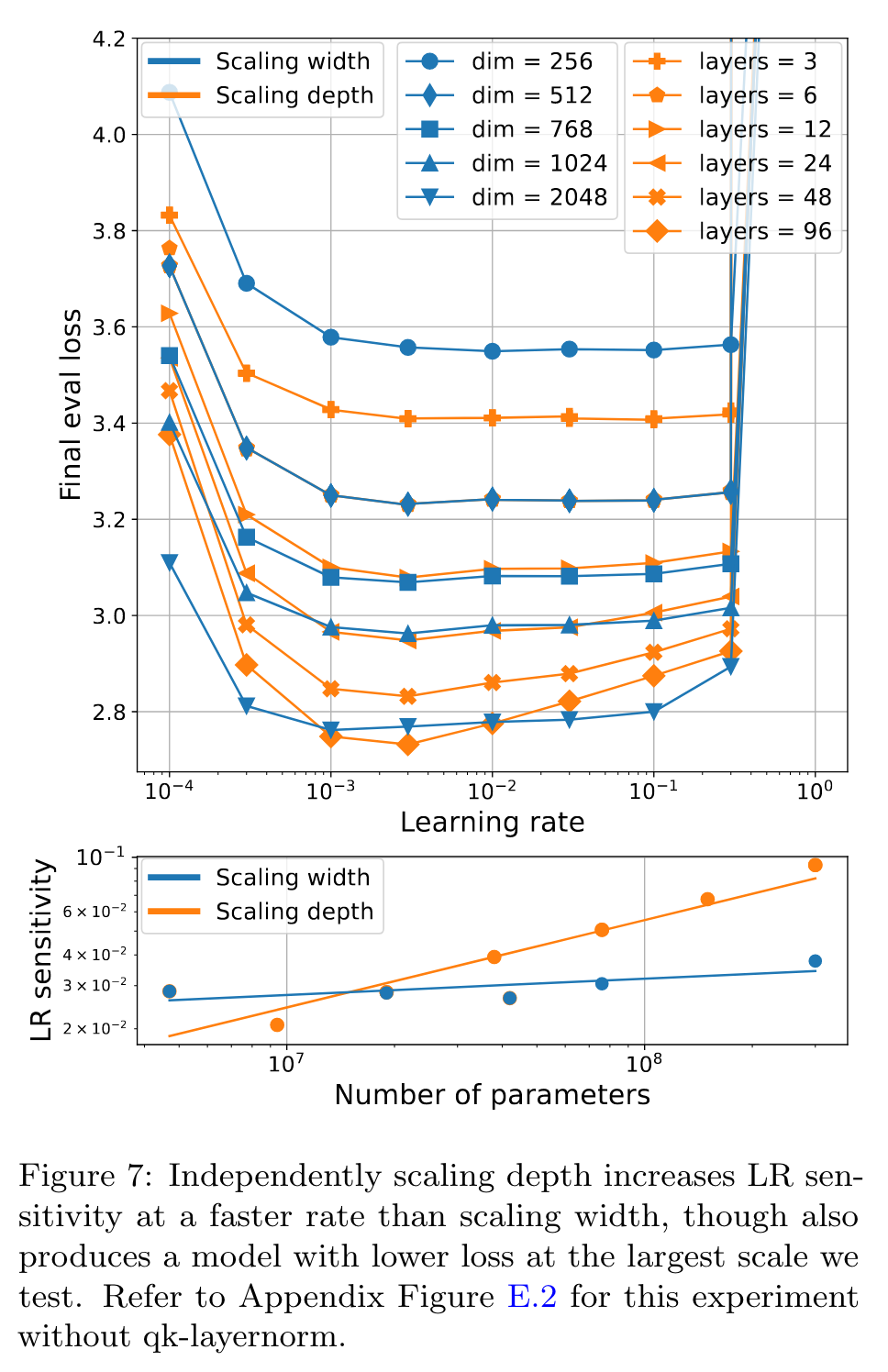
Our results, illustrated by Figure 7, indicate that scaling depth increases LR sensitivity at a faster rate than scaling width. However, at the largest scale we test, independently scaling depth produces a model with lower validation loss. (p. 6)
μParam
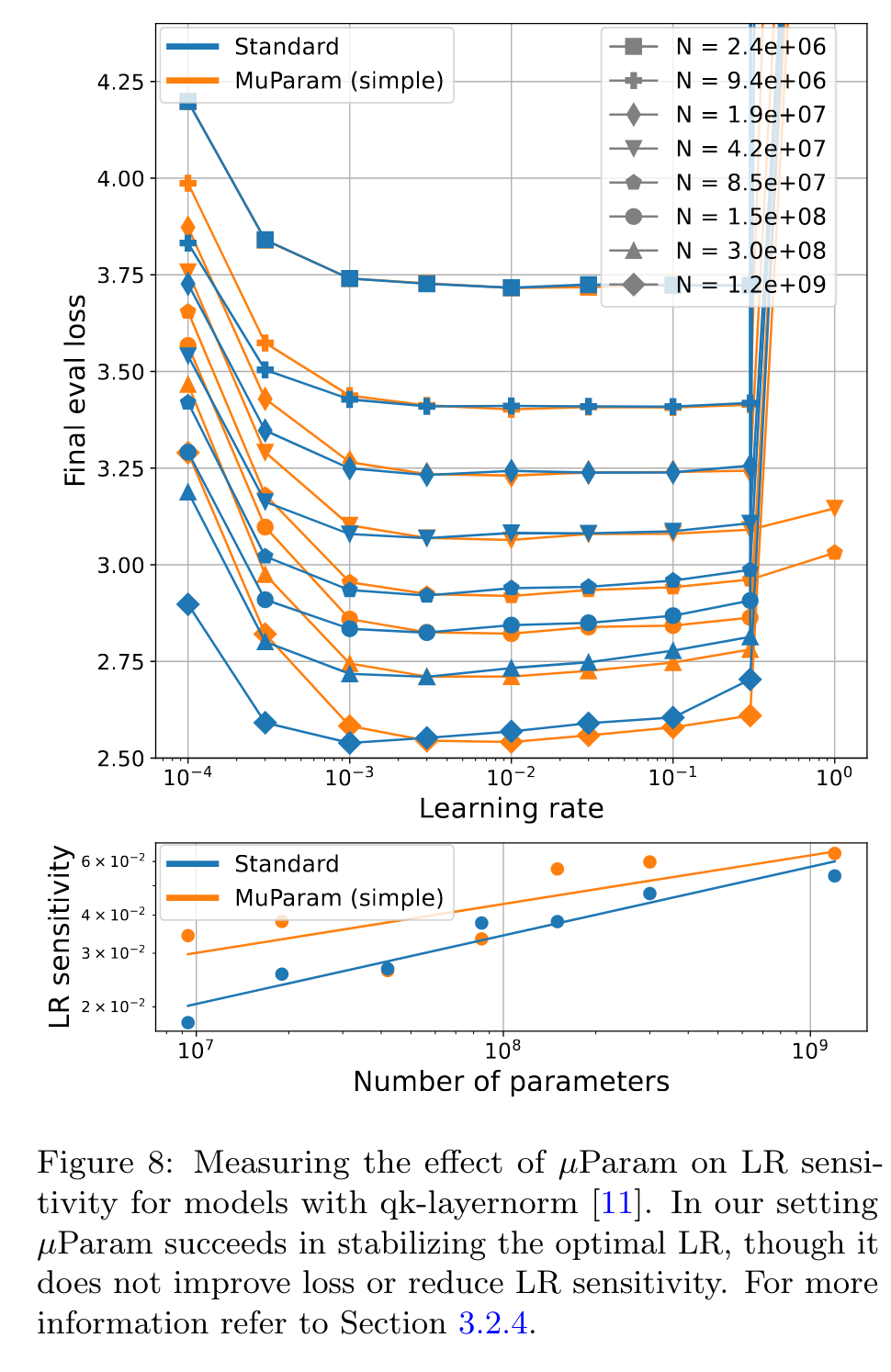
Yang and Hu [48] introduced the µParam method for parameterizing a neural network. As a product, the optimal LR remains consistent when scaling model width [49]. (p. 7)
µParam does succeed in stabilizing the optimal LR at the scale we test. However, µParam does not improve loss or reduce LR sensitivity in our experiments. Our results indicate that µParam does not alleviate the need for this intervention at high learning rates. (p. 7)
Additional interventions
- Changing the number of training steps from 1e5 to 5e4 or 2e5 does not meaningfully change LR sensitivity (Appendix Figure E.7).
- We try applying qk-layernorm across the whole model dimension instead of individually per-head with shared paramters. As illustrated in Appendix Figure E.8, the latter performs better. We use per-head qk-layernorm as the default in all other experiments.
- Increasing the batch size from 256 to 512 or 1024 does not meaningfully change LR sensitivity (Appendix Figure E.9, each batch element contains 512 tokens). When increasing batch size we decrease the number of training steps so that the amount of data seen is constant. We believe a similar effect would be observed if instead we held the number of steps constant because changing the number of steps has no impact on LR sensitivity at batch size 256 (Appendix Figure E.7).
- The effect of changing the weight decay from 1e-4 is illustrated in Figure E.10. Increasing decay appears to slightly shift the optimal LR right.
- We find that the logit growth instability is not due to the softmax in the self-attention layer, as it still occurs with a pointwise variant of attention (Appendix Figure E.11). (p. 8)
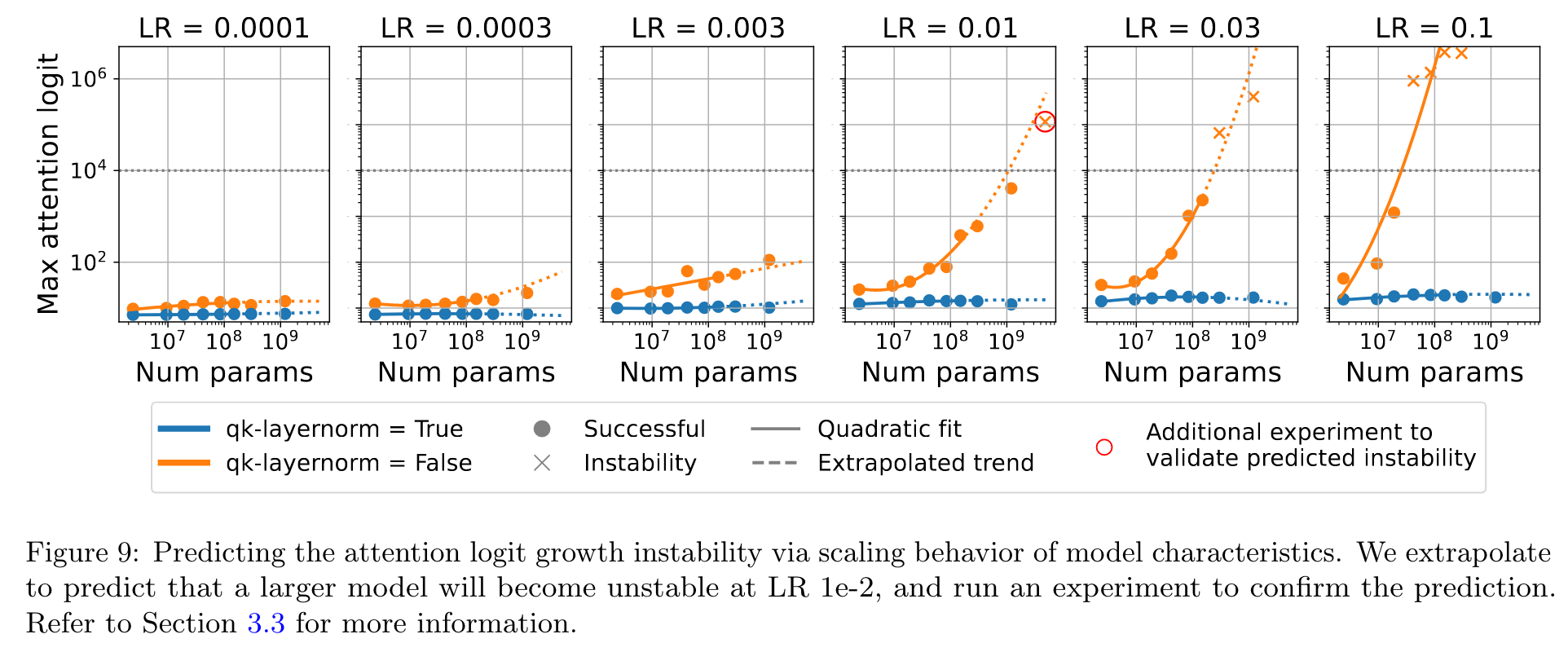
Predicting attention logit growth instability from scaling behavior of model characteristics
We first noticed that all points with attention logits above 1e4 diverged. Moreover, the quadratic fit predicted that for LR 1e-2 the next model scale would also cross that value. Based on this prediction, we trained a new 4.8B parameter model at LR 1e-2. This model diverged as predicted. Not only do we predict the divergence, but our fit closely extrapolates to predict the value of the max attention logit. (p. 8)
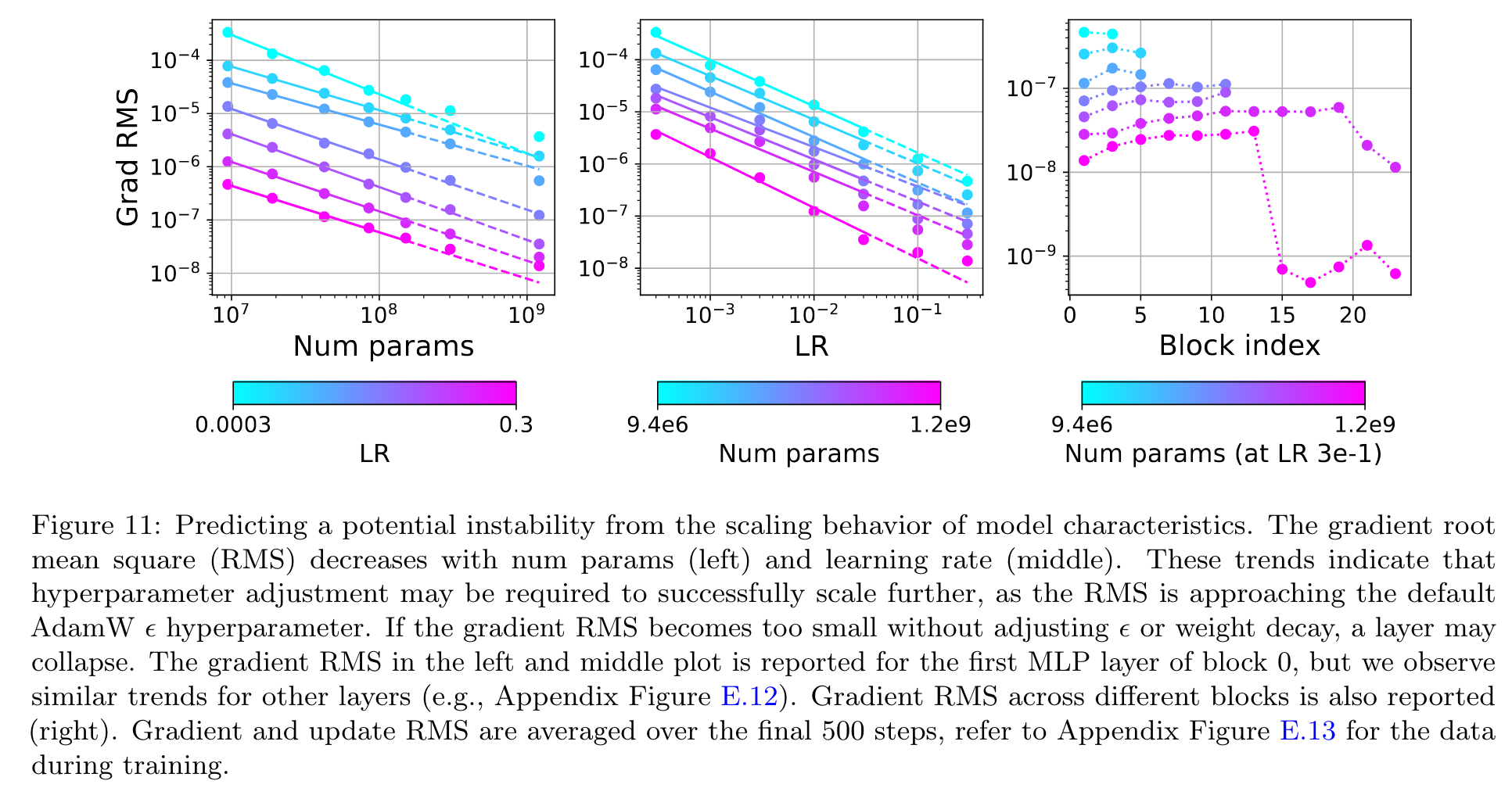
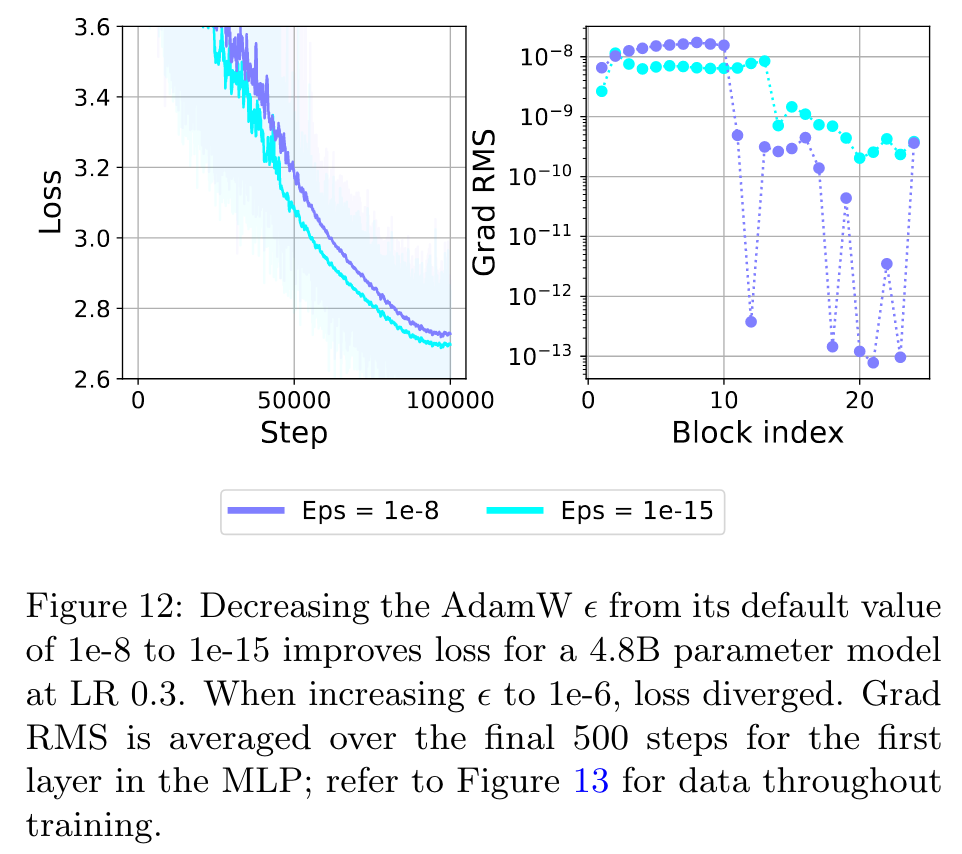
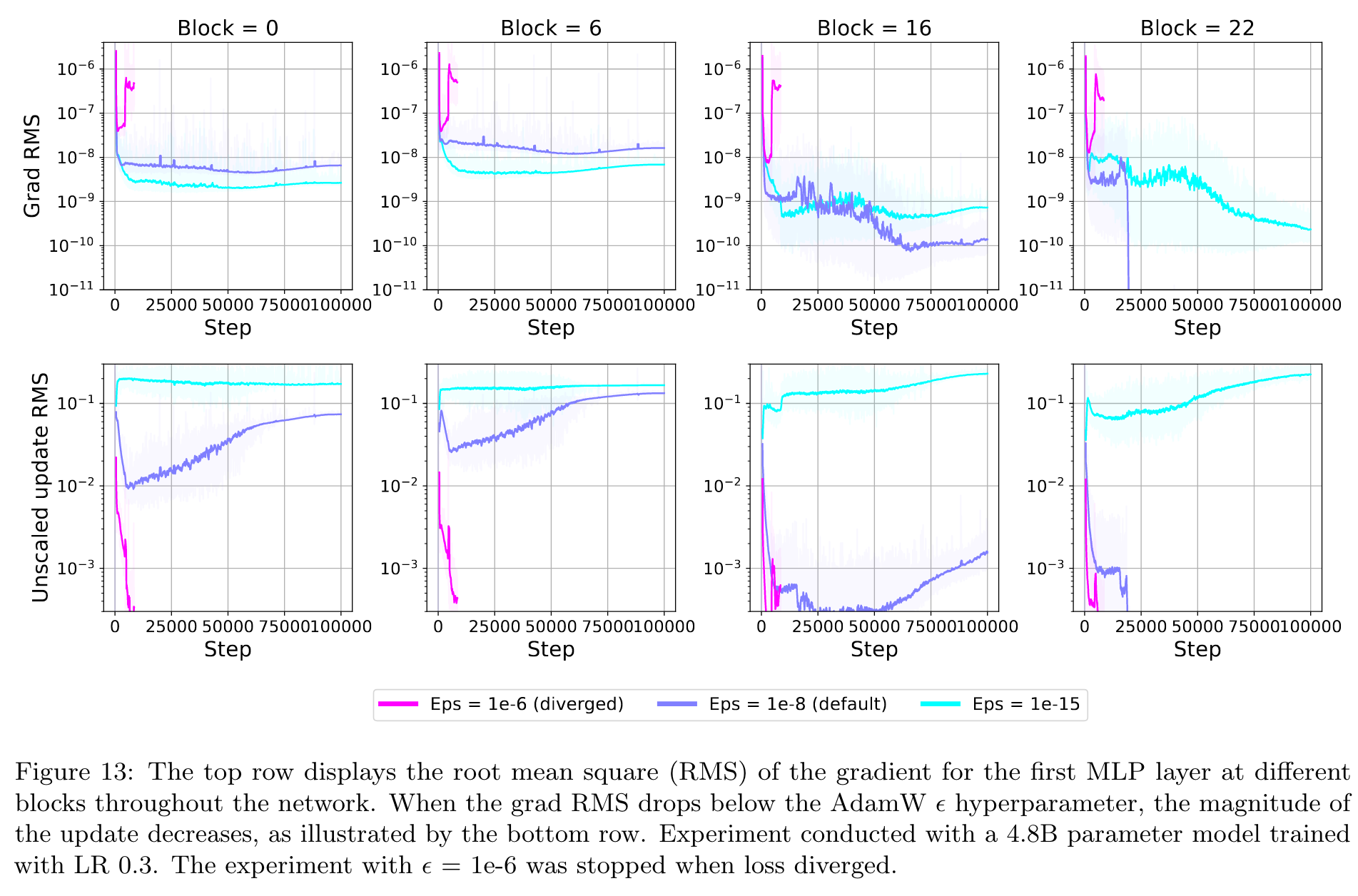
An obvious mitigation for this issue is to simply lower the AdamW ϵ hyperparameter from its default of 1e8 (p. 9)