Aligning Text-to-Image Diffusion Models with Reward Backpropagation
[reward reinforcement diffusion deep-learning bad align-prop text2image This is my reading note for Aligning Text-to-Image Diffusion Models with Reward Backpropagation. This paper proposes a method how to train diffusion model for a given reward function in a memory efficient way, especially it utilities Lora and checkpoints . To avoid model collapse, it also proposes to randomly truncate number of steps.

Introduction
Due to their unsupervised training, controlling their behavior in downstream tasks, such as maximizing human-perceived image quality, image-text alignment, or ethical image generation, is difficult. Recent works fine- tune diffusion models to downstream reward functions using vanilla reinforcement learning, notorious for the high variance of the gradient estimators. In this paper, we propose AlignProp, a method that aligns diffusion models to downstream re- ward functions using end-to-end backpropagation of the reward gradient through the denoising process. While naive implementation of such backpropagation would require prohibitive memory resources for storing the partial derivatives of modern text-to-image models, AlignProp finetunes low-rank adapter weight modules and uses gradient checkpointing, to render its memory usage viable. (p. 1)
This occurs because the models tend to adopt the noise, biases, and peculiarities inherent in the training data. In this paper, we consider the problem of training diffusion models to optimize downstream objectives directly, as opposed to matching a data distribution. (p. 2)
The most straightforward approach to aligning pre-trained models to downstream objectives is supervised fine-tuning on a small-scale human-curated dataset of high-quality model responses (p. 2)
On the other hand, it is much easier to ask humans for relative feedback by showing two or more samples. Hence, as a result, the common practice is to train a reward model by explicitly collecting data of human preferences by asking a human subject to rank a number of examples as per the desired metric. However, in the case of diffusion models, this leads to a unique challenge: given such a reward function, how does one update the weights of the diffusion model? (p. 2)
Even though the learned reward function is differentiable, it is non-trivial to update the diffusion model through the long chain of diffusion sampling as it would require prohibitive memory resources to store the partial derivatives of all neural layers and denoising steps. This can easily be on the order of several terabytes of GPU memory Wallace et al. (2023) for the scale of modern text-to-image diffusion models. As a result, the typical alternative is to use reinforcement learning and directly update the diffusion weights via REINFORCE. This is the most common approach today to align diffusion models with a reward function Black et al. (2023); Lee et al. (2023); Ziegler et al. (2020); Stiennon et al. (2020). However, RL methods are notorious for high variance gradients and hence often result in poor sample efficiency. (p. 2)
This policy effectively maps conditioning input prompts and sampled noise to output images, and fine-tunes the weights of the denoising model using end-to-end backpropagation through differentiable reward functions applied to the output-generated image. (p. 2)
We fine-tune low-rank adapter weights Hu et al. (2021), added to the original denoising U-Net, instead of the original weights, and we use gradient checkpointing Gruslys et al. (2016); Chen et al. (2016) to compute partial derivatives on demand, as opposed to storing them all at once. In this way, AlignProp incurs reasonable memory cost while only doubling the processing cost per training step, which gets compensated due to the fact that direct backdrop needs less number of steps to optimize. However, end-to-end backdrop quickly tends to over-optimize the model to excessively maximize the reward model leading to collapse. We address the over-optimization Gao et al. (2022) with randomized truncated backpropagation Tallec & Ollivier (2017), i.e., randomly sampling the denoising step up to which we back-propagate the reward. (p. 2)
We show adapted layers in early denoising steps align the semantic content while adapted layers in later denoising steps adapt the high frequency details to the downstream objective. (p. 2)
ALIGNPROP

We introduce a method that transforms denoising inference within text-to-image diffusion models into a differentiable recurrent policy, which adeptly correlates conditioning input prompts and sampled noise to produce output images. This approach facilitates fine-tuning of the denoising model’s weights through end-to-end backpropagation, guided by differentiable reward functions applied to the generated output image. (p. 4)
| The proposed model casts conditional image denoising as a single step MDP with states S = {(x_T , c), x_T ∼ N (0, 1)}, actions are the generated image samples, and the whole DDIM denoising chain of Eq. 1 corresponds to a differentiable policy that maps states to image samples: A = {x0 : x_0 ∼ π_θ(· | x_T , c), x_T ∼ N (0, 1) }. The reward function is a differentiable function of parameters ϕ that depends only on generated images R_ϕ(x+0), x+0 ∈ A. Given a dataset of prompts input P, our loss function reads: (p. 4) |
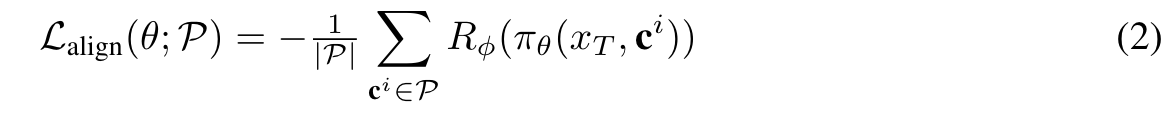
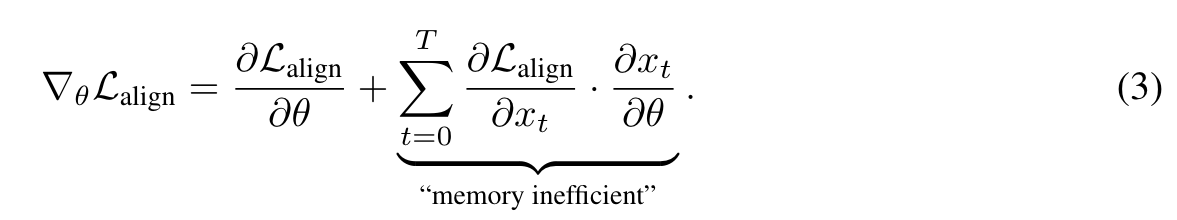
REDUCING MEMORY OVERHEAD
For instance, training StableDiffusion Rombach et al. (2022) using a batch size of 1 takes about 20GBs of GPU RAM, therefore training our policy πθ comprised of T chained denoising models with end-to-end backpropagation would require about 1TB of GPU RAM, which is infeasible. We use two design choice to enable full backpropagation through the denoising chain: 1. Finetuning low-rank adapter (LoRA) modules Hu et al. (2021) in place of the original diffusion weights, and 2. Gradient checkpointing for computing partial derivatives on demand Gruslys et al. (2016); Chen et al. (2016). (p. 5)
Finetuning LoRA weights
Effectively, this means we finetune 800K parameters instead of 800M, which reduces our GPU RAM usage by 2X to about 500GBs. (p. 5)
Gradient Checkpointing
Gradient checkpointing is a well known technique used to reduce the memory footprint of training neural networks Gruslys et al. (2016); Chen et al. (2016). Instead of storing all intermediate activations in memory for backpropagation, we only store a subset and recompute the rest on-the-fly during the backward pass. This allows for training deeper networks with limited memory at the cost of increased computation time. We find that gradient checkpointing significantly reduces our memory usage from 512 GBs to 15GBs, thus making it feasible to do full backpropogation on a single GPU. (p. 5)
RANDOMIZED TRUNCATED BACKPROPAGATION

During our experimentation, we encountered a significant issue with full backpropagation through time (BPTT) - it led to mode collapse within just two training epochs. Irrespective of the input conditioning prompt, we observed that the model consistently generated the same image. To address this challenge, we explored truncated backpropagation through time (TBTT) as an alternative strategy. However, TBTT introduces a bias towards short-term dependencies, as it restricts the backpropagation to a fixed number of steps, denoted as K (a hyperparameter). This bias can affect gradient estimates and hinder the model’s ability to capture long-range dependencies effectively. (Tallec & Ollivier, 2017) demonstrated that the bias introduced by truncation in the backpropagation through time algorithm can be mitigated by randomizing the truncation lengths, i.e., varying the number of time-steps for which backpropagation occurs.
Our human evaluation experiments, detailed in Section 5, provided valuable insights. It was observed that setting K ∼ Uniform(0, 50) yielded the most promising results in terms of aligned image generation. (p. 5)
EXPERIMENTS
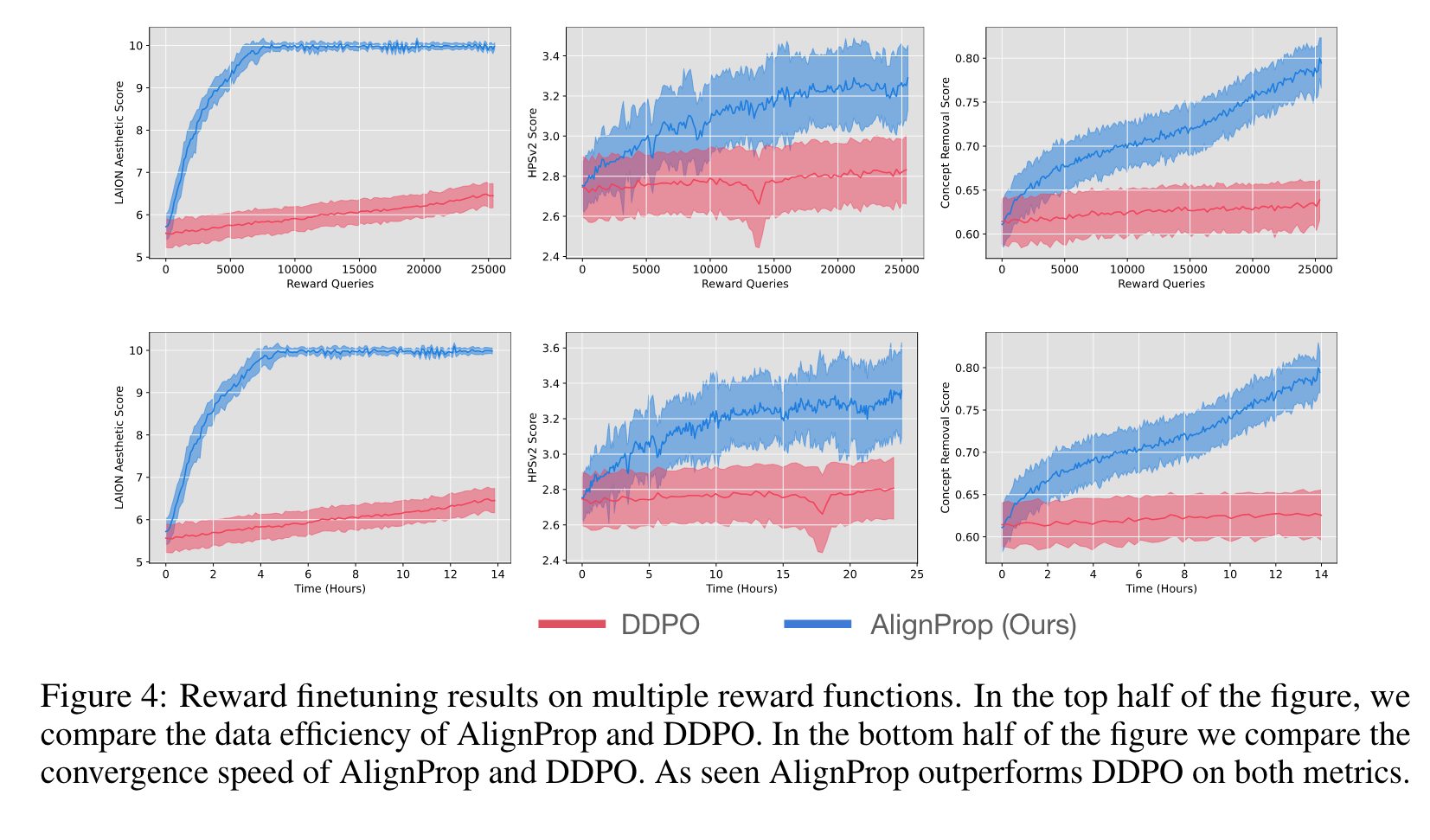
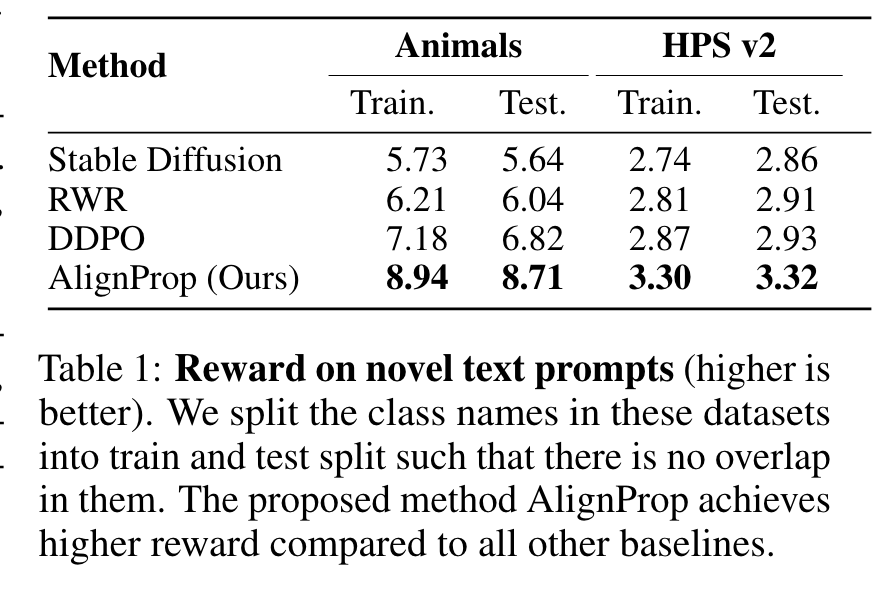
AlignProp achieves a score of 0.28 in just 48 minutes, whereas DDPO requires approximately 23 hours, highlighting a substantial 25-fold ac- celeration in convergence speed. (p. 7)

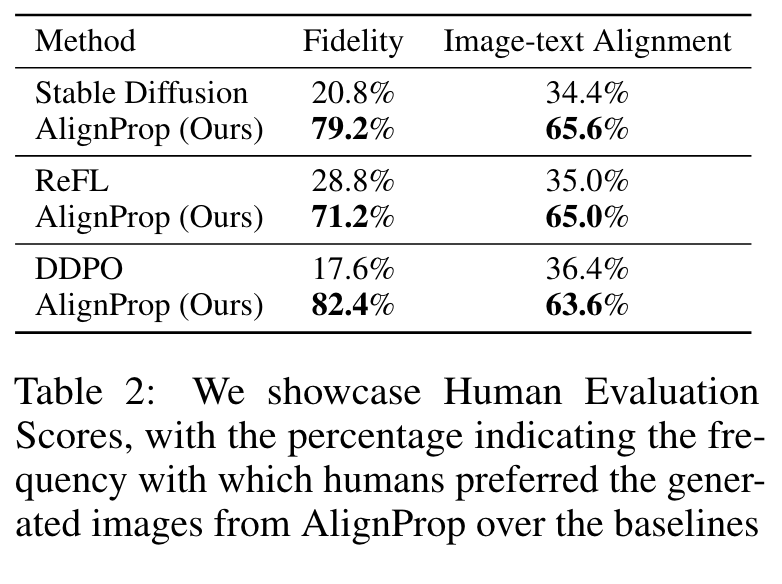

Ablations