Diffusion Model
[diffusion gan autoregressor deep-learning denoising This is my 1st reading note of on recent progress of difussion model. It is based on Diffusion Models: A Comprehensive Survey of Methods and Applications. Diffusion probabilistic models were originally proposed as a latent variable generative model inspired by non- equilibrium thermodynamics. The essential idea of diffusion models is to systematically perturb the structure in a data distribution through a forward diffusion process, and then recover the structure by learning a reverse diffusion process, resulting in a highly flexible and tractable generative model.
However, original diffusion models still suffer from limitations, including:
- a slow sampling procedure, which usually requires thousands of evaluation steps to draw a sample
- Also, it struggles to achieve competitive log-likelihoods compared to likelihood-based models, such as autoregressive models.
- poor data generalization ability
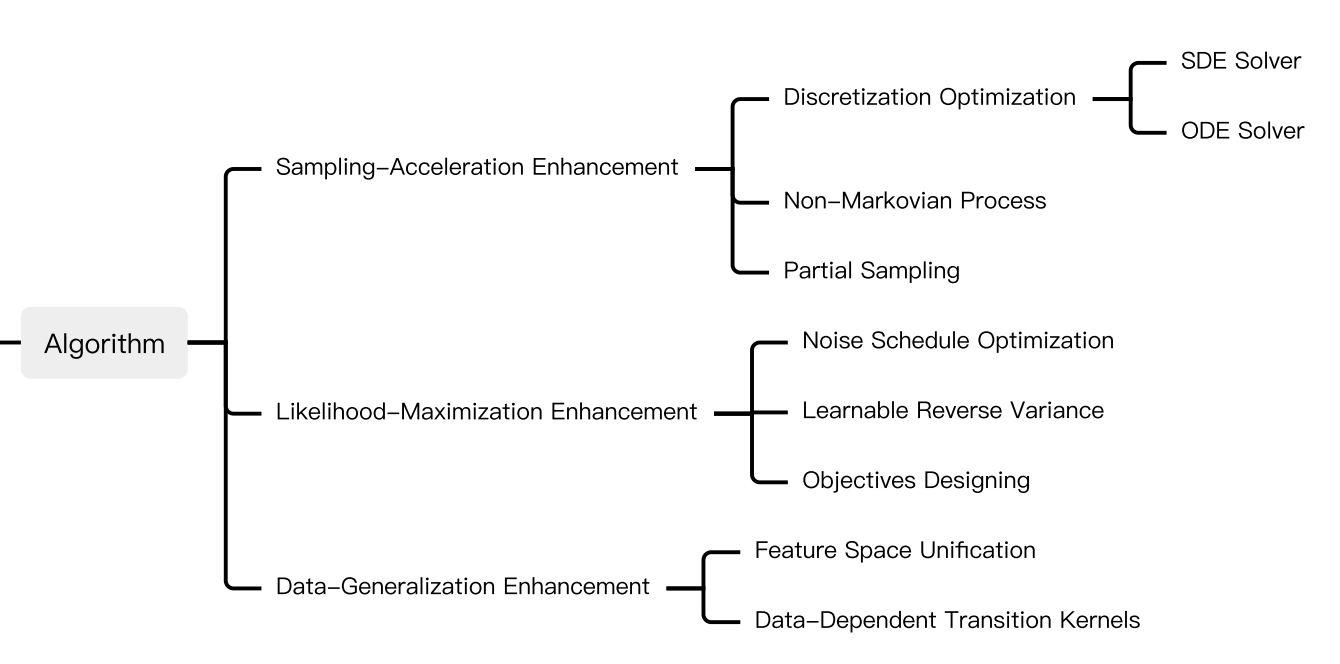
Many efforts are maded are made to address those limitations, which are roughly categorized as below:
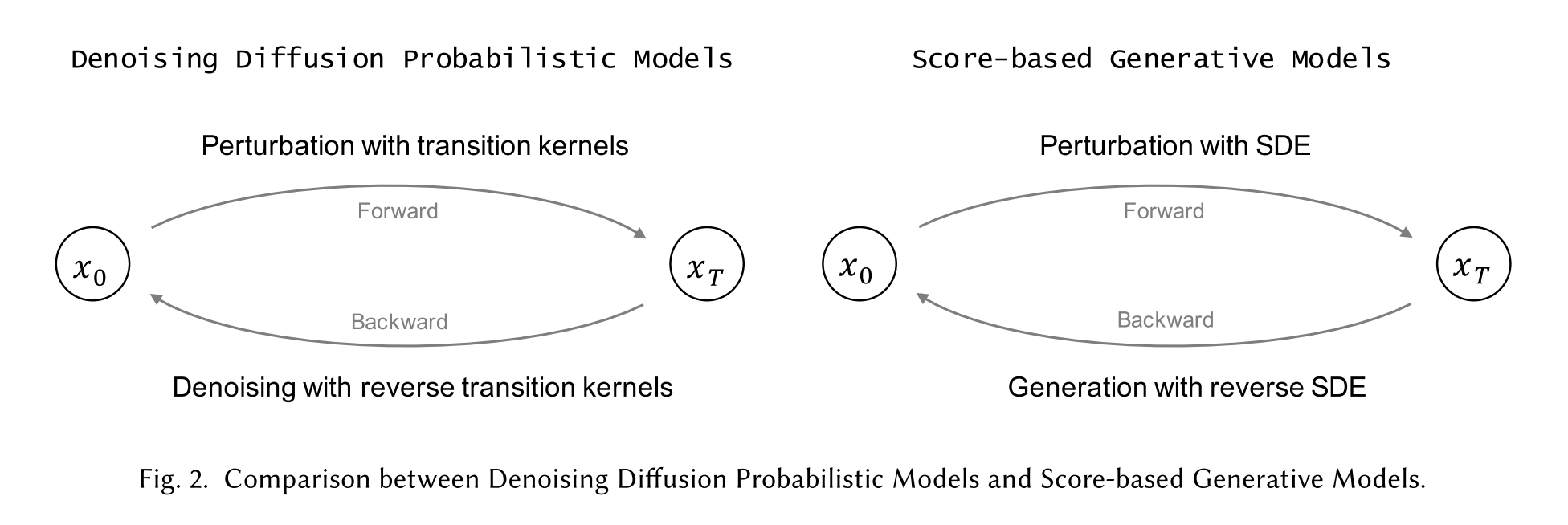
Denoising Diffusion Probabilistic Models
A denoising diffusion probabilistic model (DDPM) [78] consists of two parameterized Markov chains and uses varia- tional inference to generate samples matching the original data after a finite time. The forward chain perturbs the data distribution by gradually adding Gaussian noise with a pre-designed schedule until the data distribution converges to a given prior, i.e., standard Gaussian distribution. The reverse chain starts with the given prior and uses a parameterized Gaussian transition kernel, learning to gradually restore the undisturbed data structure.
Score-based Generative Models
Alternatively, one can view the aforementioned diffusion probabilistic model as a discretization of a score-based generative model. Score-based generative models construct a stochastic differential equation (SDE) to disturb a data distribution to a known prior distribution in a smooth fashion and a corresponding reverse-time SDE to transform the prior distribution back into the data distribution.
