DreamFusion Text-to-3D using 2D Diffusion
[dream-field 3d diffusion nerf score-distillation-sampling deep-learning sds dream-fusion This is my reading note on DreamFusion: Text-to-3D using 2D Diffusion. This paper proposes a method (score distillation sampling or SDS) to distill a pre-trained text to image diffusion model to a 3D model. The 3D model, which is based on NERF, is trained per text prompt.
Introduction
Recent breakthroughs in text-to-image synthesis have been driven by diffusion models trained on billions of image-text pairs. Adapting this approach to 3D synthesis would require large-scale datasets of labeled 3D data and efficient architectures for denoising 3D data, neither of which currently exist. In this work, we circumvent these limitations by using a pretrained 2D text-to-image diffusion model to perform text-to-3D synthesis. We introduce a loss based on probability density distillation that enables the use of a 2D diffusion model as a prior for optimization of a parametric image generator. Using this loss in a DeepDream-like procedure, we optimize a randomly-initialized 3D model (a Neural Radiance Field, or NeRF) via gradient descent such that its 2D renderings from random angles achieve a low loss. The resulting 3D model of the given text can be viewed from any angle, relit by arbitrary illumination, or composited into any 3D environment. Our approach requires no 3D training data and no modifications to the image diffusion model, demonstrating the effectiveness of pretrained image diffusion models as priors.
Recent breakthroughs in text-to-image synthesis have been driven by diffusion models trained on billions of image-text pairs. Adapting this approach to 3D synthesis would require large-scale datasets of labeled 3D data and efficient architectures for denoising 3D data, neither of which currently exist. In this work, we circumvent these limitations by using a pretrained 2D text-to-image diffusion model to perform text-to-3D synthesis. We introduce a loss based on probability density distillation that enables the use of a 2D diffusion model as a prior for optimization of a parametric image generator. Using this loss in a DeepDream-like procedure, we optimize a randomly-initialized 3D model (a Neural Radiance Field, or NeRF) via gradient descent such that its 2D renderings from random angles achieve a low loss. The resulting 3D model of the given text can be viewed from any angle, relit by arbitrary illumination, or composited into any 3D environment. Our approach requires no 3D training data and no modifications to the image diffusion model, demonstrating the effectiveness of pretrained image diffusion models as priors. See dreamfusion3d.github.io for a more immersive view into our 3D results. (p. 1)
3D generative models can be trained on explicit representations of structure like voxels (Wu et al., 2016; Chen et al., 2018) and point clouds (Yang et al., 2019; Cai et al., 2020; Zhou et al., 2021), but the 3D data needed is relatively scarce compared to plentiful 2D images. Our approach learns 3D structure using only a 2D diffusion model trained on images, and sidesteps this issue. GANs can learn controllable 3D generators from photographs of a single object category, by placing an adversarial loss on 2D image renderings of the output 3D object or scene (Henzler et al., 2019; Nguyen-Phuoc et al., 2019; Or-El et al., 2022). Though these approaches have yielded promising results on specific object categories such as faces, they have not yet been demonstrated to support arbitrary text. (p. 1)

Many 3D generative approaches have found success in incorporating NeRF-like models as a building block within a larger generative system (Schwarz et al., 2020; Chan et al., 2021b;a; Gu et al., 2021; Liu et al., 2022). One such approach is Dream Fields (Jain et al., 2022), which uses frozen image-text joint embedding models from CLIP and an optimization-based approach to train NeRFs. This work showed that pretrained 2D image-text models may be used for 3D synthesis, though 3D objects produced by this approach tend to lack realism and accuracy. CLIP has been used to guide other approaches based on voxel grids and meshes (Sanghi et al., 2022; Jetchev, 2021; Wang et al., 2022). (p. 3)
We adopt a similar approach to Dream Fields, but replace CLIP with a loss derived from distillation of a 2D diffusion model. Our loss is based on probabilty density distillation, minimizing the KL divergence between a family of Gaussian distribution with shared means based on the forward process of diffusion and the score functions learned by the pretrained diffusion model. The resulting Score Distillation Sampling (SDS) method enables sampling via optimization in differentiable image parameterizations. By combining SDS with a NeRF variant tailored to this 3D generation task, DreamFusion generates high-fidelity coherent 3D objects and scenes for a diverse set of user-provided text prompts. (p. 3)
SCORE DISTILLATION SAMPLING
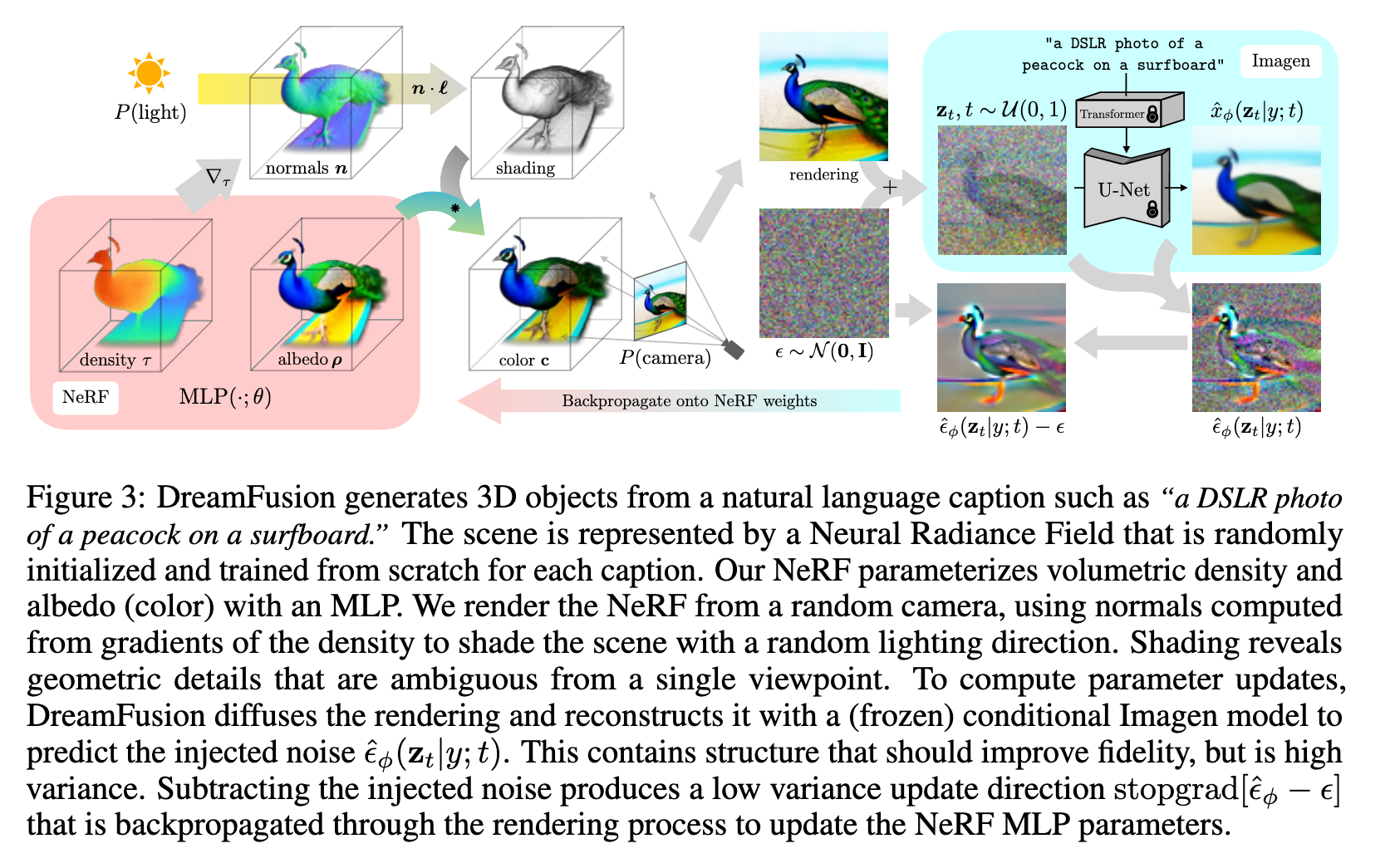
Though conditional diffusion sampling enables quite a bit of flexibility (e.g. inpainting), diffusion models trained on pixels have traditionally been used to sample only pixels. We are not interested in samplingpixels; we instead want to create 3D models that look like good images when rendered from random angles. Such models can be specified as a differentiable image parameterization (DIP,Mordvintsev et al., 2018), where a differentiable generator g transforms parameters θ to create an image x = g(θ). DIPs allow us to express constraints, optimize in more compact spaces (e.g.arbitrary resolution coordinate-based MLPs), or leverage more powerful optimization algorithms fortraversing pixel space. For 3D, we let θ be parameters of a 3D volume and g a volumetric renderer.To learn these parameters, we require a loss function that can be applied to diffusion models. (p. 4)
Our approach leverages the structure of diffusion models to enable tractable sampling via optimization— a loss function that, when minimized, yields a sample. We optimize over parameters θ such that x = g(θ) looks like a sample from the frozen diffusion model. (p. 4)
Minimizing the diffusion training loss with respect to a generated datapoint x = g(θ) gives $\theta^∗ = \mbox{argmin}\theta L{Diff}(\phi, x = g(\theta))$. In practice, we found that this loss function did not produce realistic samples even when using an identity DIP where x = θ. Concurrent work from Graikos et al.(2022) shows that this method can be made to work with carefully chosen timestep schedules, but we found this objective brittle and its timestep schedules challenging to tune. (p. 4)
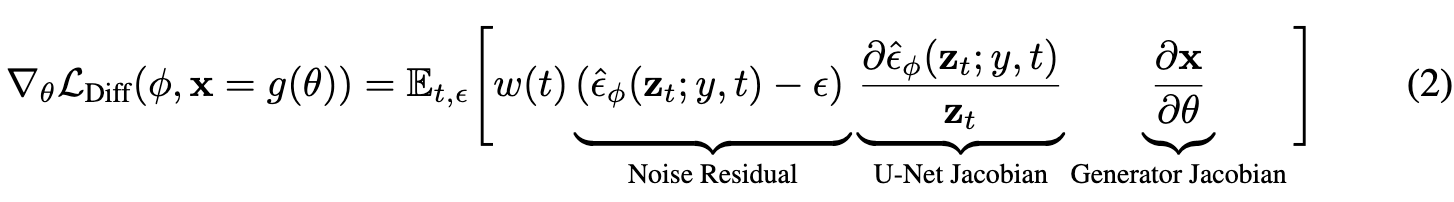
In practice, the U-Net Jacobian term is expensive to compute (requires back propagating through the diffusion model U-Net), and poorly conditioned for small noise levels as it is trained to approximate the scaled Hessian of the marginal density. We found that omitting the U-Net Jacobian term leads to an effective gradient for optimizing DIPs with diffusion models: (p. 4)
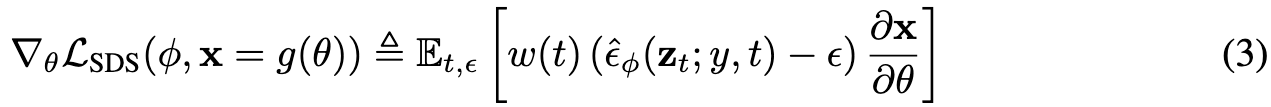
Intuitively, this loss perturbs x with a random amount of noise corresponding to the timestep t, and estimates an update direction that follows the score function of the diffusion model to move to a higher density region. While this gradient for learning DIPs with diffusion models may appear ad hoc, in Appendix A.4 we show that it is the gradient of a weighted probability density distillation loss (van den Oord et al., 2018) using the learned score functions from the diffusion model: (p. 4)
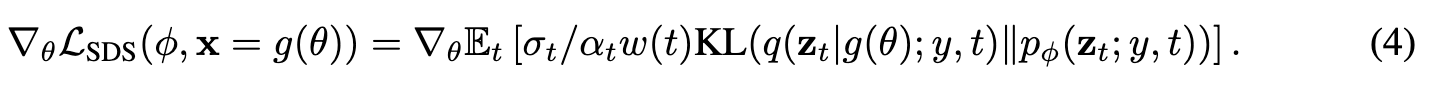
| We name our sampling approach Score Distillation Sampling (SDS) as it is related to distillation, but uses score functions instead of densities. We refer to it as a sampler because the noise in the variational family q(zt | . . .) disappears as t → 0 and the mean parameter of the variational distribution g(θ)becomes the sample of interest. (p. 5) |
Since the diffusion model directly predicts the update direction, we donot need to backpropagate through the diffusion model; the model simply acts like an efficient, frozen critic that predicts image-space edits. (p. 5)
Empirically, we found that setting the guidance weight ω to a large value for classifier-free guidance improves quality (Appendix Table 9). SDS produces detail comparable to ancestral sampling, but enables new transfer learning applications because it operates in parameter space. (p. 5)
Proposed Method
For the diffusion model, we use the Imagen model from Saharia et al. (2022), which has been trained to synthesize images from text. We only use the 64 × 64 base model (not the super-resolution cascade for generating higher-resolution images), and use this pretrained model as-is with no modifications. To synthesize a scene from text, we initialize a NeRF-like model with random weights, then repeatedly render views of that NeRF from random camera positions and angles, using these renderings as the input to our score distillation loss function that wraps around Imagen. (p. 5)
NEURAL RENDERING OF A 3D MODEL
Our model is built upon mip-NeRF 360 (Barron et al., 2022), which is an improved version of NeRF that reduces aliasing. (p. 6). We shade the color based on opacity as well as the surface normal.
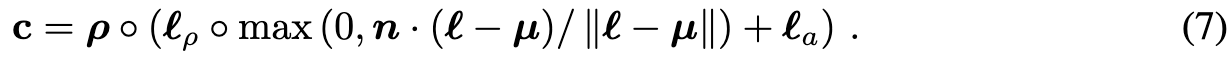
Scene Structure.
While our method can generate some complex scenes, we find that it is helpful toonly query the NeRF scene representation within a fixed bounding sphere, and use an environment map generated from a second MLP that takes positionally-encoded ray direction as input to compute a background color. We composite the rendered ray color on top of this background color using the accumulated alpha value. This prevents the NeRF model from filling up space with density very close to the camera while still allowing it to paint an appropriate color or backdrop behind the generated scene. For generating single objects instead of scenes, a reduced bounding sphere can be useful. (p. 6)
Geometry regularizers
We use the orientation loss proposed by Ref-NeRF (Verbin et al.,2022) to encourage normal vectors of the density field to face toward the camera when they are visible (so that the camera does not observe geometry that appears to face “backwards” when shaded).We place a stop-gradient on the rendering weights wi, which helps prevent unintended local minima where the generated object shrinks or disappears (p. 16). If orientation loss is too high, surfaces become oversmoothed. (p. 16)
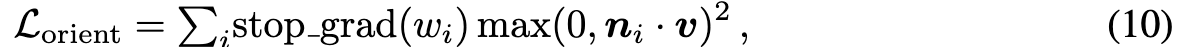
We also apply a small regularization to the accumulated alpha value (opacity) along each ray: Lopacity = √(∑i wi)2 + 0.01. This discourages optimization from unnecessarily filling in empty space, and improves foreground/background separation. (p. 16)
TEXT-TO-3D SYNTHESIS
For each text prompt, we train a randomly initialized NeRF from scratch. Each iteration of DreamFusion optimization performs the following: (1) randomly sample a camera and light, (2) render an image of the NeRF from that camera and shade with the light, (3) compute gradients of the SDS loss with respect to the NeRF parameters, (4) update the NeRF parameters using an optimizer. (p. 7)
- Random camera and light sampling. At each iteration, a camera position is randomly sampledin spherical coordinates, with elevation angle φcam ∈ [−10°, 90°], azimuth angle θcam ∈ [0°, 360°],and distance from the origin in [1, 1.5]. For reference, the scene bounding sphere described previously has radius 1.4. We also sample a “look-at” point around the origin and an “up” vector, and combine these with the camera position to create a camera pose matrix. We additionally sample a focal length multiplier λfocal ∈ U (0.7, 1.35) such that the focal length is λfocalw, where w = 64 is the image width in pixels. The point light position l is sampled from a distribution centered around the camera position. We found using a wide range of camera locations to be critical for synthesizing coherent 3D scenes, and a wide range of camera distances helps to improve the resolution of the learned scene. (p. 7)
- We randomly choose between the illuminated colorrender, a textureless render, and a rendering of the albedo without any shading. (p. 7)
- We therefore found it beneficial to append view-dependent text to the provided input text based on the location of the randomly sampled camera. (p. 7). For classifier-free guidance, we set ω = 100, finding that higher guidance weights give improved sample quality. This is much larger than image sampling methods, and is likely required due to the mode-seeking nature of our objective which results in oversmoothing at small guidance weights (see Appendix Table. 9). Given the rendered image and sampled timestep t, we sample noise and compute the gradient of the NeRF parameters according to Eqn. 3. (p. 7)

Experiment Result

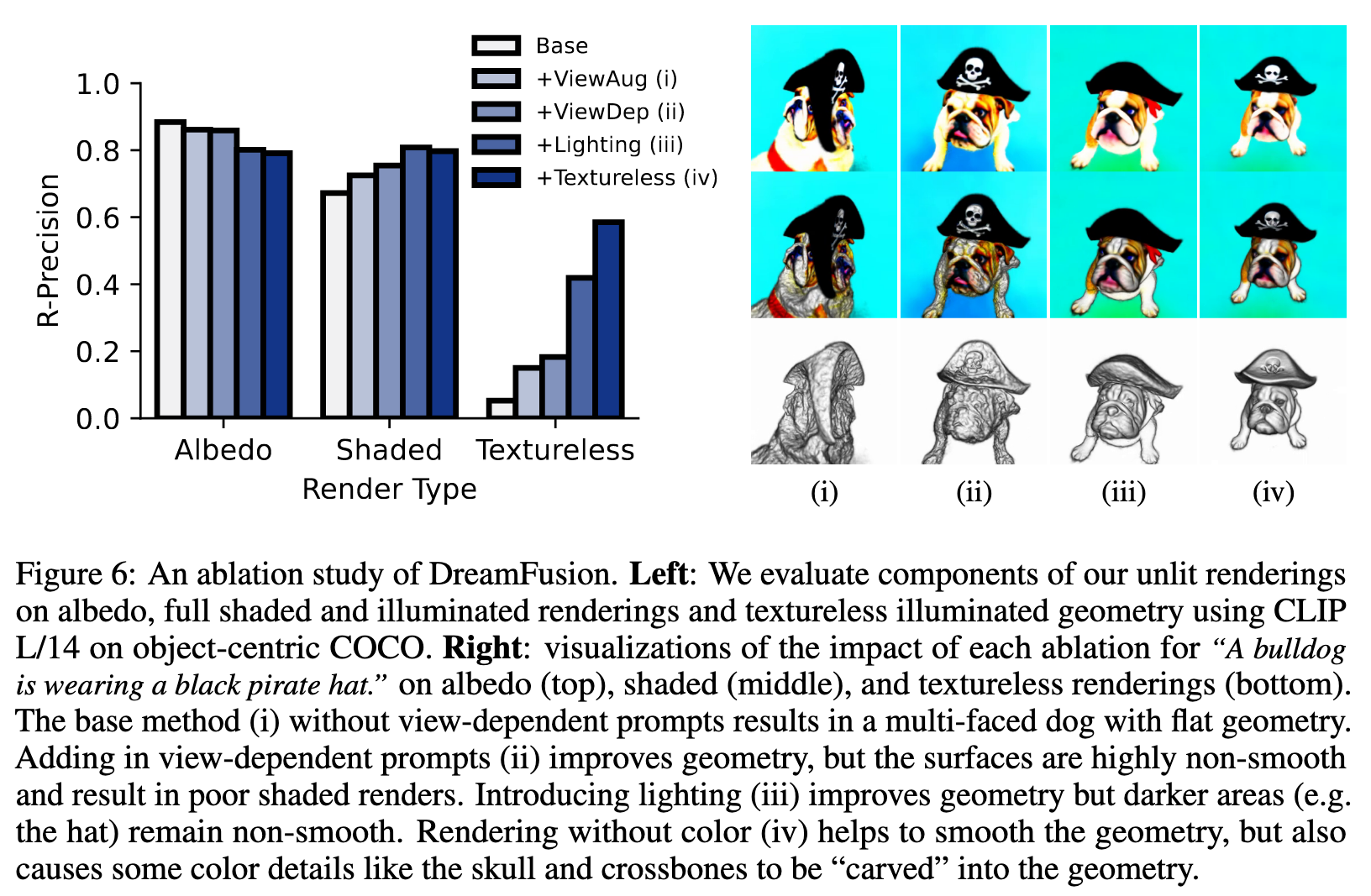
Limitations
Though DreamFusion produces compelling results and outperforms prior work on this task, it still has several limitations. SDS is not a perfect loss function when applied to image sampling, and often produces oversaturated and oversmoothed results relative to ancestral sampling. While dynamic thresholding (Saharia et al., 2022) partially ameliorates this issue when applying SDS to images, it did not resolve this issue in a NeRF context. Additionally, 2D image samples produced using SDS tend to lack diversity compared to ancestral sampling, and our 3D results exhibit few differences across random seeds. This may be fundamental to our use of reverse KL divergence, which has been previously noted to have mode-seeking properties in the context of variational inference and probability density distillation. (p. 9)
DreamFusion uses the 64 × 64 Imagen model, and as such our 3D synthesized models tend to lackfine details. Using a higher-resolution diffusion model and a bigger NeRF would presumably address this, but synthesis would become impractically slow. Hopefully improvements in the efficiency of diffusion and neural rendering will enable tractable 3D synthesis at high resolution in the future. (p. 9)
