InstaFlow One Step is Enough for High-Quality Diffusion-Based Text-to-Image Generation
[instantflow diffusion distill deep-learning rectified-flow progressive-distillation text2image ode This is my reading note on InstaFlow One Step is Enough for High-Quality Diffusion-Based Text-to-Image. This paper proposes a way to speed up diffusion based method, by achieving high fidelity with one step of diffusion. The key to this method is to use rectified how to straighten the probability flow from model to the final image. After that the model could be distilled to one step diffusion.
Introduction
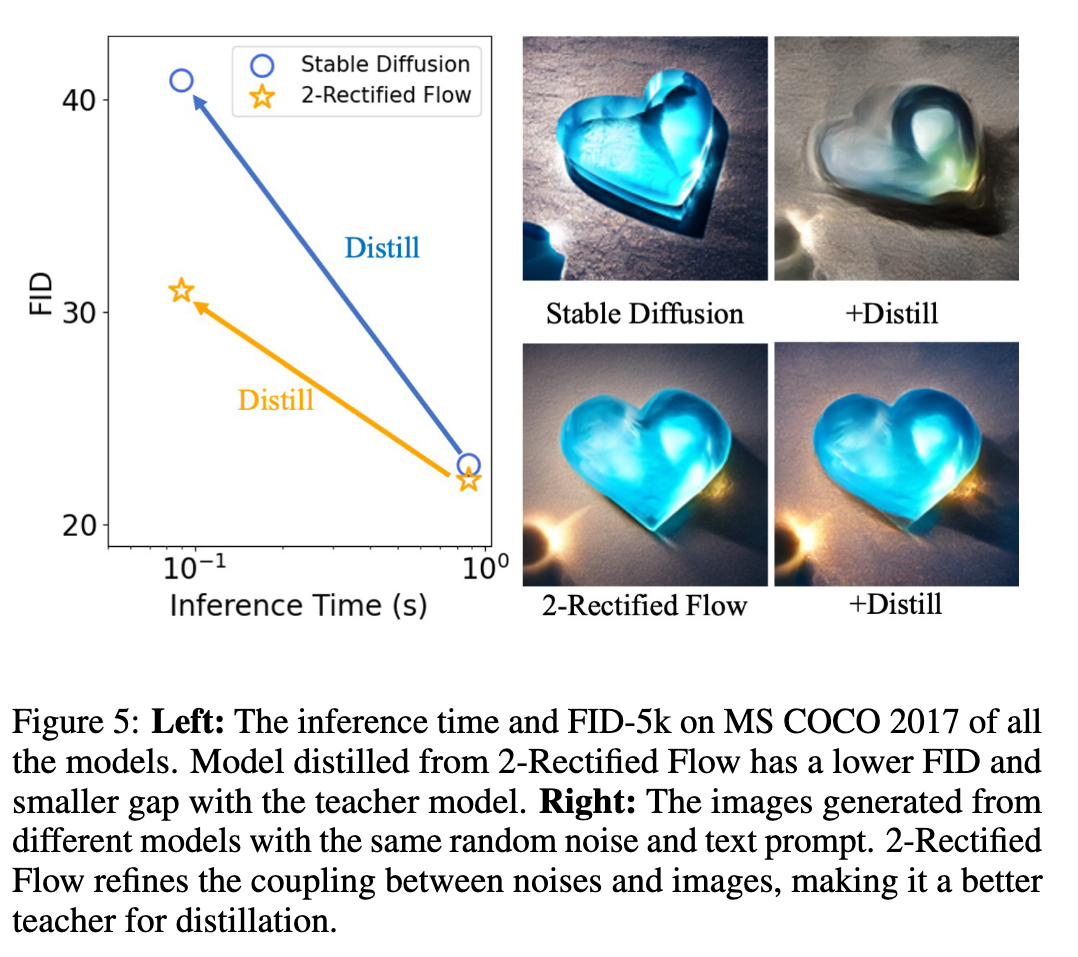
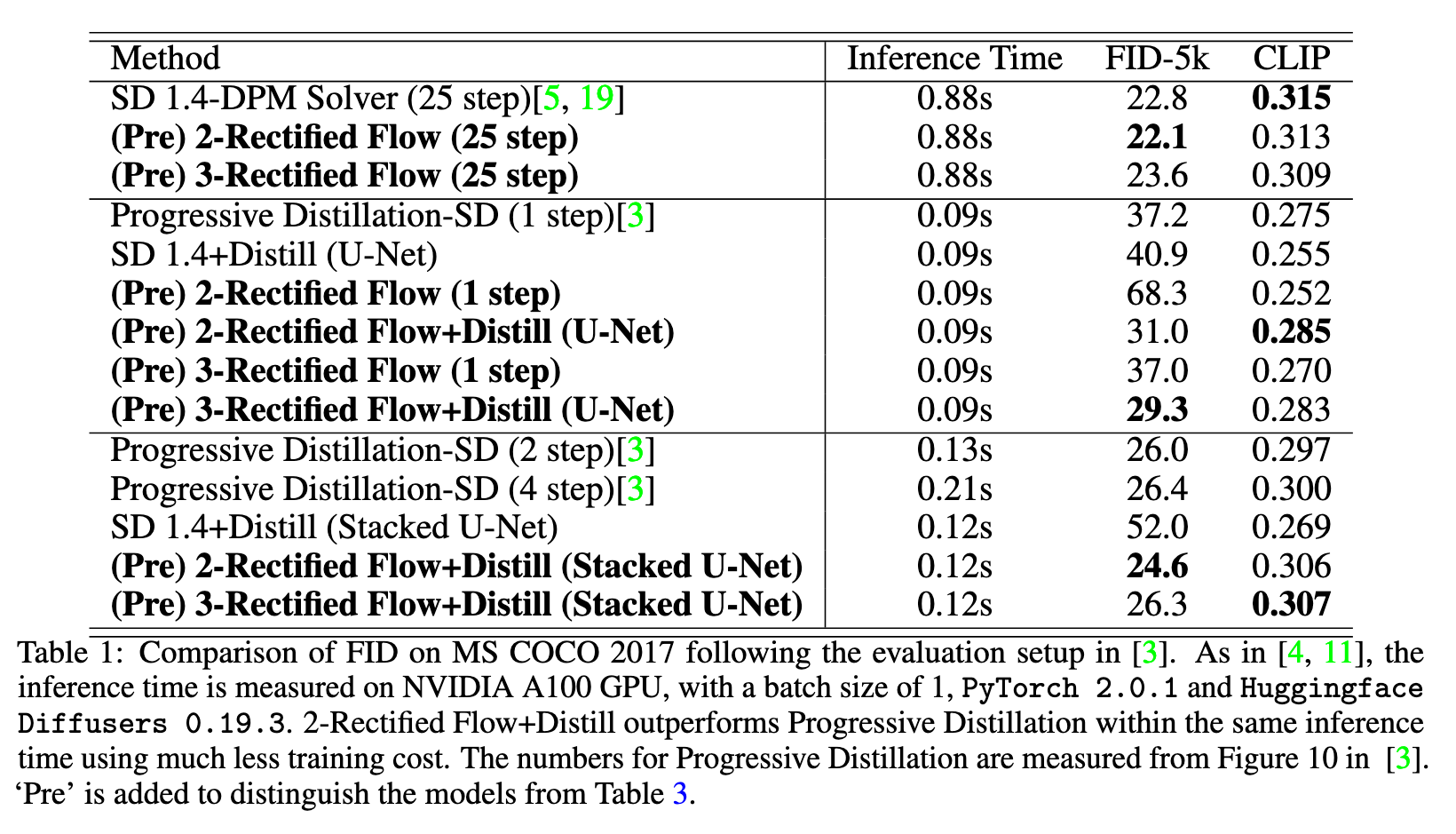
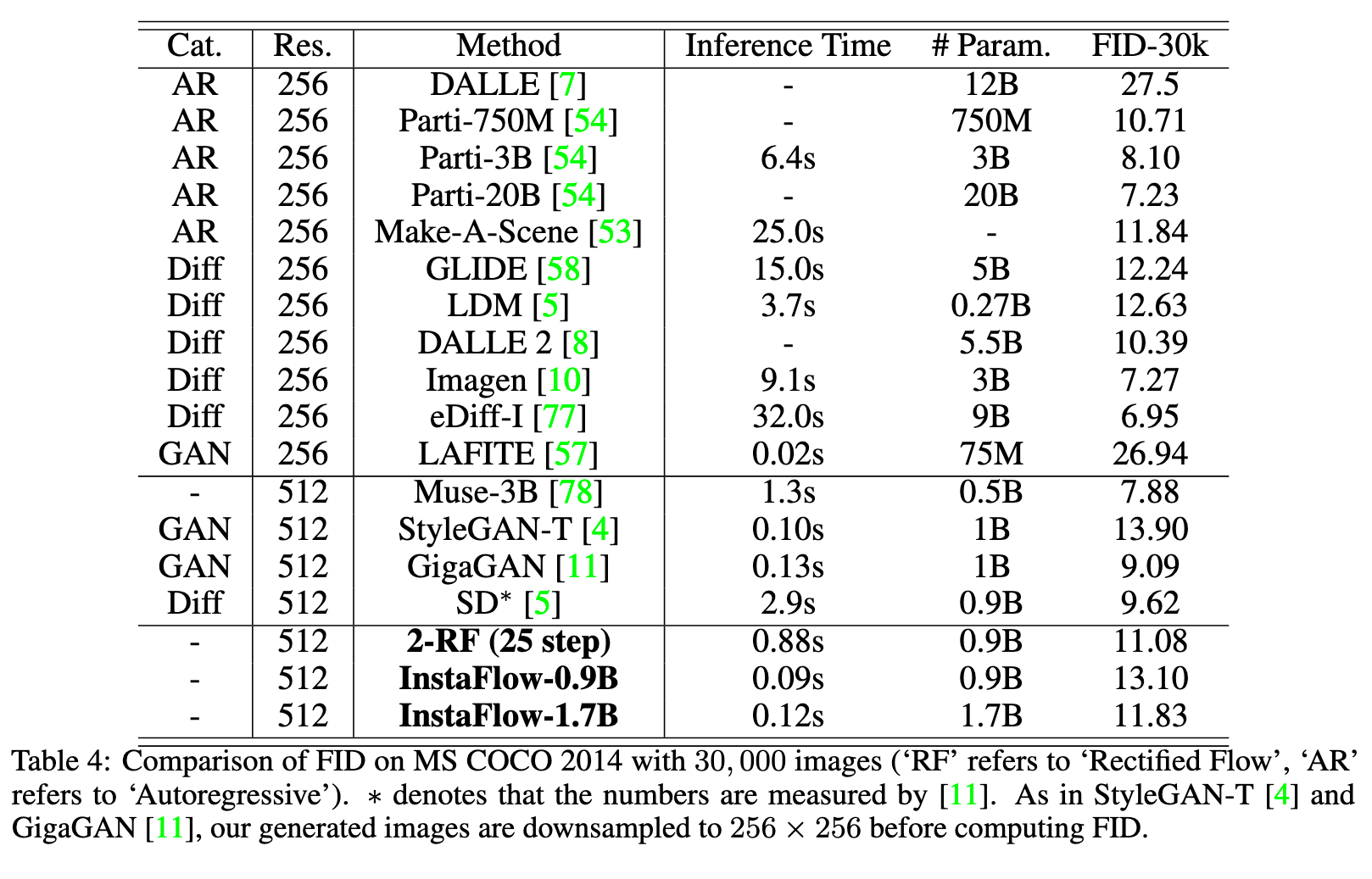
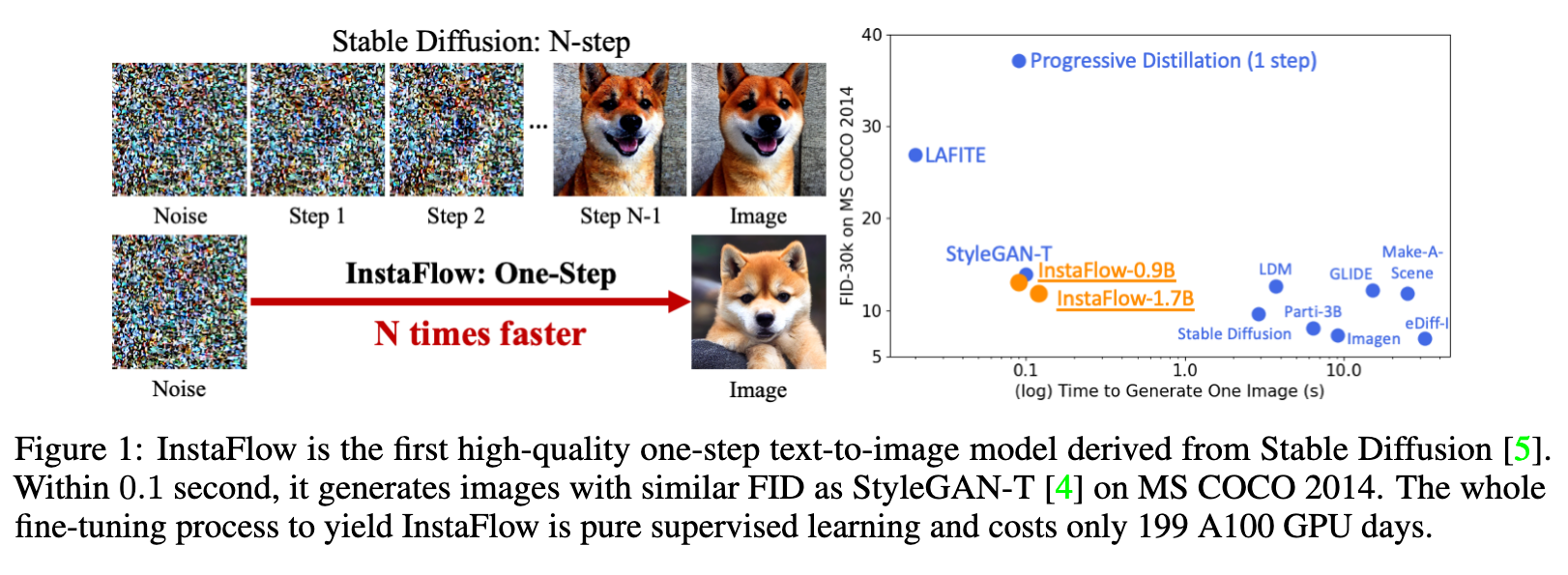
In this paper, we explore a recent method called Rectified Flow [1, 2], which, thus far, has only been applied to small datasets. The core of Rectified Flow lies in its reflow procedure, which straightens the trajectories of probability flows, refines the coupling between noises and images, and facilitates the distillation process with student models. We propose a novel text-conditioned pipeline to turn Stable Diffusion (SD) into an ultra-fast one-step model, in which we find reflow plays a critical role in improving the assignment between noise and images. Leveraging our new pipeline, we create, to the best of our knowledge, the first one-step diffusion-based text-to-image generator with SD-level image quality, achieving an FID (Fréchet Inception Distance) of 23.3 on MS COCO 2017-5k, surpassing the previous state-of-the-art technique, progressive distillation [3], by a significant margin (37.2 → 23.3 in FID) (p. 1)
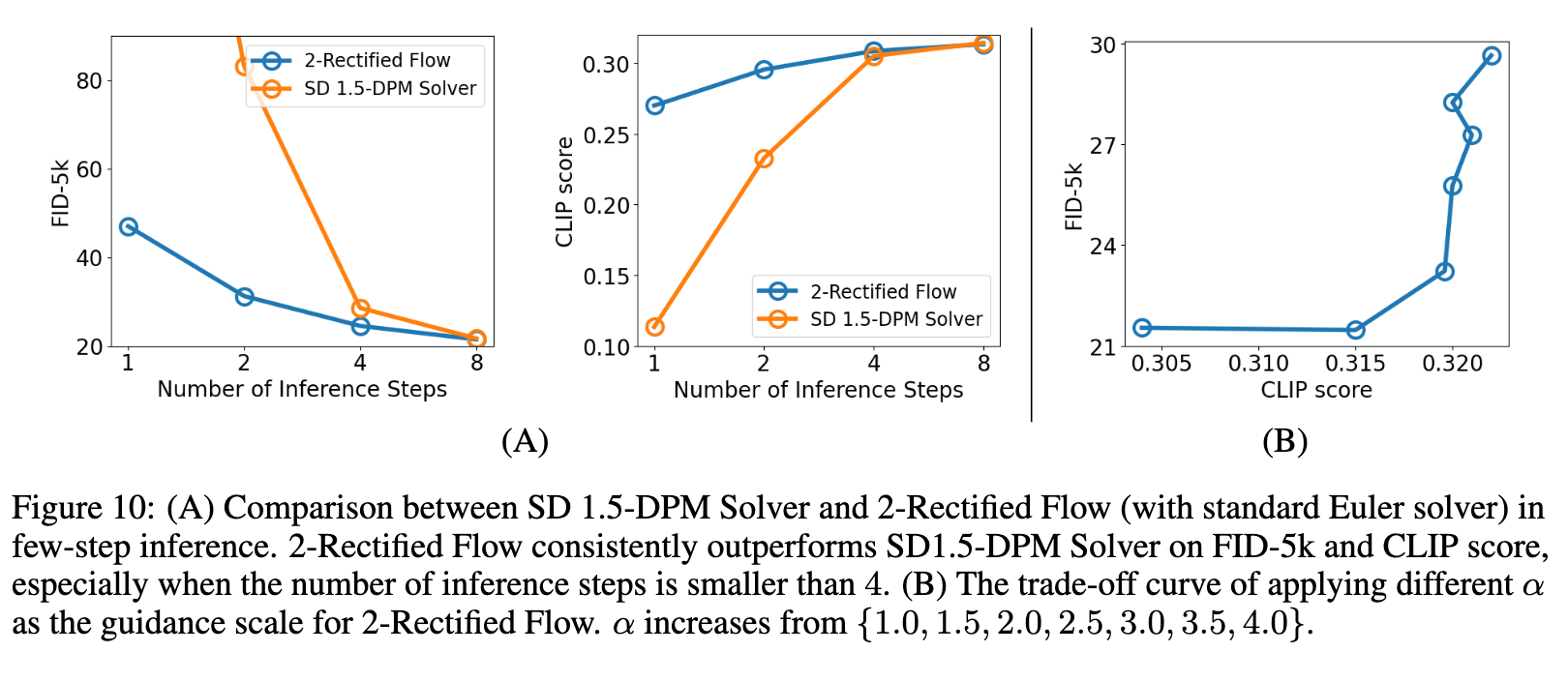
For instance, Stable Diffusion, even when using a state-of-the-art sampler [18, 19, 20], typically requires more than 20 steps to generate acceptable images. The existing one-step large-scale T2I generative models are StyleGAN-T [4] and GigaGAN [11], which rely on generative adversarial training and require careful tuning of both the generator and discriminator. (p. 3)
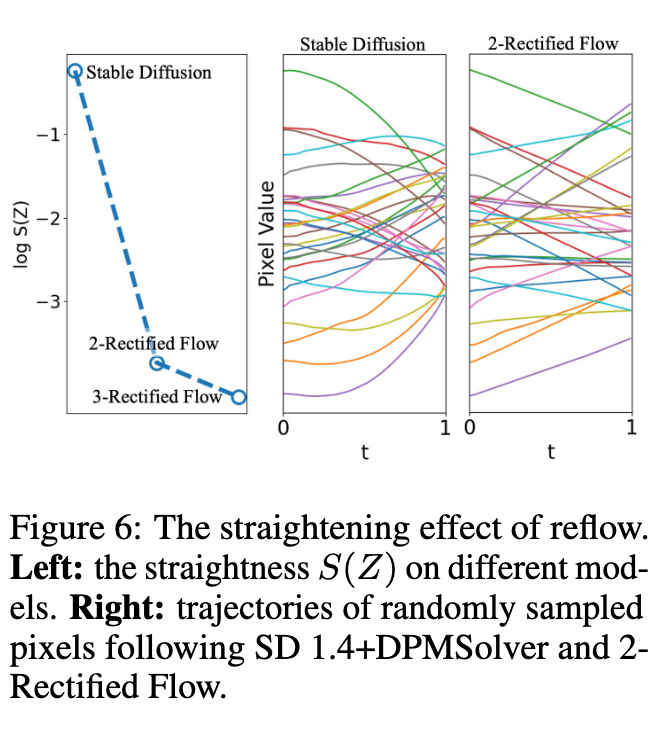
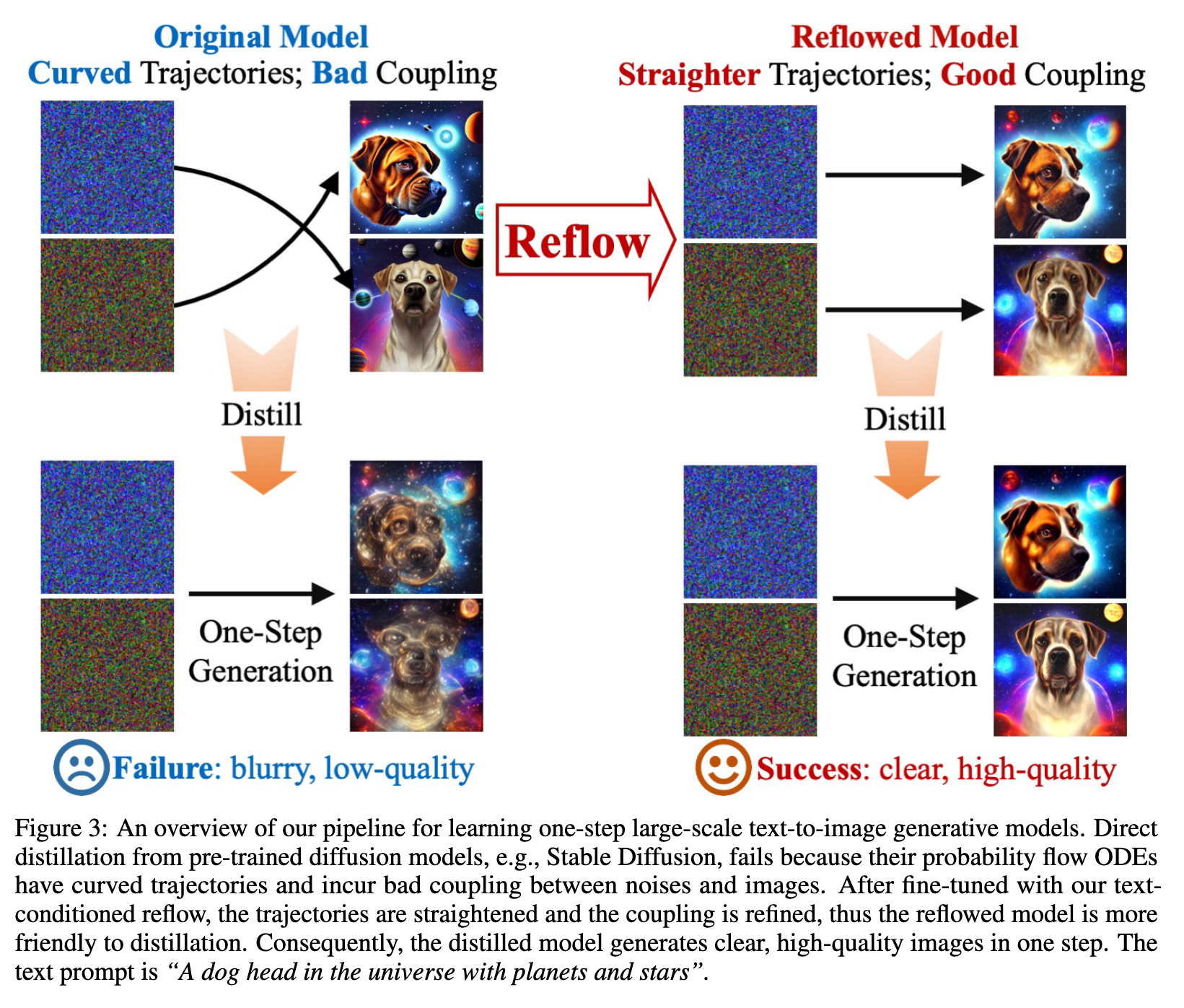
We observed that a straightforward distillation of SD leads to complete failure. The primary issue stems from the sub-optimal coupling of noises and images, which significantly hampers the distillation process. To address this challenge, we leverage Rectified Flow [1, 2], a recent advancement in generative models that utilizes probabilistic flows [17, 23, 24]. In Rectified Flow, a unique procedure known as reflow is employed. Reflow gradually straightens the trajectory of the probability flows, thereby reducing the transport cost between the noise distribution and the image distribution. This improvement in coupling significantly facilitates the distillation process. (p. 3)
Related Work
Recently, [1, 2, 23, 24, 44] propose to directly learn probability flow ODEs by constructing linear or non-linear interpolations between two distributions. These ODEs obtain comparable performance as diffusion models, but require much fewer inference steps. Among these approaches, Rectified Flow [1, 2] introduces a special reflow procedure which enhances the coupling between distributions and squeezes the generative ODE to one-step generation. However, the effectiveness of reflow has only been examined on small datasets like CIFAR10, thus raising questions about its suitability on large-scale models and big data (p. 3)
Despite the impressive generation quality, diffusion models are known to be slow during inference due to the requirement of multiple iterations to reach the final result. To accelerate inference, there are two categories of algorithms. The first kind focuses on fast post-hoc samplers [19, 20, 29, 60, 61, 62]. These fast samplers can reduce the number of inference steps for pre-trained diffusion models to 20-50 steps. However, relying solely on inference to boost performance has its limitations, necessitating improvements to the model itself. Distillation [63] has been applied to pre-trained diffusion models [64], squeezing the number of inference steps to below 10. Progressive distillation [21] is a specially tailored distillation procedure for diffusion models, and has successfully produced 2/4-step Stable Diffusion [3]. Consistency models [22] are a new family of generative models that naturally operate in a one-step manner, but their performance on large-scale text-to-image generation is still unclear (p. 4)
Rectified Flow and Reflow
Rectified Flow [1, 2] is a unified ODE-based framework for generative modeling and domain transfer. It provides an approach for learning a transport mapping T between two distributions π_0 and π_1 on Rd from their empirical observations. In image generation, π_0 is usually a standard Gaussian distribution and π1 the image distribution. Rectified Flow learns to transfer π_0 to π_1 via an ordinary differential equation (ODE), or flow model (p. 5)
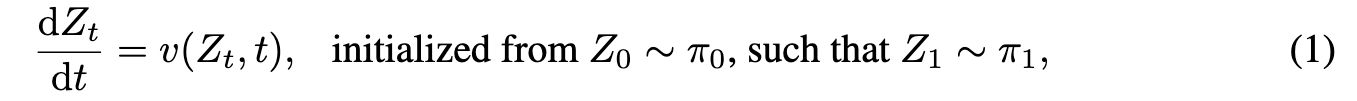
where $v : R^d \times [0, 1] \to R^d$ is a velocity field, learned by minimizing a simple mean square objective: (p. 5)
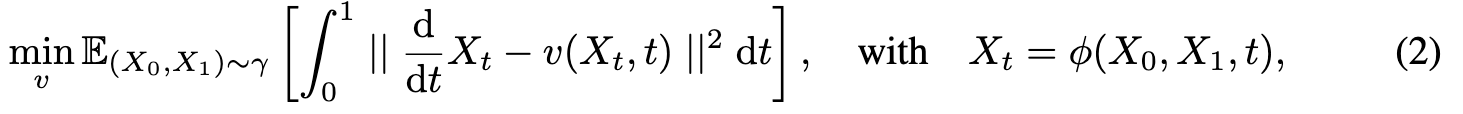
where Xt = ϕ(X_0, X_1, t) is any time-differentiable interpolation between X_0 and X_1, with d dtXt = ∂_t ϕ(X_0, X_1, t). The γ is any coupling of (π_0, π_1). A simple example of γ is the independent coupling γ = π_0 × π_1, which can be sampled empirically from unpaired observed data from π0 and π1. Usually, v is parameterized as a deep neural network and (2) is solved approximately with stochastic gradient methods. (p. 5)
Different specific choices of the interpolation process Xt result in different algorithms. As shown in [1], the commonly used denoising diffusion implicit model (DDIM) [20] and the probability flow ODEs of [17] correspond to Xt = α_t X_0 + β_t X_1, with specific choices of time-differentiable sequences α_t, β_t (see [1] for details). In rectified flow, however, the authors suggested a simpler choice of (p. 5)

which favors straight trajectories that play a crucial role in fast inference, as we discuss in sequel. (p. 5)
Straight Flows Yield Fast Generation
In practice, the ODE in (1) need to be approximated by numerical solvers. The most common approach is the forward Euler method, which yields (p. 5)
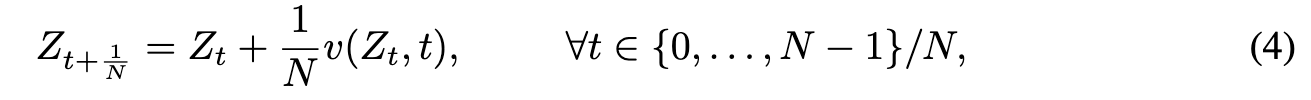
For fast simulation, it is desirable to learn the ODEs that can be simulated accurately and fast with a small N. This leads to ODEs whose trajectory are straight lines. Specifi- cally, we say that an ODE is straight (with uniform speed) if (p. 5)
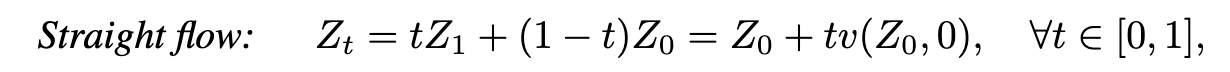

Straightening via Reflow
A reflow step turns vk into a new vector field vk+1 that yields straighter ODEs while Xnew 1 = ODEvk+1 has the same distribution as X1 = ODEvk, (p. 6)
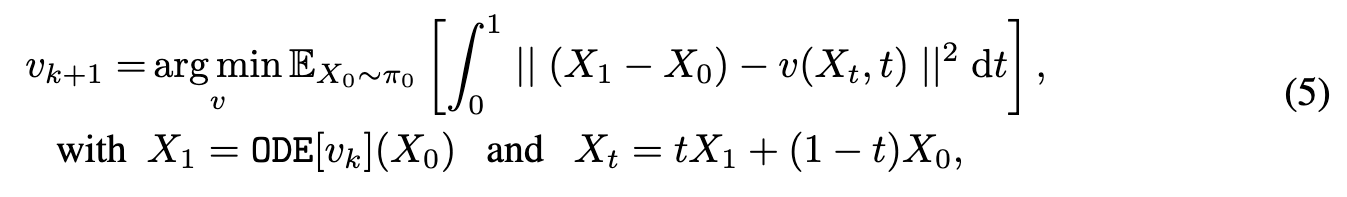
The key property of reflow is that it preserves the terminal distribution while straightening the particle trajectories and reducing the transport cost of the transport mapping:
- The distribution of $ODEv_{k+1}$ and $ODEv_k$ coincides; hence v_{k+1} transfers π_0 to π_1 if v_k does so.
- The trajectories of $ODE[v_{k+1}]$ tend to be straighter than that of ODE[v_k]. This suggests that it requires smaller Euler steps N to simulate $ODE[v_{k+1}]$ than ODE[v_k]. If v_k is a fixed point of reflow, that is, $v_{k+1} = v_k$, then ODE[v_k] must be exactly straight.
- $(X_0, ODEv_{k+1})$ forms a better coupling than $(X_0, ODEv_k)$ in that it yields lower convex transport costs, that is, $E[c(ODEv_{k+1}− X_0)] \leq E[c(ODEv_k− X_0)]$ for all convex functions c : R_d → R. This suggests that the new coupling might be easier for the network to learn. (p. 6)
Text-Conditioned Reflow
In text-to-image generation, the velocity field v should additionally depend on an input text prompt T to generate corresponding images. (p. 6)
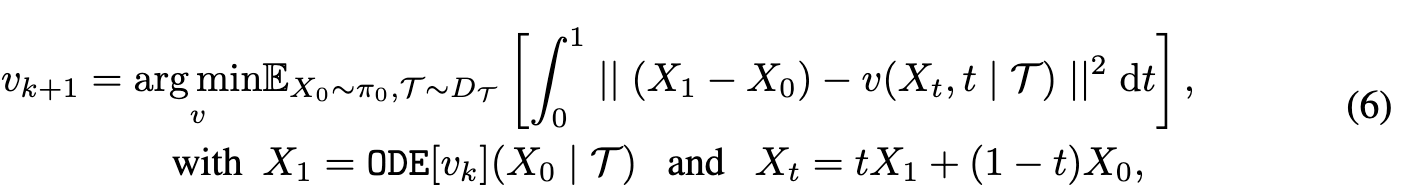
Distillation
Fortunately, it was observed in [1] that the trajectories of ODE[v_k] becomes nearly (even though not exactly) straight with even one or two steps of reflows. With such approximately straight ODEs, one approach to boost the performance of one-step models is via distillation: (p. 7)
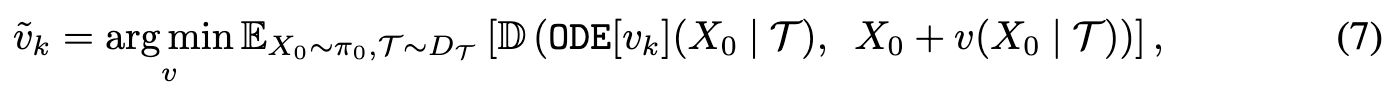
| where we learn a single Euler step x+v(x | T ) to compress the mapping from X0 to $ODE[v_k](X_0 | \tau )$ by minimizing a differentiable similarity loss D(·, ·) between images. Following [1, 21, 22], we adopt the Learned Perceptual Image Patch Similarity (LPIPS) loss [65] as the similiarty loss since it results in higher visual quality and better quantitative results. Learning one-step model with distillation avoids adversarial training [4, 11, 66] or special invertible neural networks [67, 68, 69]. (p. 7) |
| It is essential to use reflow to get good coupling before applying distillation. It is important to note the difference between distillation and reflow: while distillation tries to honestly approximate the mapping from X0 to $ODE[v_k](X_0 | \tau )$, reflow yields a new mapping $ODE[v_{k+1}](X_0 | \tau )$ that can be more regular and smooth due to lower convex transport costs. In practice, we find that it is essential to apply reflow to make the mapping $ODE[v_k](X_0 | \tau )$ sufficiently regular and smooth before applying distillation. (p. 7) |
Classifier-Free Guidance Velocity Field for Rectified Flow
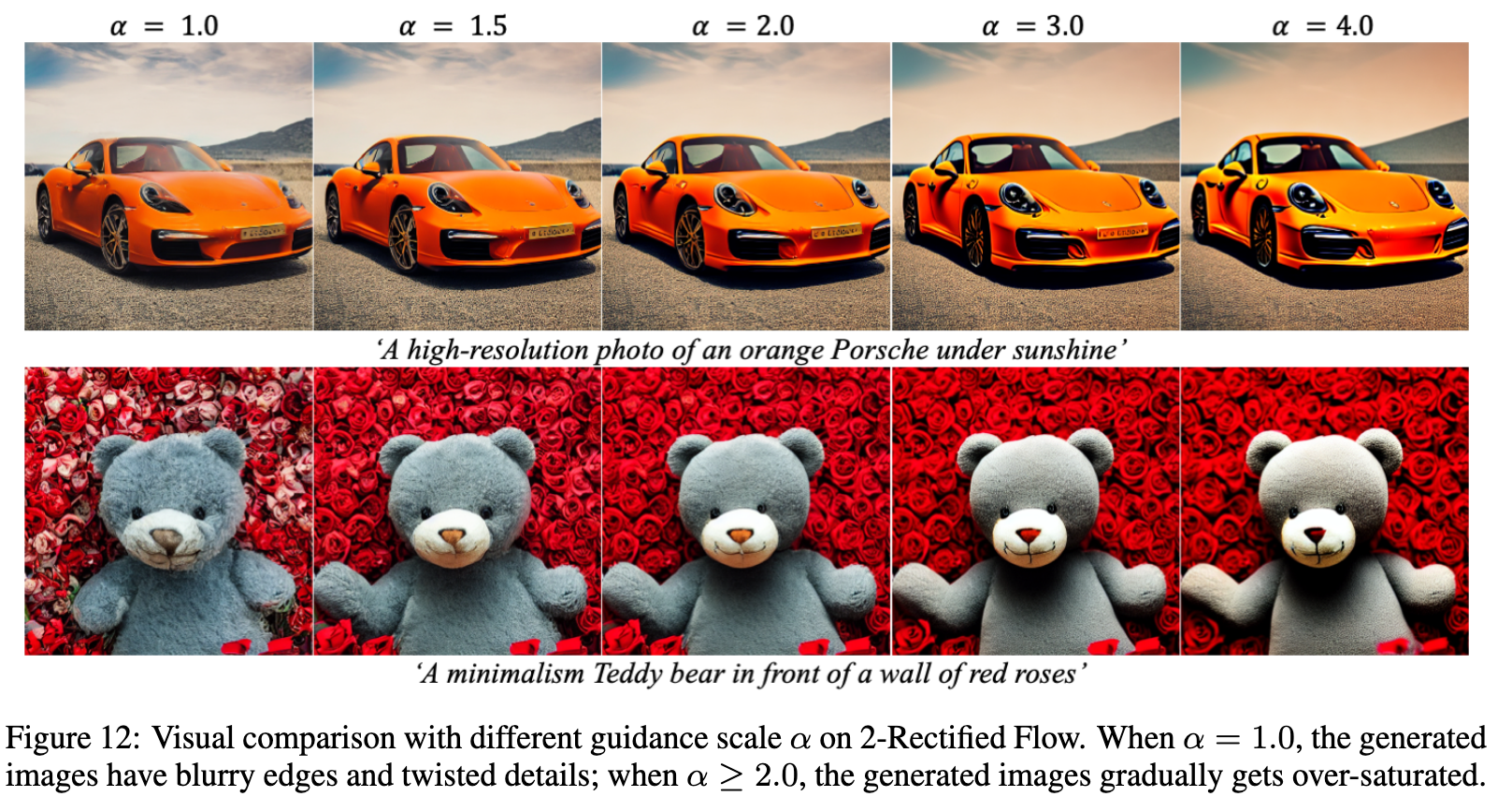
Similarly, we can define the following velocity field to apply Classifier-Free Guidance on the learned Rectified Flow, (p. 7)
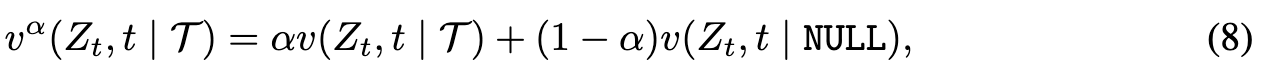
Experiment