Llemma An Open Language Model For Mathematics
[llm tool deep-learning llama math proof lemma This is my reading note for Llemma: An Open Language Model For Mathematics. This paper proposes to continue the training of code llama on math dataset to improve its performance on math problem.
Introduction
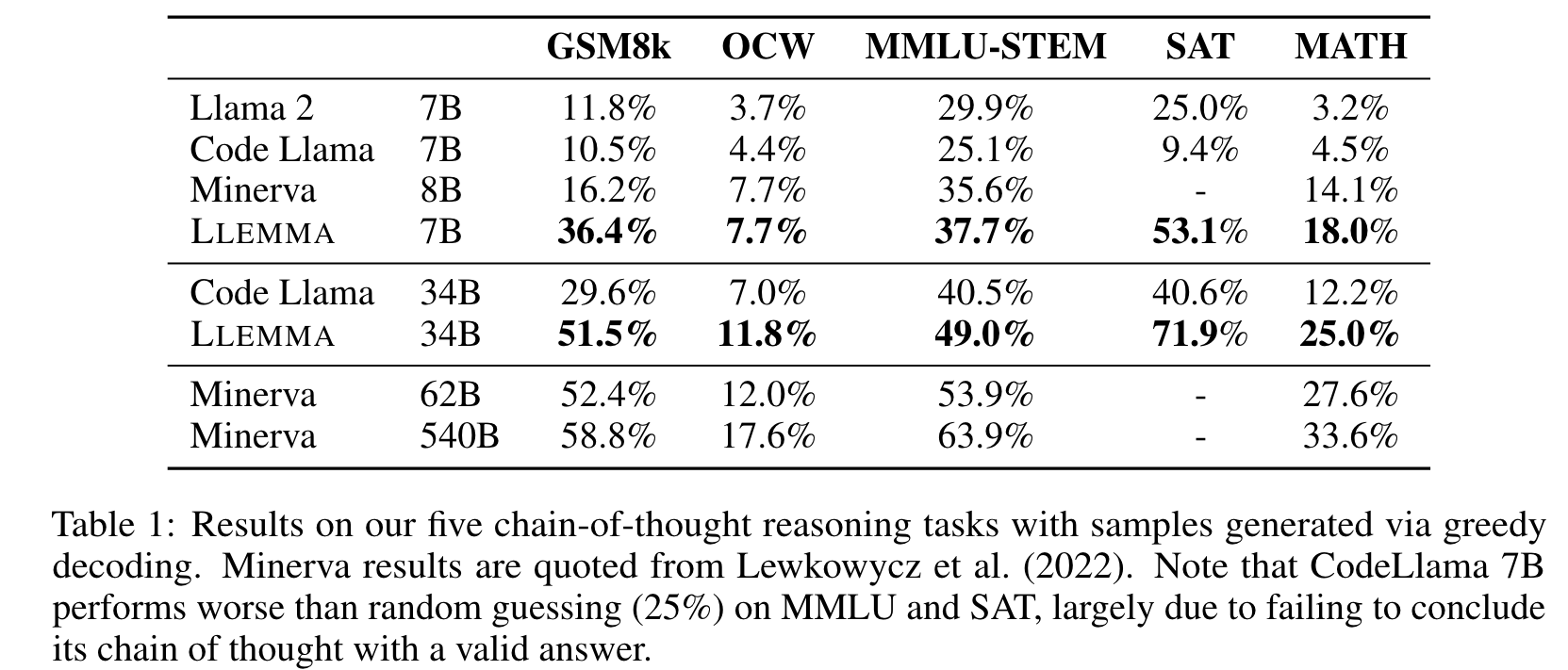
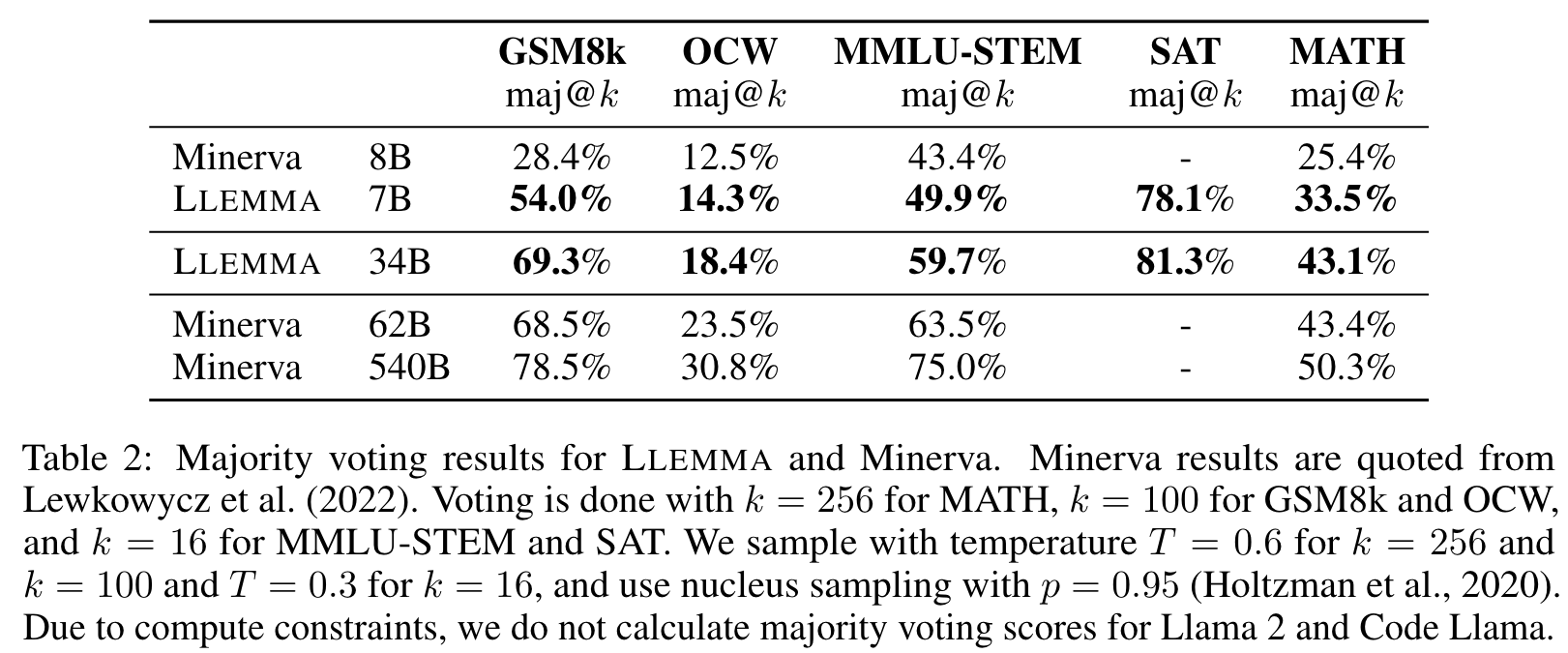
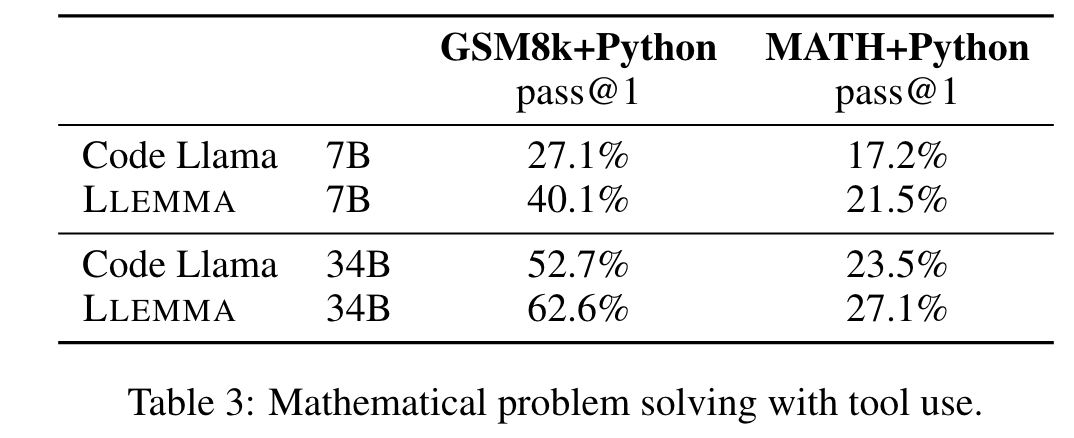
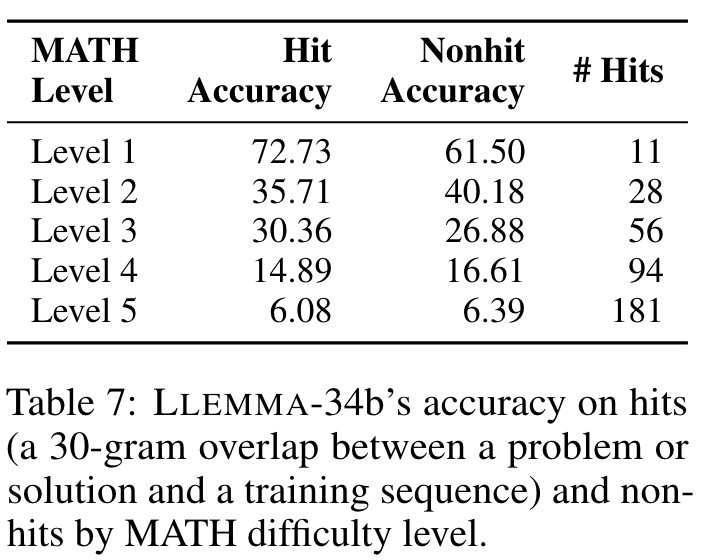
We present LLEMMA, a large language model for mathematics. We continue pretraining Code Llama on Proof-Pile-2, a mixture of scientific papers, web data containing mathematics, and mathematical code, yielding LLEMMA. Moreover, LLEMMA is capable of tool use and formal theorem proving without any further finetuning. (p. 1)
- First, solving mathematical problems requires pattern matching against a large body of specialized prior knowledge, thus serving as an ideal setting for domain adaptation.
- Second, mathematical reasoning is in itself a central AI task (p. 1)
- Third, language models capable of strong mathematical reasoning are upstream of a number of research topics, such as reward modeling (Uesato et al., 2022; Lightman et al., 2023), reinforcement learning for reasoning (Polu et al., 2022; Lample et al., 2022), and algorithmic reasoning (Zhou et al., 2022; Zhang et al., 2023). (p. 1)
We present a recipe for adapting a language model to mathematics through continued pretraining (Lewkowycz et al., 2022; Rozière et al., 2023) on Proof-Pile-2, a diverse mixture of math-related text and code. Applying the recipe to Code Llama (Rozière et al., 2023) yields LLEMMA: 7 billion and 34 billion parameter base language models with substantially improved mathematical capabilities (p. 2)
APPROACH
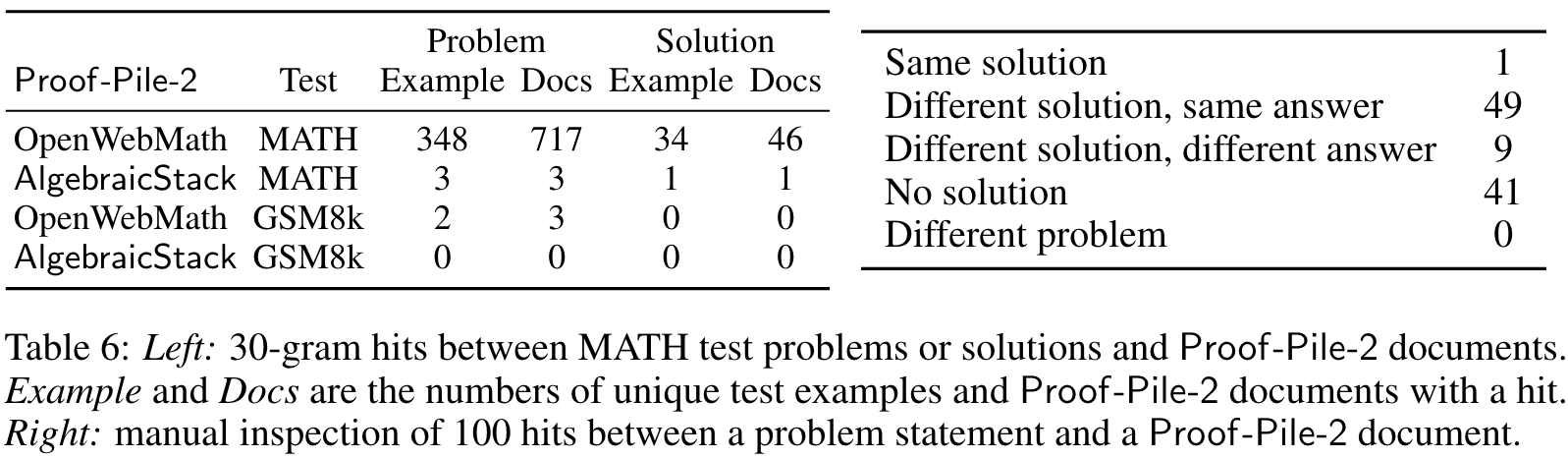
DATA: Proof-Pile-2

MODEL AND TRAINING
We train the 7B model for 200B tokens, and the 34B model for 50B tokens. (p. 3)
We train all models in bfloat16 mixed precision using the GPT-NeoX library (Andonian et al., 2023) across 256 A100 40GB GPUs. We use Tensor Parallelism (Shoeybi et al., 2019) with a world size of 2 for LLEMMA-7B , and a world size of 8 for LLEMMA-34B, alongside ZeRO Stage 1 sharded optimizer states (Rajbhandari et al., 2020) across Data Parallel (Goyal et al., 2017) replicas. We use Flash Attention 2 (Dao, 2023) to improve throughput and further reduce memory requirements. (p. 3)
LLEMMA 7B is trained for 42, 000 steps with a global batch size of 4 million tokens and a 4096 token context length. This corresponds to roughly 23, 000 A100-hours. The learning rate is warmed up to 1 · 10−4 over 500 steps, then set to cosine decay to 1/30th of the maximum learning rate over 48, 000 steps. (p. 3) %%0.84 epoch over the 200B dataset.%%
LLEMMA 34B is trained for 12, 000 steps with a global batch size of 4 million tokens and a 4096 context length. This corresponds to roughly 47, 000 A100-hours. The learning rate is warmed up to 5 · 10−5 over 500 steps, then decayed to 1/30th the peak learning rate. (p. 3)
Before training LLEMMA 7B, we contract the RoPE (Su et al., 2022) base period of the Code Llama 7B initialization from θ = 1, 000, 000 to θ = 10, 000. This is so that the long context finetuning procedure described in Peng et al. (2023)and Rozière et al. (2023) can be repeated on the trained LLEMMA 7B (we leave actually doing so to future work). Due to compute constraints, we were unable to verify that training LLEMMA 34B with a contracted RoPE base period did not come with a performance penalty, therefore for that model we preserved θ = 1, 000, 000. (p. 3)
EVALUATION