MeshDiffusion Score-based Generative 3D Mesh Modeling
[dream-booth signed-distance-function diffusion read sdf gan score-distillation-sampling deep-learning style-gan tet-gan mesh tetrahedral marching-cube dmtet This is my reading note for MeshDiffusion: Score-based Generative 3D Mesh Modeling. This paper represents the 3D mesh as a reformed tetrahedral which is defined on a regular 3D grid with 4 channel features: 3D positional deformation of the vertex and signed distance function values to define the surface.
Introduction
To overcome these shortcomings, we take advantage of the graph structure of meshes and use a simple yet very effective generative modeling method to generate 3D meshes. Specifically, we represent meshes with deformable tetrahedral grids, and then train a diffusion model on this direct parametrization. both voxels and point clouds are relatively hard for artists to edit. Moreover, modern graphics pipelines are built and optimized for explicit geometry representations like meshes (p. 2)
However, SDFs are typically harder to learn as it requires a carefully designed sampling strategy and regularization. Because SDFs are usually parameterized with multi-layer perceptrons (MLPs) in which a smoothness prior is implicitly embedded, the generated shapes tend to be so smooth that sharp edges and important (and potentially semantic) details are lost. Moreover, SDFs are costly to render and therefore less suitable for downstream tasks like conditional generation with RGB images, which require an efficient differentiable renderer during inference (p. 2)
However, it is by no means a trivial task and poses two critical problems: (1) the numbers of vertices and faces are indefinite for general object categories, and (2) the underlying topology varies wildly and edges have to be generated at the same time (p. 2)
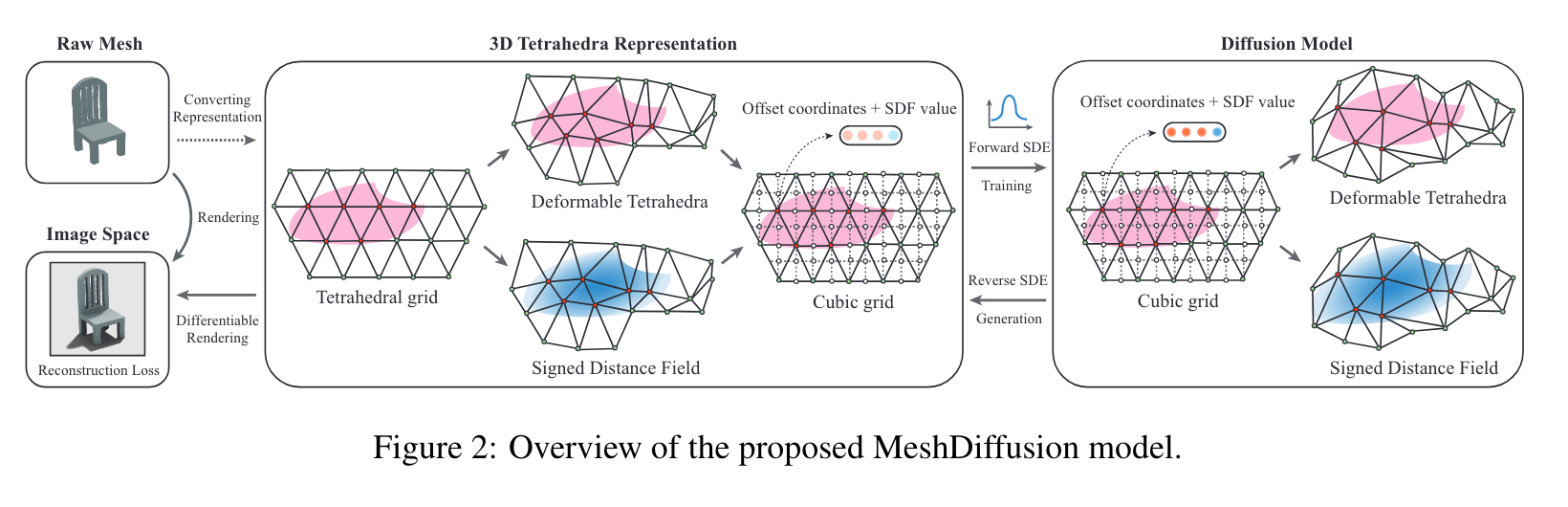
One common approach is to discretize the 3D space and encapsulate each mesh in a tiny cell, and it is proven useful in simulation [37] and human surface modeling. we propose to train diffusion models on a discretized and uniform tetrahedral grid structure which parameterizes a small yet representative family of meshes. With such a grid representation, topological change is subsumed into the SDF values and the inputs to the diffusion model now assume a fixed and identical size. (p. 2)
RELATED WORK
3D Shape Generation
[33] extends this approach to the topology-varying case with autoregressive models, sequentially generating vertices and edges, but it is hardly scalable and yields unsatisfactory results on complex geometry. [13] which uses StyleGAN [19] with a differentiable renderer on tetrahedral grid representations and learns to generate 3D meshes from 2D RGB images, TetGAN [14] which trains generative adversarial networks (GANs) on tetrahedral grids and LION [54] which uses a trained Shape-As-Points [36] network to build meshes from diffusion-model-generated latent point clouds. (p. 3)
Mesh Reconstruction
One of the most popular methods is marching cubes [29] which assumes that a surface is represented by the zero level set of some continuous field, and this continuous field can be well approximated by linear interpolation of discrete grid point. By assuming the points lie on a surface, one can build triangular meshes by connecting these points, a process known as Delaunay triangulation (p. 3)
PRELIMINARIES
Deep marching tetrahedra (DMTet) [43] is a method to parametrize and optimize meshes of arbitrary topology in a differentiable way. The 3D space is discretized with a deformable tetrahedral grid, in which each vertex possesses a SDF value. The SDF of each 3D position in the space is computed by marching tetrahedra [12], which assumes SDF values to be barycentric interpolation of the SDF values of the vertices of the enclosing tetrahedra (p. 3)
MeshDiffusion: DIFFUSION MODEL ON MESHES
As a result, our model takes as input a uniform tetrahedral grid with 4-dimensional attributes (specifically, 3 dimensions are for deformation and 1 dimension is for SDF). These structural priors inspire us to use 3D convolutions. (p. 4)
TRAINING OBJECTIVE
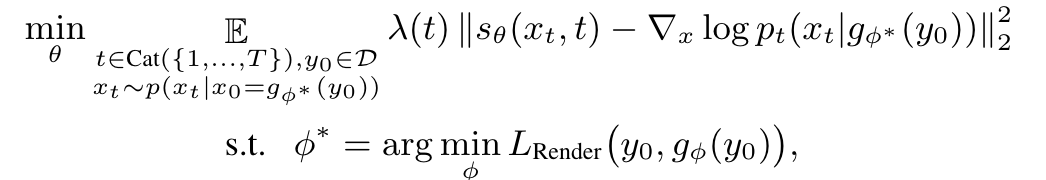

g_φ(y_0) is the mapping from 2D views of y0 to its tetrahedral grid representation and LRender is the rendering (and relevant regularization) loss used in [32]. However, we notice that with RGB images only, it fails to learn some complex geometries, especially when surface materials are highly specular. To (p. 5)
REDUCING NOISE EFFECT OF MARCHING TETRAHEDRA
Recall that the triangular mesh vertex position vp on a single tetrahedron edge e = (a, b) is computed by linear interpolation vp = (v_a s_b − v_b s_a)/(s_b − s_a), in which v_a, v_b are the positions of tetrahedron vertices a and b, and s_a, s_b are the corresponding SDF values. (p. 5)
EXPERIMENTS AND RESULTS
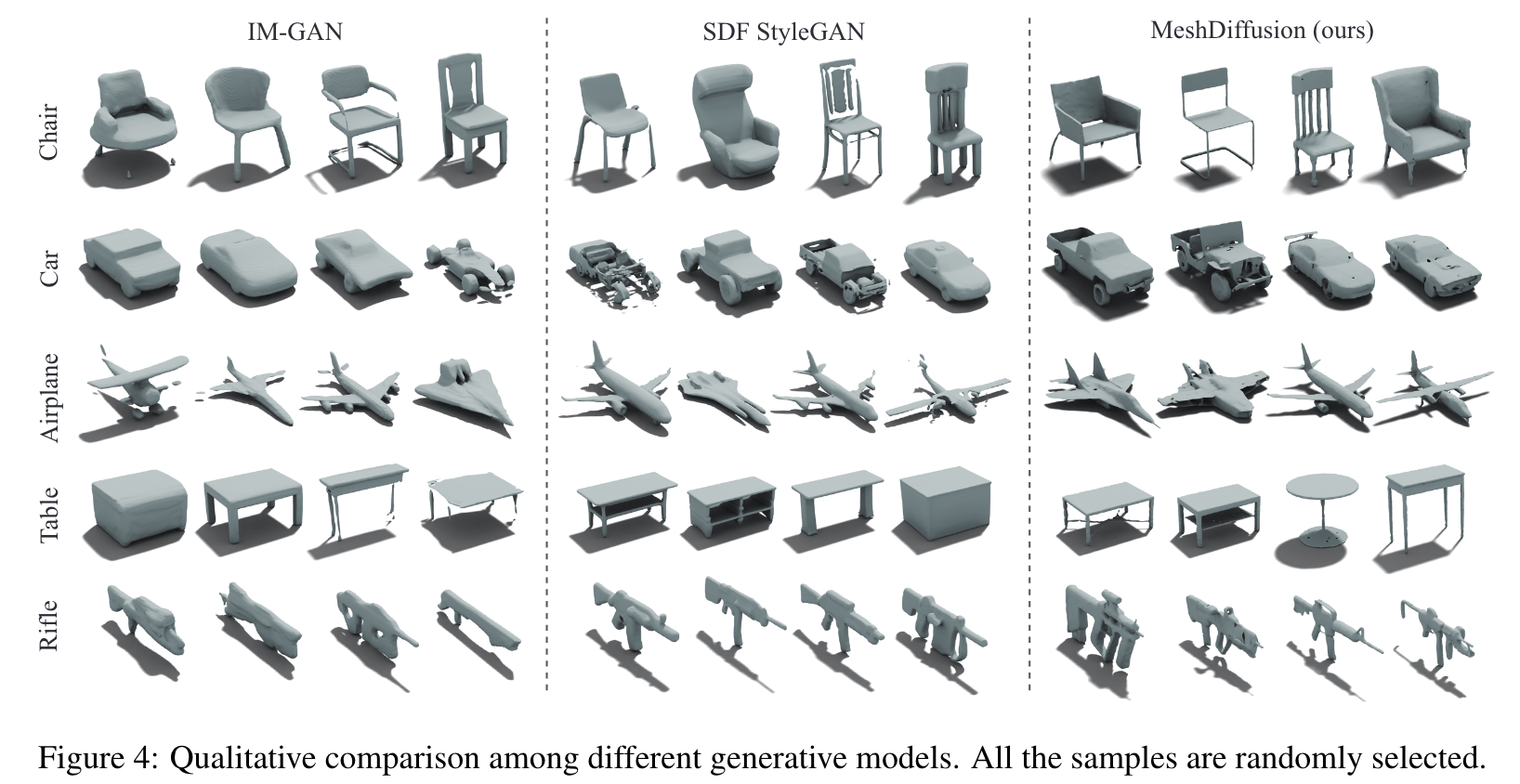

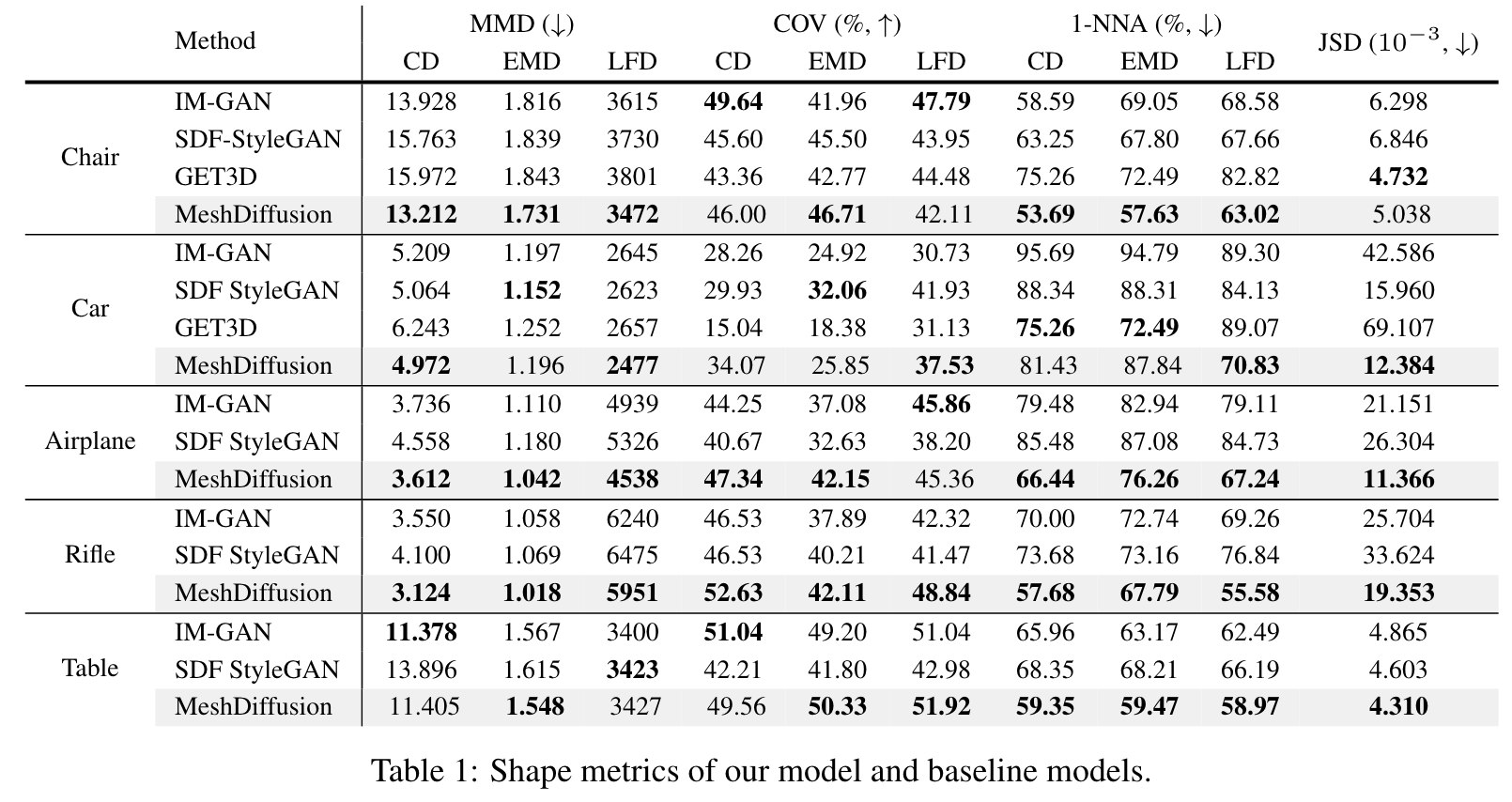
For ablation on alternative architectures, we train GANs on our datasets with an architecture similar to the one used in [51]. Our SDF-based baselines include IM-GAN [9] and SDF-StyleGAN [55]. We also compare MeshDiffusion against GET3D [13] which also uses DMTet for mesh parametrization. (p. 7)
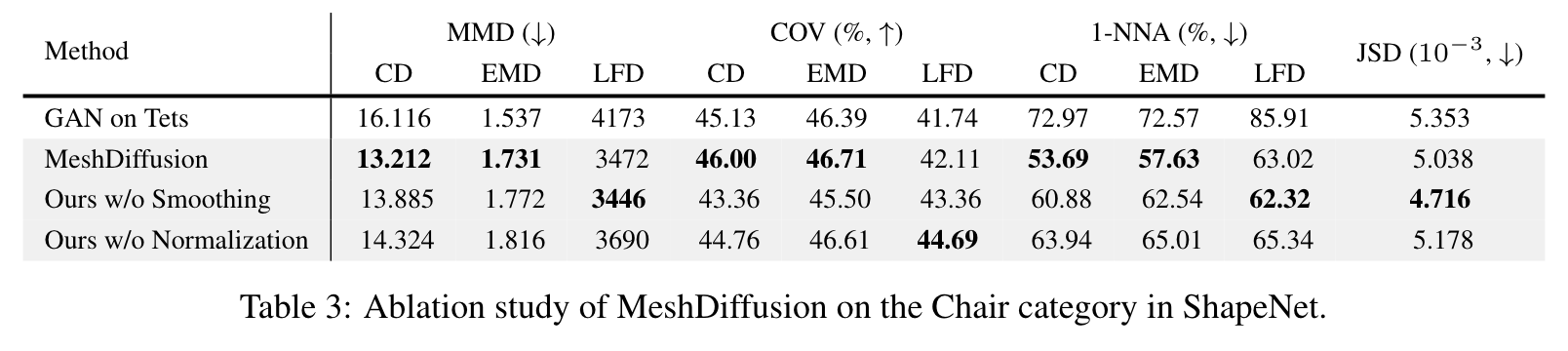
Additionally, we perform ablation study on the choices of models in Table 3. It can be observed that the our SDF normalization strategy described in Section 4.3 is indeed beneficial for the diffusion model, and our customized diffusion model is better suited for our mesh generation setting. (p. 8)
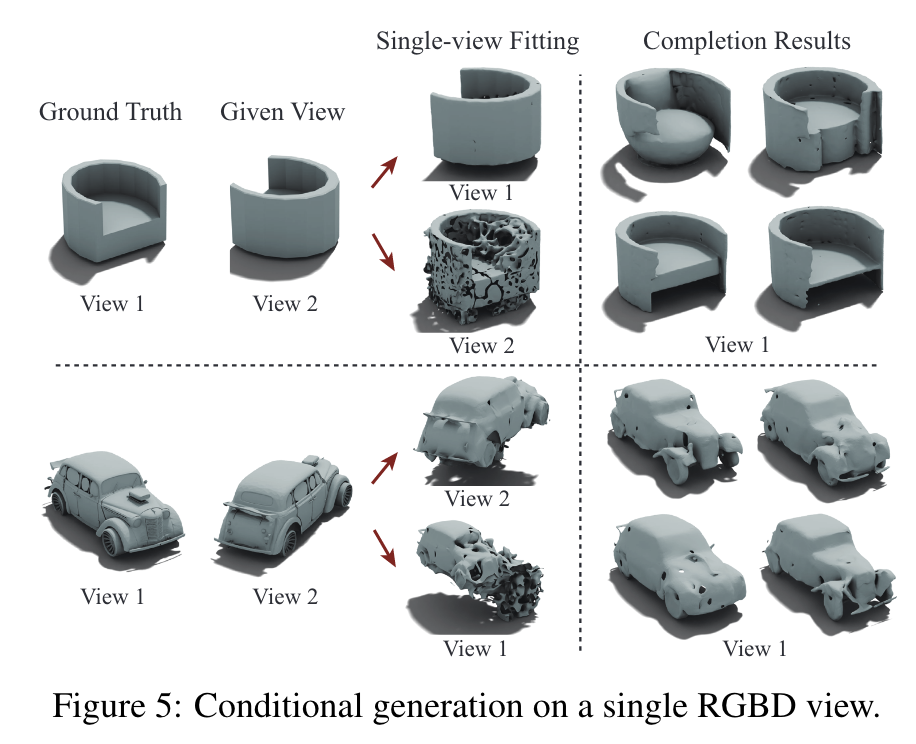
Because the geometry estimated from the single-view fitting is not perfect even in the given single view, we allow the originally-fixed tetrahedral vertices to be slightly updated by the diffusion model near the end of the diffusion completion process (p. 8)
DISCUSSIONS
Optimization issues with DMTet
While DMTet is capable of fitting geometries, it fails in cases where the underlying topology is complex. Besides, it is not encouraged to learn the true topology of shapes and may produce invisible topological holes by contracting the neighboring triangular mesh vertices close enough. Furthermore, we observe that the optimization process with differentiable rasterization of 3D meshes may produce floating and isolated meshes, especially when depth supervision is introduced. It is therefore worth designing better optimization techniques, regularization methods and possibly better parametrization of meshes for the purpose of training mesh diffusion models. (p. 9)

Diffusion model design
Our experiments demonstrate the effectiveness of the simple design with few hyperparameter and architecture changes: a 3D-CNN-based UNet on augmented cubic grids with DDPM. (p. 9)
Limitations
Diffusion model typically assumes a known dataset in the input modality (augmented tetrahedral grids in our case), but to efficiently train diffusion models on 2D images, we need a better way to amortize the costs and fully leverage the power of differentiable rendering. Our paper avoids this important aspect but instead adopts the twostage approach of “reconstruction-then-generation”. Moreover, in our formulation, the differentiable renderer is useful only during the tetrahedral grid creation process, while in principle we believe there can be ways to incorporate the differentiable render in the training and inference process of diffusion models. Finally, our diffusion model is built with a very naïve architecture, thus limiting the resolution of input tetrahedral grids, while we notice that some of the fine details cannot be fully captured with the current resolution of 64 during the dataset creation stage. With better architecture designs or adaptive resolution techniques (as in [43]), we may greatly increase the resolution and generate a more diverse set of fine-level geometric details. (p. 9)
