Encoding Method for NERF
[sinusoid-encoding multi-resolution cnn mlp nerf deep-learning hash-encoding differential-rendering frequency-encoding Instant Neural Graphics Primitives with a Multiresolution Hash Encoding tries to reduce inference cost with a versatile new input encoding that permits the use of a smaller network without sacrificing quality. This is achieved via a small neural network is augmented by a multiresolution hash table of trainable feature vectors whose values are op- timized through stochastic gradient descent.
Existing Encoding Methods
In my note nerf, to make sure the NERF could generate enough details and high quality results, it applies frequency (sinusoid) encoding to the input (position and orientation), which maps each of it to a 2L vector.
\[\gamma(p)=(sin(2^0\pi p),cos(2^0\pi p),\cdots,sin(2^{L-1}\pi p),cos(2^{L-1}\pi p))\]Müller et al. [2019; 2020] suggested a continuous variant of the one-hot encoding based on rasterizing a kernel, the one-blob encoding, which can achieve more accurate results than frequency encodings in bounded domains at the cost of being single-scale.
Parametric encodings. Recently, state-of-the-art results have been achieved by parametric encodings which blur the line between classical data structures and neural approaches. The idea is to arrange additional trainable parameters (beyond weights and biases) in an auxiliary data structure, such as a grid [Chabra et al. 2020; Jiang et al. 2020; Liu et al. 2020; Mehta et al. 2021; Peng et al. 2020a; Sun et al. 2021; Tang et al. 2018; Yu et al. 2021a] or a tree [Takikawa et al. 2021], and to look-up and (optionally) interpolate these parameters depending on the input vector \(x\in\mathbb{R}^d\). This arrangement trades a larger memory footprint for a smaller computational cost.
Another parametric approach uses a tree subdivision of the domain \(x\in\mathbb{R}^d\), wherein a large auxiliary coordinate encoder neural net- work (ACORN) [Martel et al. 2021] is trained to output dense feature grids in the leaf node around x.
Sparse parametric encodings. While existing parametric encodings tend to yield much greater accuracy than their non-parametric predecessors, they also come with downsides in efficiency and versatility. Dense grids oftrainable features consume much more memory than the neural network weights. Alternatively, sparse encoding could be leveraged, if the surface of interest is known a priori.
Proposed Encoding Methods
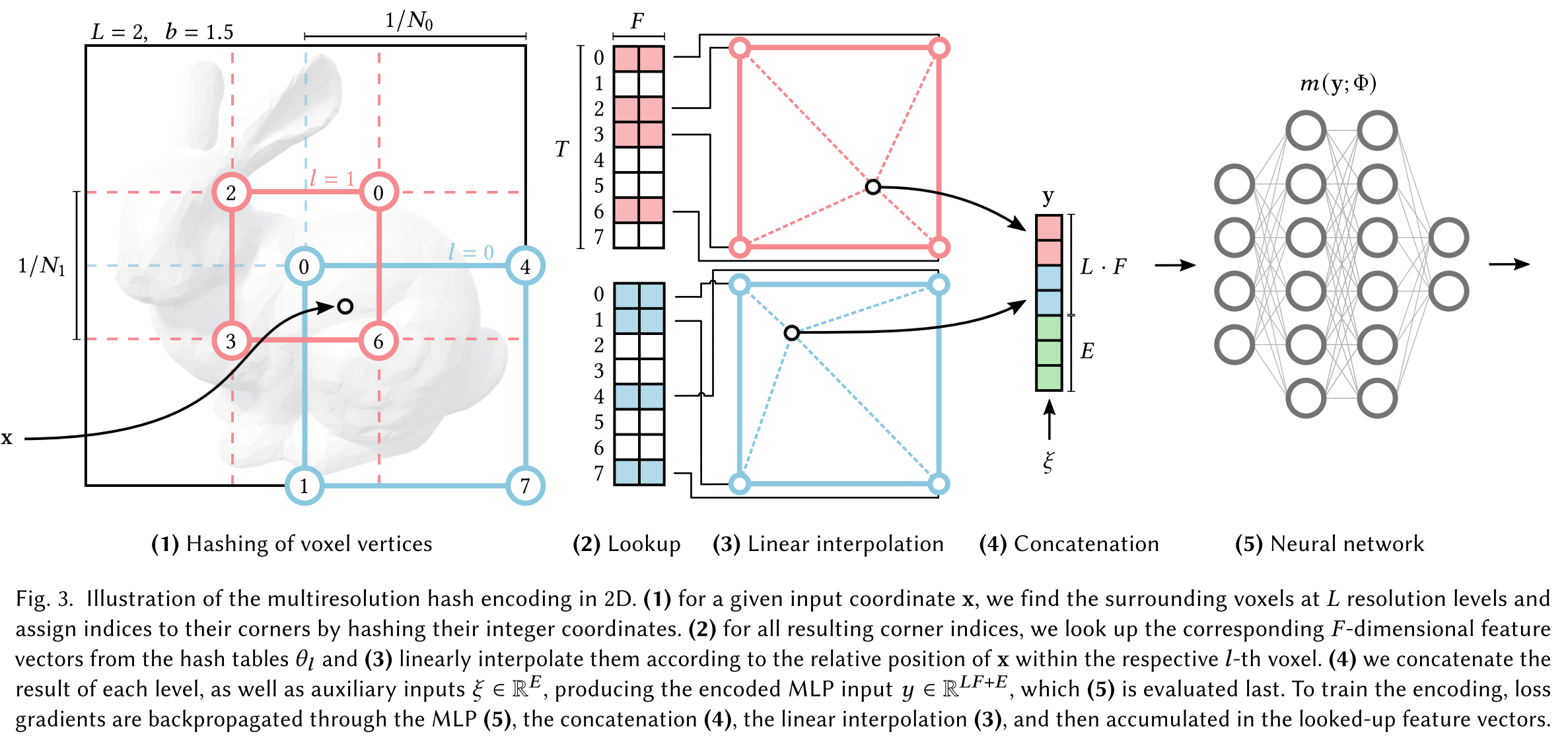
As illustraded in the fiture above, we store the trainable feature vectors in a compact spatial hash table, whose size is a hyperparameter T which can be tuned to trade the number of parameters for reconstruction quality. It doesn’t requires the surface of interest is known.
Analogous to the multi-resolution grid in (d), we use multiple (L) separate hash tables indexed at different resolutions, whose interpolated outputs are concatenated before being passed through the MLP. The reconstruction quality is comparable to the dense grid encoding, despite having 20× fewer parameters.
We rely on the neural network to learn to disambiguate hash collisions itself, avoiding control flow divergence, reducing implementation complexity and improving performance. Another performance benefit is the predictable memory layout of the hash tables that is independent of the data that is represented.
Our neural network not only has trainable weight parameters \(\Phi\), but also trainable encoding parameters \(\theta\). These are arranged into L levels, each containing up to T feature vectors with dimensionality F. Experiments suggest L=16 and F=2 could be a good choice.
To be more specific, each level contains features of up to T vertices of grid, which is tracked by a hash table. Lastly, the feature vectors at each corner are d-linearly interpo-lated according to the relative position of x to the vertices of its hypercube.
Results
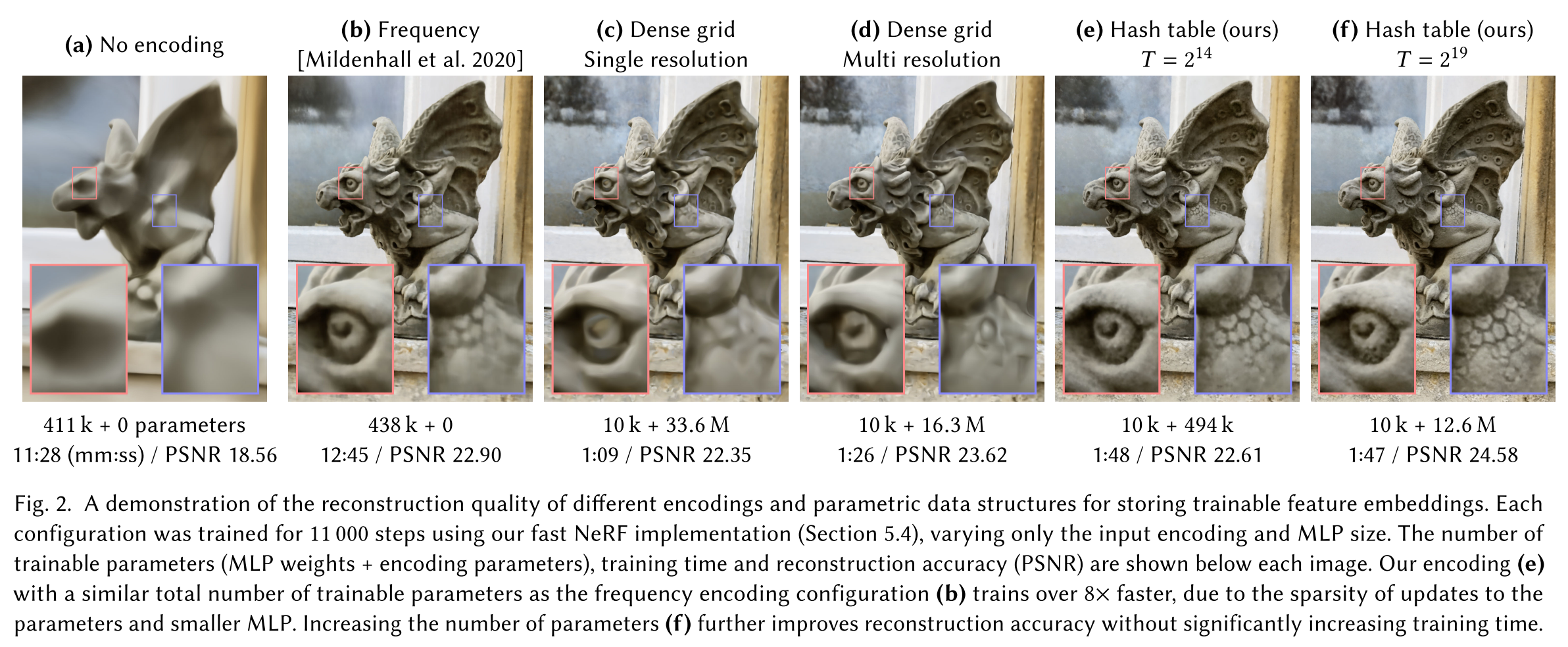
The experiment result is shown below. Obviously, the proposed methods (e and f) generates more details than all the other approaches.