The Impact of Depth and Width on Transformer Language Model Generalization
[llm transformer deep-learning width depth This is my reading note for The Impact of Depth and Width on Transformer Language Model Generalization. This paper shows that deeper transformer is necessary to have a good performance. Usually 4 to 6 layers is a good choice.
Introduction
We report three main conclusions:
- after fine-tuning, deeper models generalize better out-of-distribution than shallower models do, but the relative benefit of additional layers diminishes rapidly;
- within each family, deeper models show better language modeling performance, but returns are similarly diminishing;
- the benefits of depth for compositional generalization cannot be attributed solely to better performance on language modeling or on in-distribution data. (p. 1)
METHODOLOGY
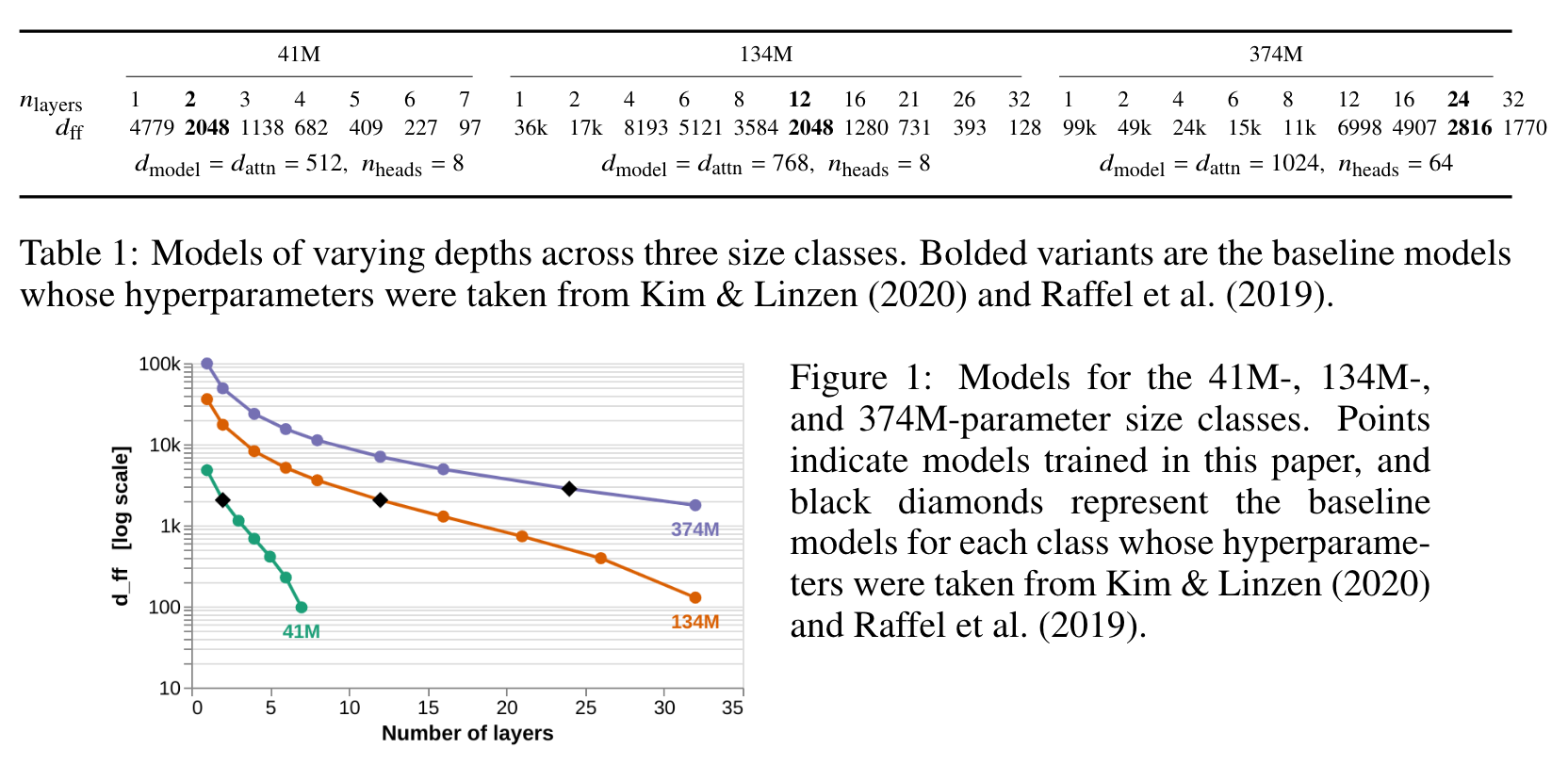
CONSTRUCTING FAMILIES OF MODELS WITH EQUAL NUMBERS OF PARAMETERS
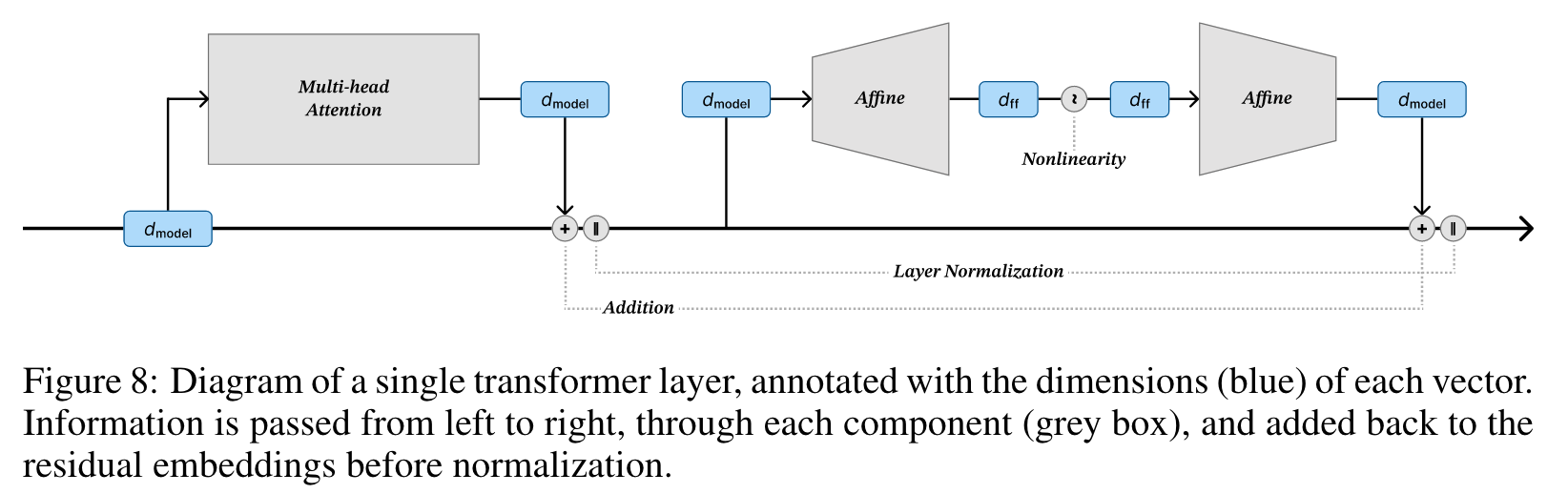
we can reduce the size of the feed-forward dimension 𝑑_ff, reduce the size of the residual stream (the embedding size) 𝑑_model, or reduce the size of the attention outputs 𝑑_attn (see Appendix B for a diagram of a transformer layer annotated with dimensionality labels). Vaswani et al. (2017) coupled these three variables at 𝑑_model = 𝑑_attn = 𝑑_ff/4. (p. 2)
RESULTS
LANGUAGE MODELING
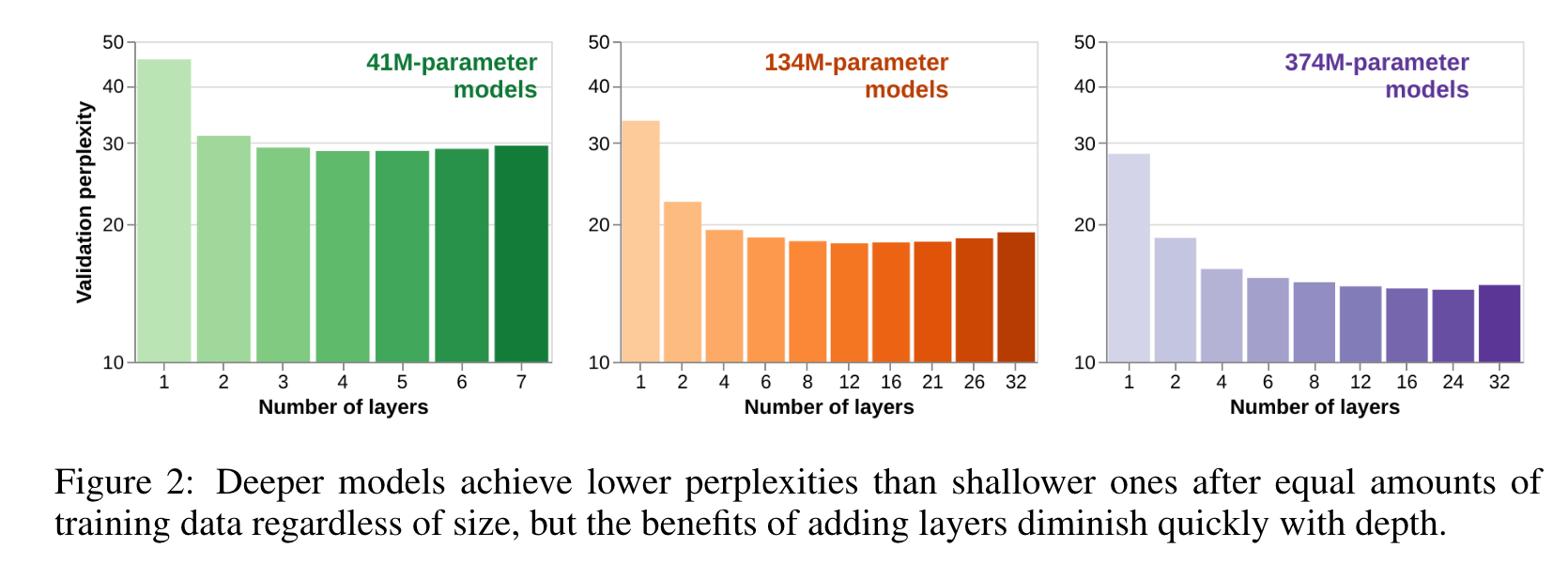
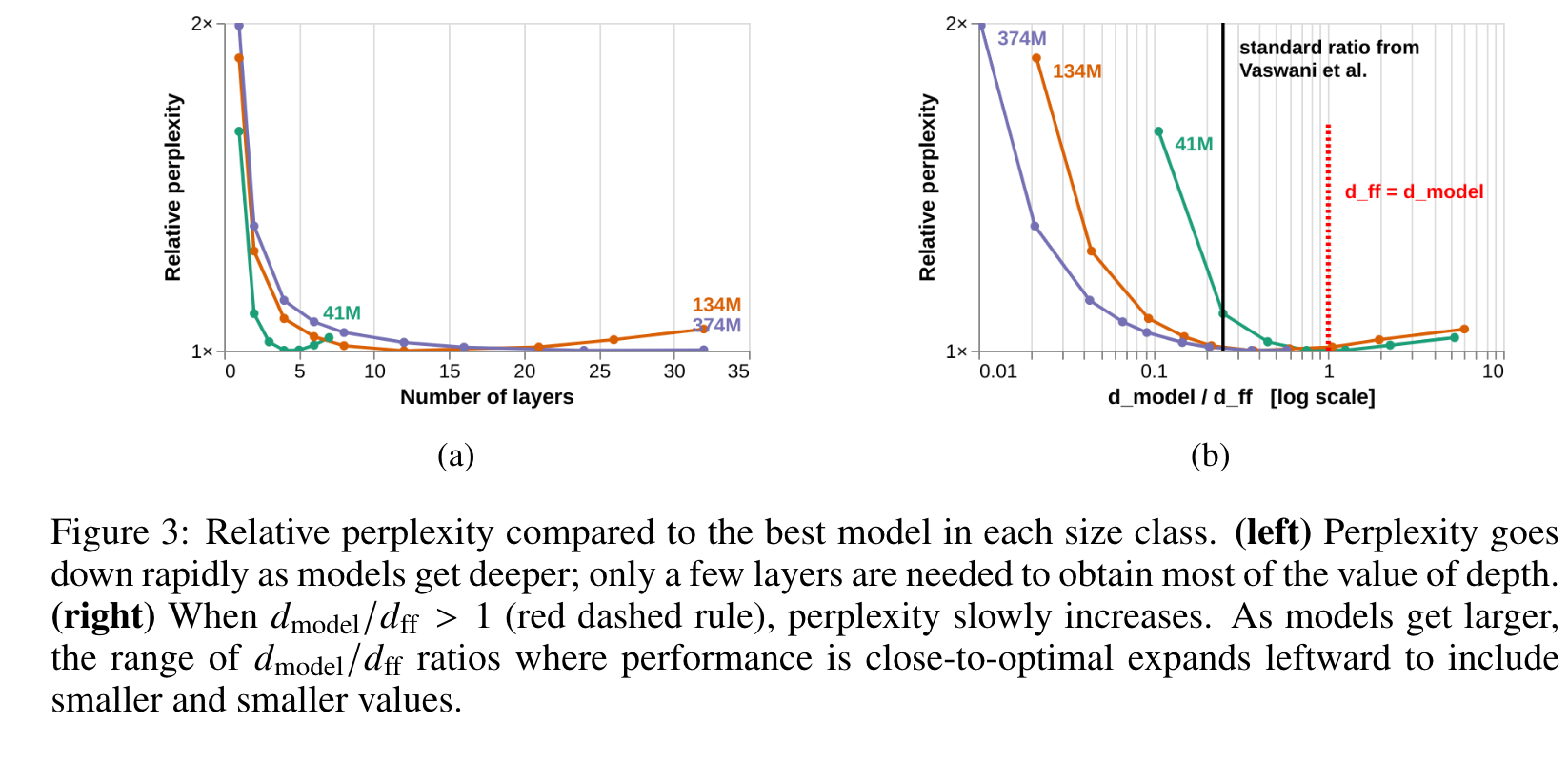
- While deeper models do, in general, perform better than shallower ones, the increase in performance that comes from adding layers diminishes rapidly as models become deeper (Figure 3a). (p. 4)
- At the deeper end of our scale, adding layers is not only unhelpful for performance, but begins to harm it (see the right-hand sides of each size-class curve in Figure 3a). (p. 5)
- We find that smaller models are more sensitive to the particular value of the feed-forward ratio, and that for small models the standard ratio may not be optimal. This shows that larger models have more leeway to trade depth for width, becoming wider in proportion to their model dimension 𝑑model without incurring large penalties for their perplexity. It also shows that when 𝑑model/𝑑ff < 1 the feedforward ratio no longer serves as a predictor of relative perplexity independent of size. (p. 5)
COMPOSITIONAL GENERALIZATION
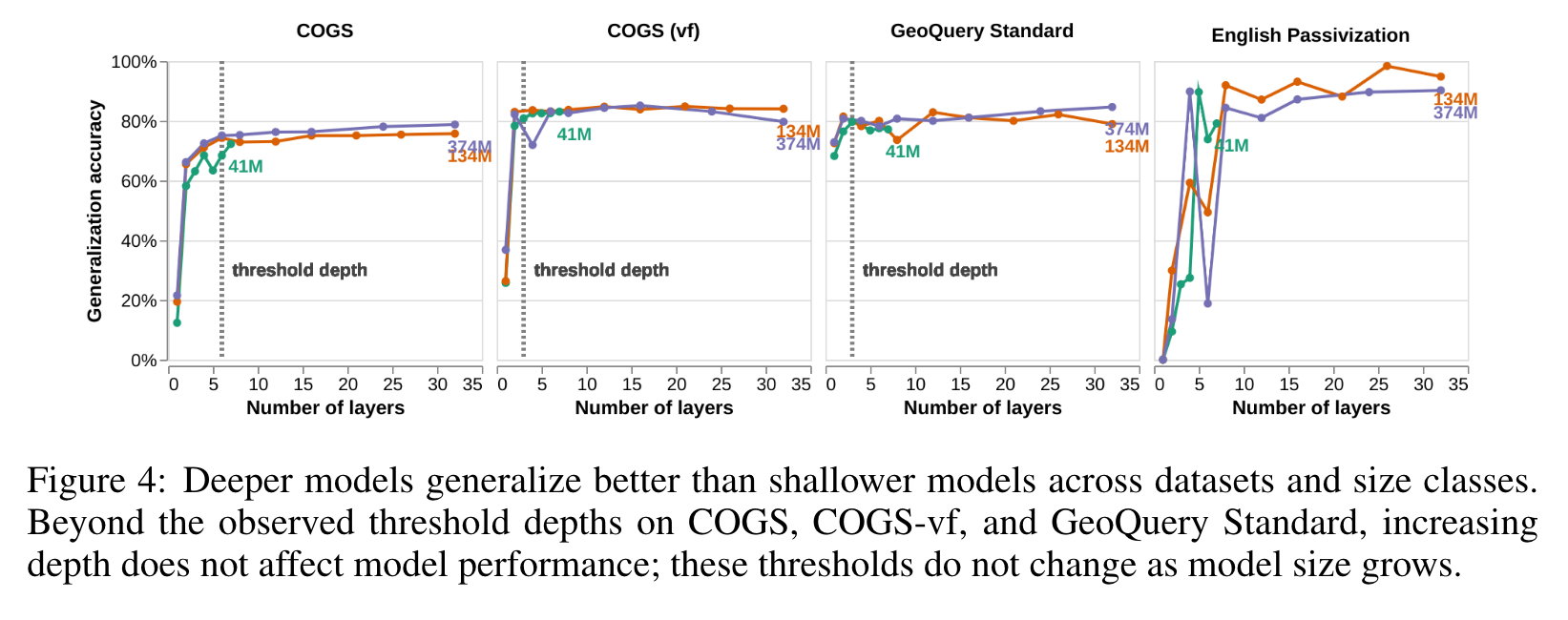
- On each of the datasets, deeper models tend to attain higher generalization accuracies than shallower models in the same size class. (p. 6)
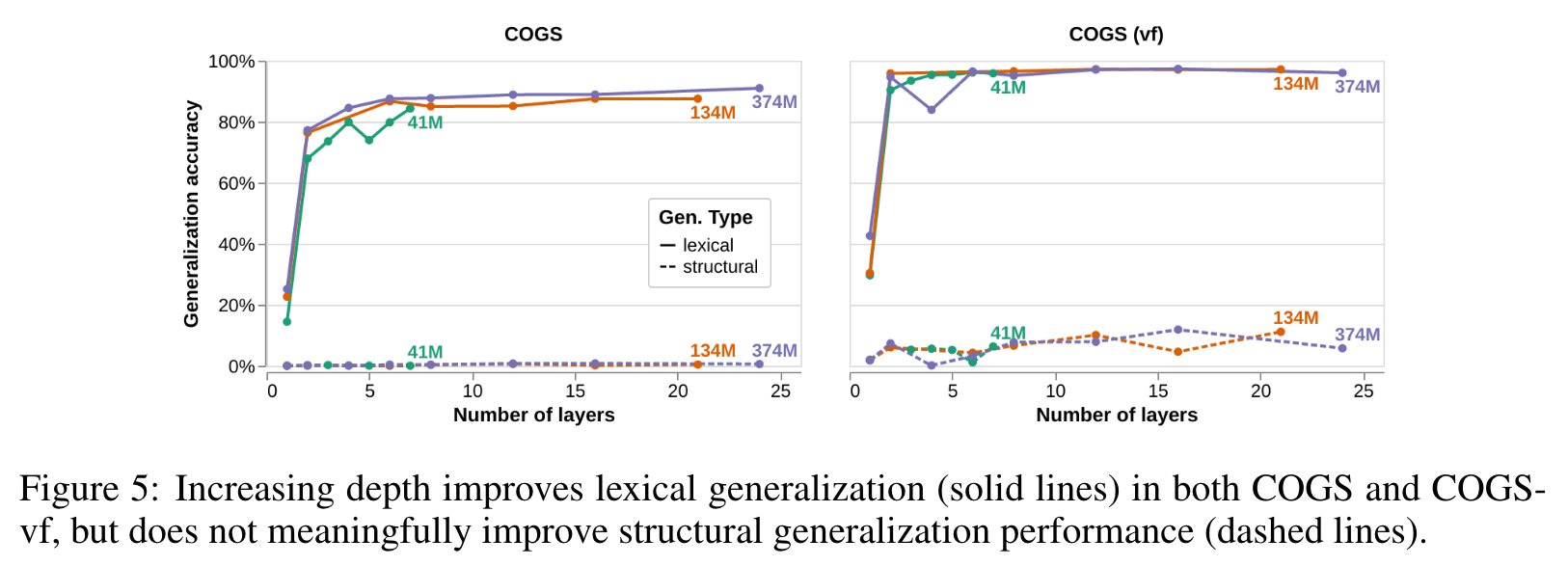
- As with language modeling, most of the benefit of depth is gained by having only a few layers. This supports the hypothesis that the saturated effect of depth is due to the existence of easier subsets of the datasets, and shows that increasing depth alone does substantially improve the models’ ability to learn the correct inductive bias for these structural tasks (p. 6)
THE EFFECT OF DEPTH ON GENERALIZATION IS NOT SOLELY ATTRIBUTABLE TO BETTER PRETRAINING LOSS OR IN-DISTRIBUTION PERFORMANCE
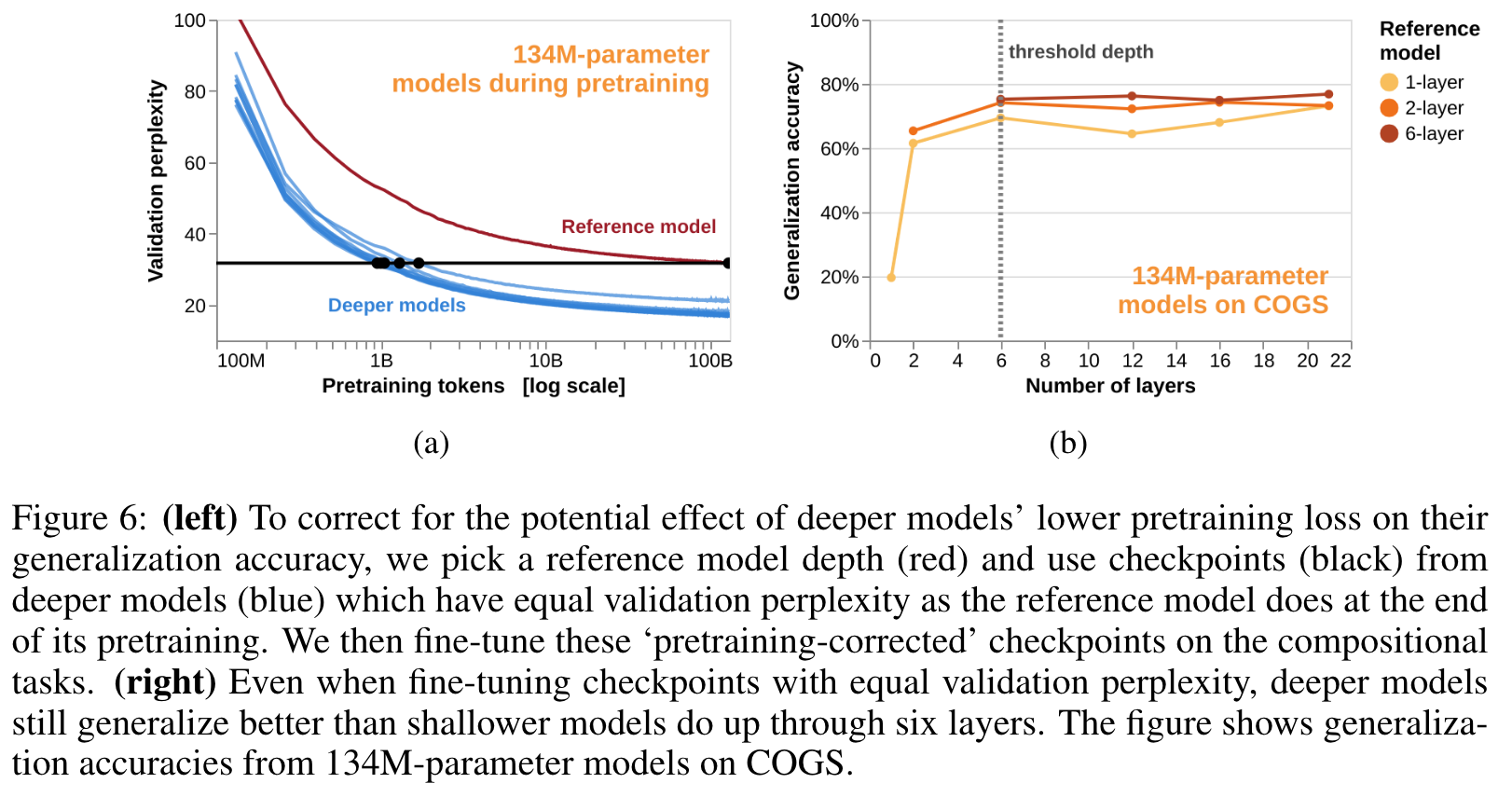
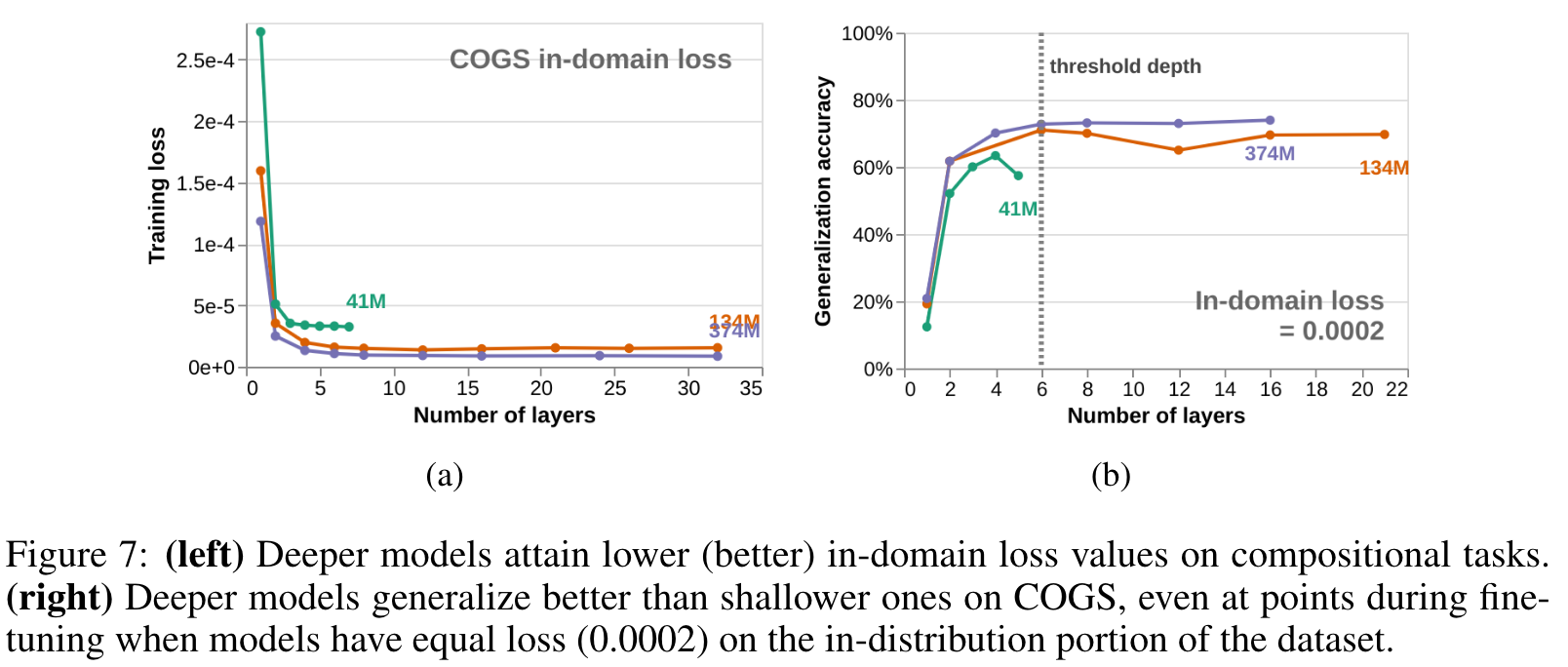
- Both of these observations are potential confounds for the interpretation of the previous section: perhaps depth does not directly improve generalization accuracy, but only does so indirectly by allowing models to either become better LMs or else to better learn the in-distribution fine-tuning data (p. 7)
Written on October 31, 2023
