Diff-Instruct A Universal Approach for Transferring Knowledge From Pre-trained Diffusion Models
[kl-divergence diffusion gan distill score-distillation-sampling deep-learning dreamfusion This is my reading note on Diff-Instruct: A Universal Approach for Transferring Knowledge From Pre-trained Diffusion Models. The paper explains the theory of using a pre-trained diffusion model to guide the training of a generator model.it shows that both DreamFusion and GAN are a special case of it: score distillation sampling (SDS) from DreamFusion uses Dirac distribution to represent the generator while GAN learns a discriminator to represents the distribution of data. To this end, it proposes IKL, which is tailored for DMs by calculating the integral of the KL divergence along a diffusion process (instead of a single step), which we show to be more robust in comparing distributions with misaligned supports.
Introduction
Containing intricate information about data distributions, pre-trained DMs are valuable assets for downstream applications. In this work, we consider learning from pre-trained DMs and transferring their knowledge to other generative models in a data-free fashion. Specifically, we propose a general framework called Diff-Instruct to instruct the training of arbitrary generative models as long as the generated samples are differentiable with respect to the model parameters. Our proposed Diff-Instruct is built on a rigorous mathematical foundation where the instruction process directly corresponds to minimizing a novel divergence we call Integral Kullback-Leibler (IKL) divergence. IKL is tailored for DMs by calculating the integral of the KL divergence along a diffusion process, which we show to be more robust in comparing distributions with misaligned supports. We also reveal non-trivial connections of our method to existing works such as DreamFusion [56], and generative adversarial training. To (p. 1)
Currently, we are witnessing a rising trend of learning from models, especially when accessing large amounts of high-quality data is difficult. Such a model-driven learning scheme can be particularly appealing for handling new tasks by providing a solid base model, which can be further improved by additional training data (p. 2)
DMs represent a class of explicit generative models wherein the data’s score function is modeled. Conversely, in various downstream applications, implicit generative models are favored due to their inherent flexibility and efficiency. An implicit model typically learns a neural transformation (i.e., a generator) that maps from a latent space to the data space, such as in generative adversarial networks (GANs), thereby enabling expeditious generation. (p. 2)
For implicit models that lack explicit score information, how to receive supervision from DM’s multi-level score network is technically challenging, which greatly limits the potential use cases of pre-trained DMs (p. 2)
Our proposed Diff-Instruct is built on a rigorous mathematical foundation where the instruction process directly corresponds to minimizing a novel divergence we call Integral Kullback-Leibler (IKL) divergence. IKL is tailored for DMs by calculating the integral of the KL divergence along a diffusion process, which we show to be more robust in comparing distributions with misaligned supports (Section 3.2). We also reveal non-trivial connections of our method to existing works such as DreamFusion (Section 3.3.1) and generative adversarial training (Section 3.3.2). Interestingly, we show that the SDS objective can be seen as a special case of our Diff-Instruct on the scenario that the generator outputs a Dirac’s Delta distribution. (p. 2)
Preliminary
Currently, DMs are the most powerful explicit models while GANs are the most powerful implicit models. (p. 3)
Diffusion model ties to optimize the following loss:
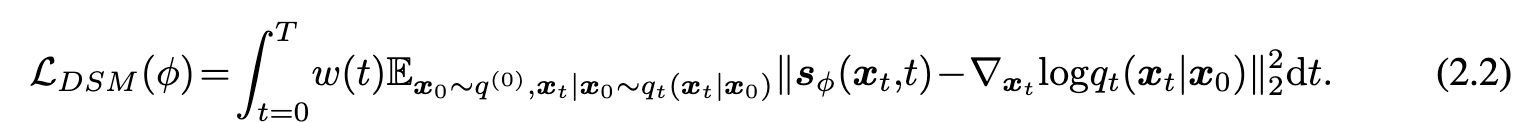where a multiple-level or continuous-indexed score network $s_\phi(x,t)$ is usually employed in order to approximate marginal score functions of the forward diffusion process
GAN ties to optimize the following loss:
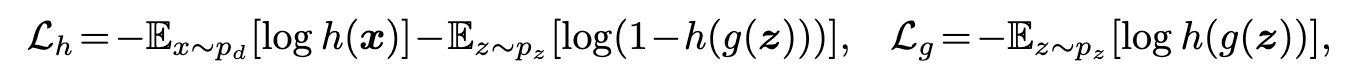where l_h is the discriminator loss and l_g is the generator loss. They leverage neural networks (generators) to map an easy-to-sample latent vector to generate a sample. Therefore they are efficient. However, the training of GANs is challenging, particularly because of the reliance on adversarial training (p. 3)
Proposed Method
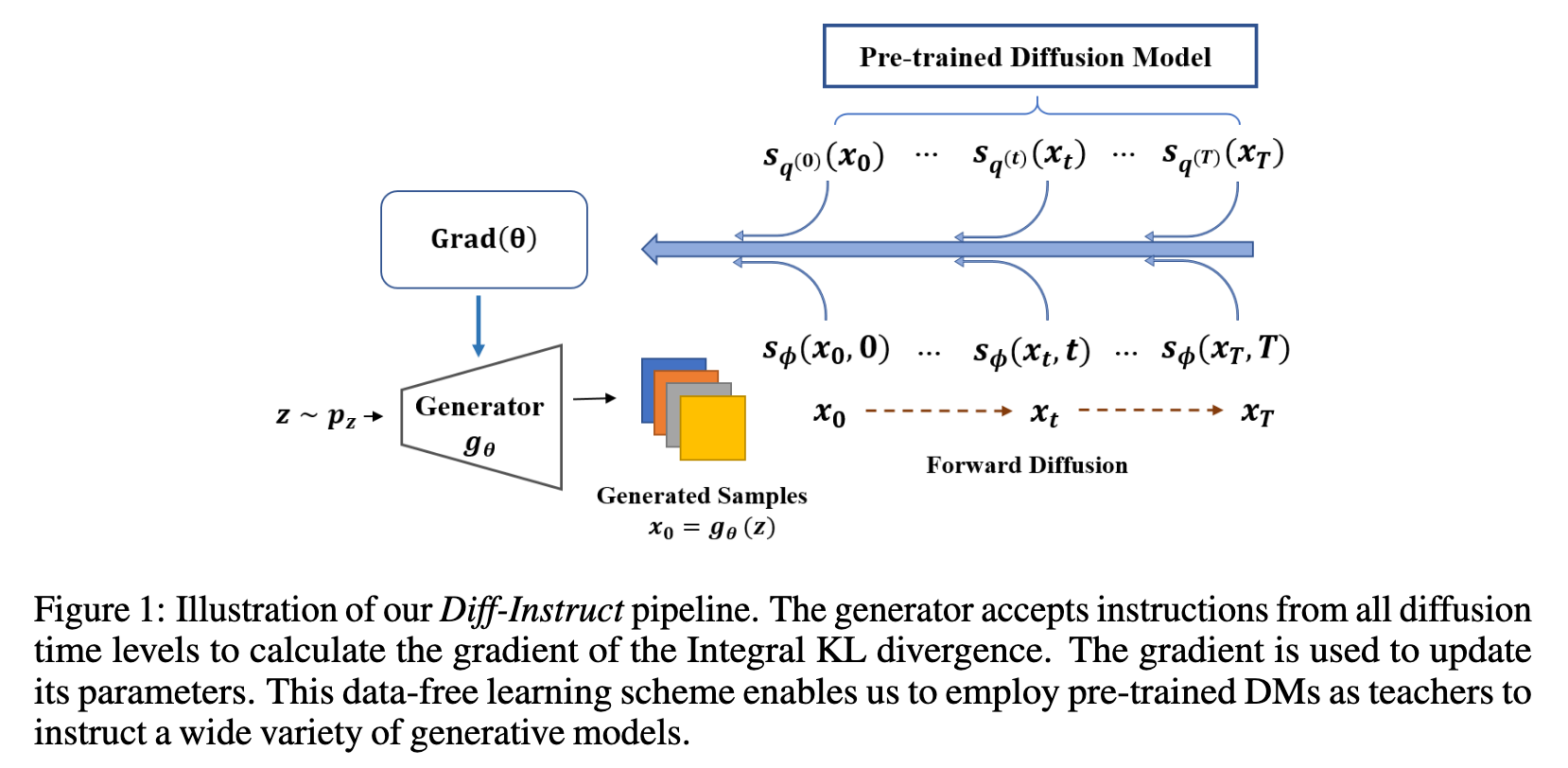
The goal of our Diff-Instruct is to train an implicit model $g_\theta$ without any training data, such that the distribution of the generated samples, denoted as p_g, matches that of the pre-trained DM. (p. 4)
To this end, we consider integrating the Kullback-Leibler divergence along the forward diffusion process with a proper weighting function, such as in (2.2). The resulting Integral Kullback-Leibler (IKL) divergence is a valid probability divergence with two important properties: 1) IKL is more robust than KL in comparing distributions with misaligned supports; 2) The gradient of IKL with respect to the generator’s parameters only requires the marginal score functions of the diffusion process, making it a suitable divergence for incorporating the scoring network of pre-trained diffusion models. (p. 4)
IKL is tailored to incorporate knowledge of pre-trained DMs in multiple time levels. It generalizes the concept of KL divergence to involve all time levels of the diffusion process. (p. 4)
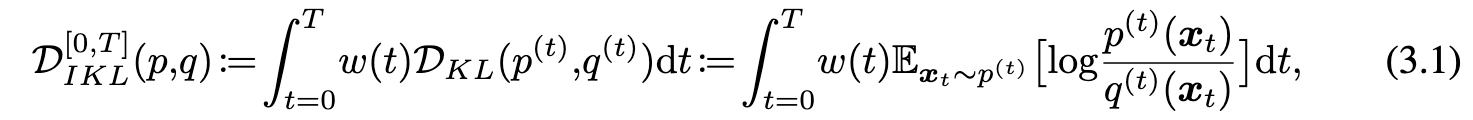
The ILK algorithm could be written as:
Here theta is parameterizes the generator and phi parameterize the learned diffusion model. Note, ILK algorithm alternatives between distilling the new diffusion model (phi) from an existing one (s_q) and updating the generator (theta)
Connections to Existing Methods
Score Distillation Sampling
More precisely, we find that Diff-Instruct’s gradient formula (3.2) will degenerate to the gradient formula of SDS under the assumption that the generator outputs a Dirac distribution. (p. 6)
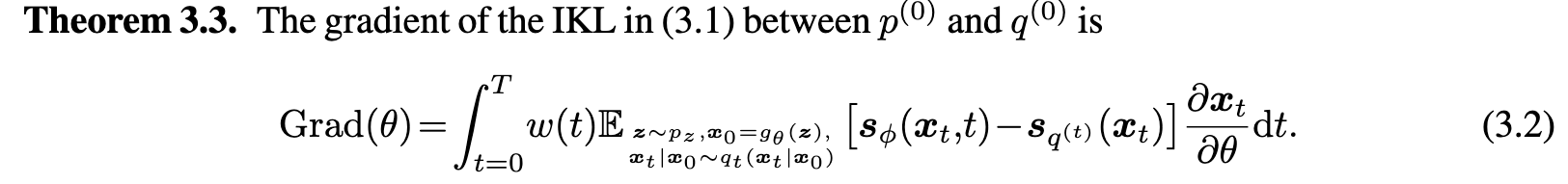
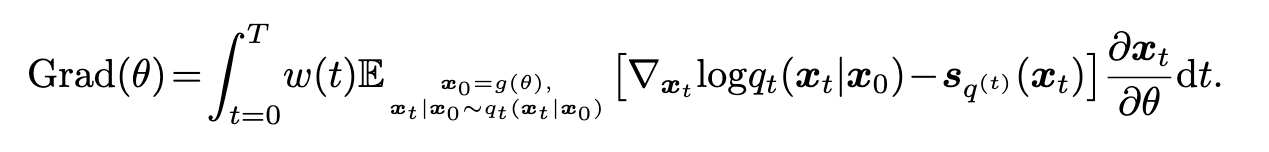
GAN
(3.3) does not depends on another diffusion model s(t) p as in (3.2). So under the assumption of Corollary 3.4, there is no need for using another DM to estimate the generator’s marginal score functions. This is because when the generator outputs a Delta distribution, there is no randomness in x0. (p. 6)
Our proposed Diff-Instruct without integral on time is equivalent to the adversarial training [21] that aims to minimize the KL divergence (p. 6) Corollary 3.5. If the discriminator h learns the perfect density ratio, i.e. h(x) = pd(x) pd(x)+pg(x) , then updating the generator to minimize the KL divergence (L(KL) g in Section 2) is equivalent to Diff-Instruct with a weighting function w(0)= 1 and w(t)= 0,∀t>0. (p. 6)
The Diff-Instruct is essentially a different method from adversarial training in three aspects. First, the adversarial training relies on a discriminator network to learn the density ratio between the model distribution and data distribution. However, Diff-Instruct employs DMs instead of discriminators to instruct the generator updates. Second, in scenarios where only a pre-trained diffusion model is available without any real data samples, Diff-Instruct can distill knowledge from the pre-trained model to the implicit generative model, which is not achievable with adversarial training. Third, Diff-Instruct uses the IKL as the minimization divergence, which overcomes the degeneration problem of the KL divergence via a novel use of diffusion processes and can potentially overcome the drawbacks such as mode-drop issues of adversarial training. (p. 6)
Compared with Existing Work
Experiment Result
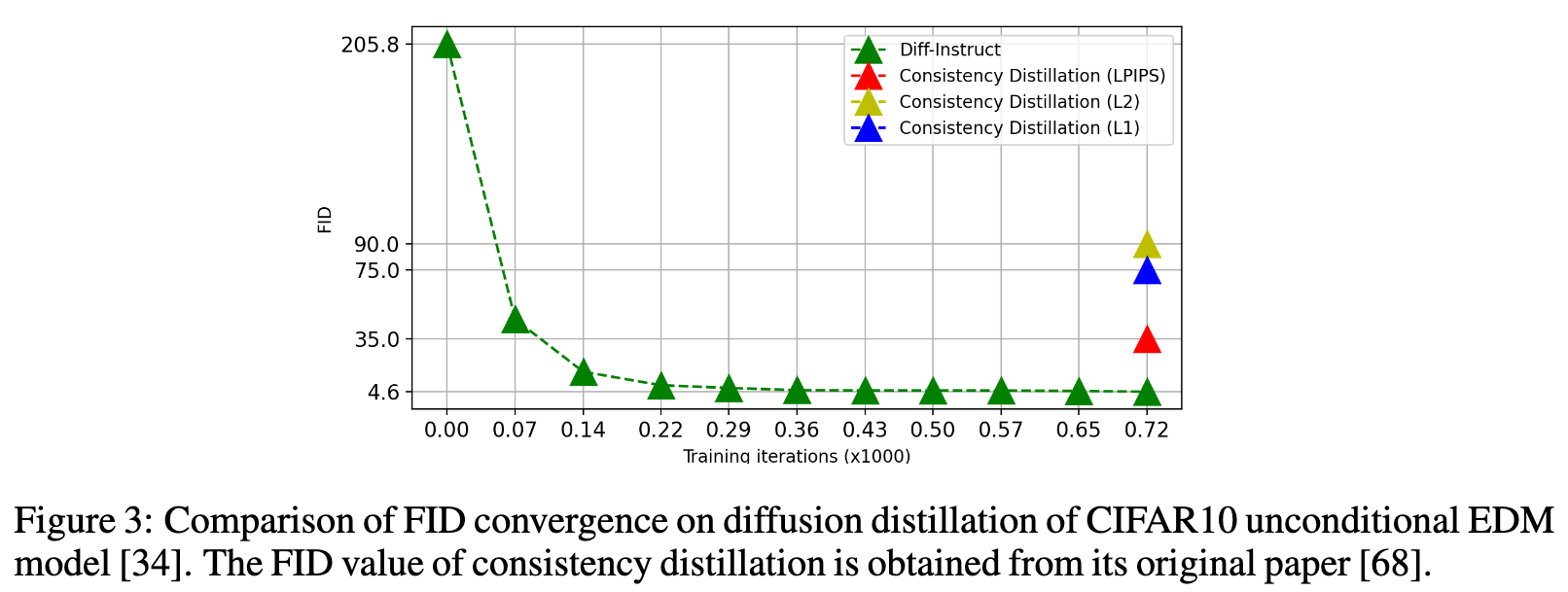
On the unconditional generation of the CIFAR10 dataset, Diff-Instruct achieves the state-of-the-art IS among diffusion-based single-step generative models but achieves the second-best FID, only worse than the consistency distillation (CD) [68] which requires both real data for distillation and the learned neural image metric (e.g. LPIPS [81]). The conditional generation experiment on the CIFAR10 dataset shows that the Diff-Instruct performs better than a 20-NFE diffusion sampling from EDM model [34] with Euler–Maruyama discretization but worse than a 20-NEF Heun discretization.
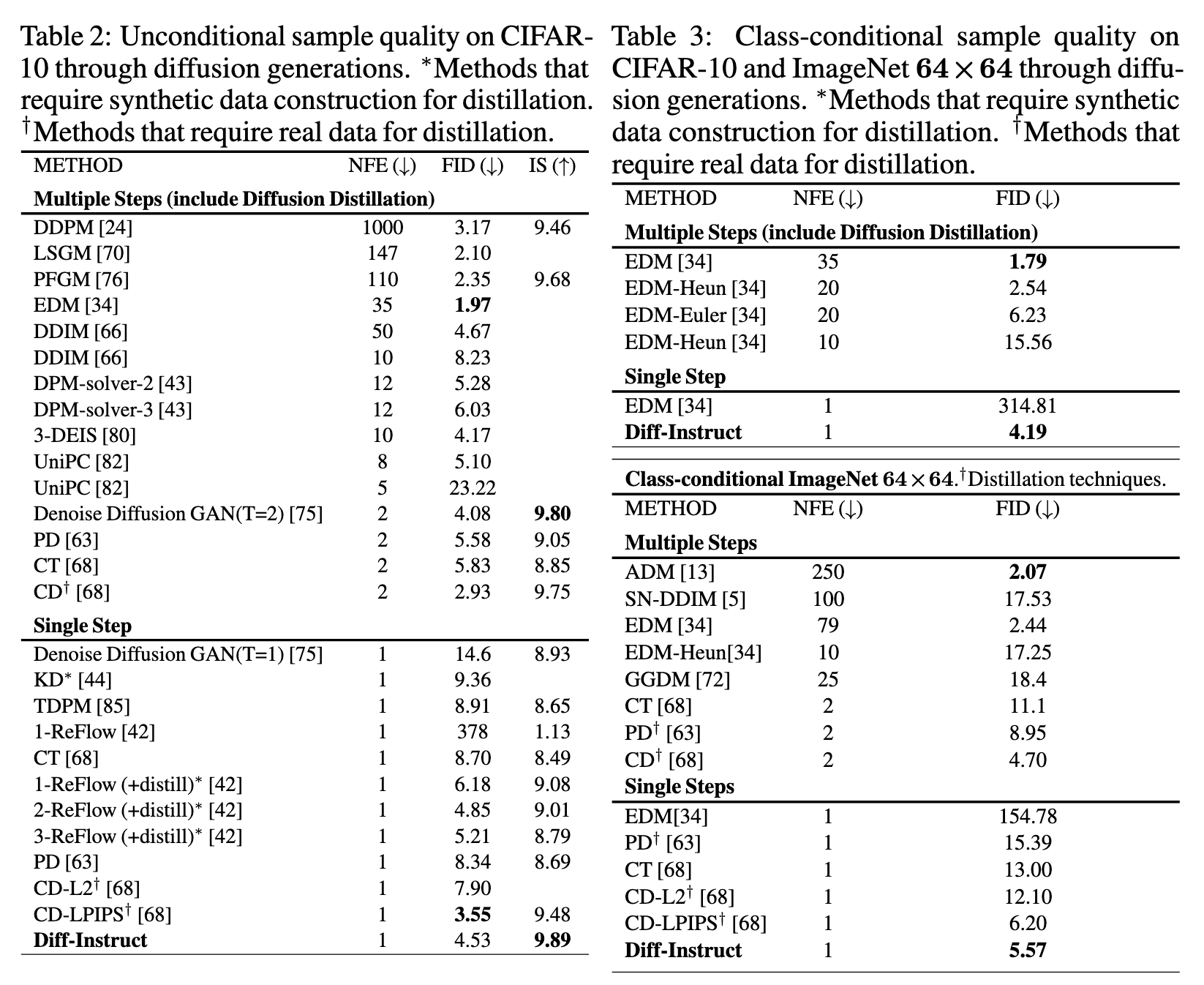
Another advantage of applying Diff-Instruct for diffusion distillation isthe fast convergence speed. We empirically find that Diff-Instruct has a much faster convergence speed than other distillation methods and has a tolerance for a large learning rate for optimization.
