Stable Diffusion

[ diffusion  gan  autoregressor  stable  deep-learning  denoising  ]

This is my 2nd reading note on diffusion model, which will focus on the stabe diffusion, aka High-Resolution Image Synthesis with Latent Diffusion Models. By decomposing the image formation process into a sequential application of denoising autoencoders, diffusion models (DMs) achieve state-of-the-art synthesis results on image data and beyond. However, as mentioned in diffusion, DM sufferes high computational cost. The proposed Latent Diffusion Models (LDM) reduces the computational cost via latent space and introduces cross-attention to enable multi-modality conditioning.

The major contributions of the proposed approaches are:

1. In contrast to purely transformer-based approaches [23, 66], our method scales more graceful to higher dimen- sional data and can thus (a) work on a compression level which provides more faithful and detailed reconstructions than previous work (see Fig. 1) and (b) can be efficiently applied to high-resolution synthesis of megapixel images.
2. We achieve competitive performance on multiple tasks (unconditional image synthesis, inpainting, stochastic super-resolution) and datasets while significantly lowering computational costs. Compared to pixel-based diffusion ap- proaches, we also significantly decrease inference costs.
3. in contrast to previous work [93] which learns both an encoder/decoder architecture and a score-based prior simultaneously, our approach does not re- quire a delicate weighting of reconstruction and generative abilities. This ensures extremely faithful reconstructions and requires very little regularization of the latent space.
4. for densely conditioned tasks such as super-resolution, inpainting and semantic synthesis, our model can be applied in a convolutional fashion and render large, consistent images of ∼ 10242 px.
5. design a general-purpose conditioning mechanism based on cross-attention, enabling multi-modal training. We use it to train class-conditional, text-to-image and layout-to-image models.
6. Finally, we release pretrained latent diffusion and autoencoding models

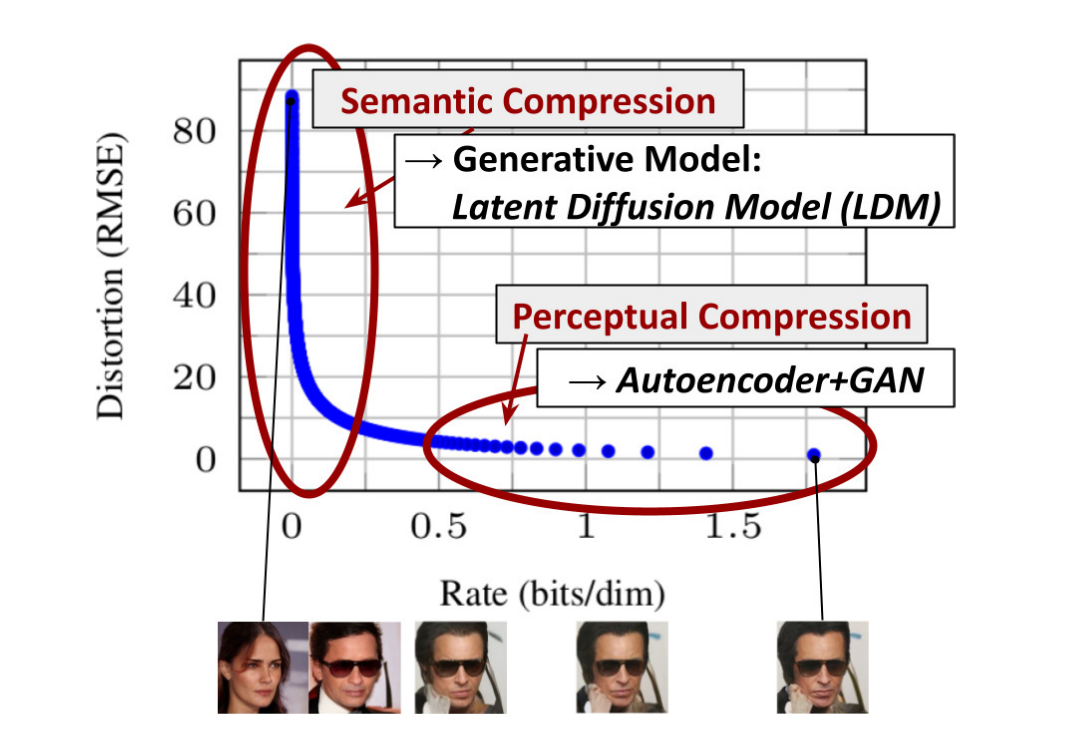
Perceptual Compression vs Semantic Compression

As with any likelihood-based model, learning can be roughly divided into two stages: First is a perceptual compression stage which removes high-frequency details but still learns little semantic variation. In the second stage, the actual generative model learns the semantic and conceptual composition of the data (semantic compression).

We thus aim to first find a perceptually equivalent, but compu- tationally more suitable space, in which we will train diffu- sion models for high-resolution image synthesis.

Reducing Computational Cost via Latent Space

We train an autoencoder which provides a lower-dimensional (and thereby efficient) representational space which is perceptu- ally equivalent to the data space. A notable advantage of this approach is that we need to train the universal autoencoding stage only once and can therefore reuse it for multiple DM trainings or to explore possibly completely different tasks.

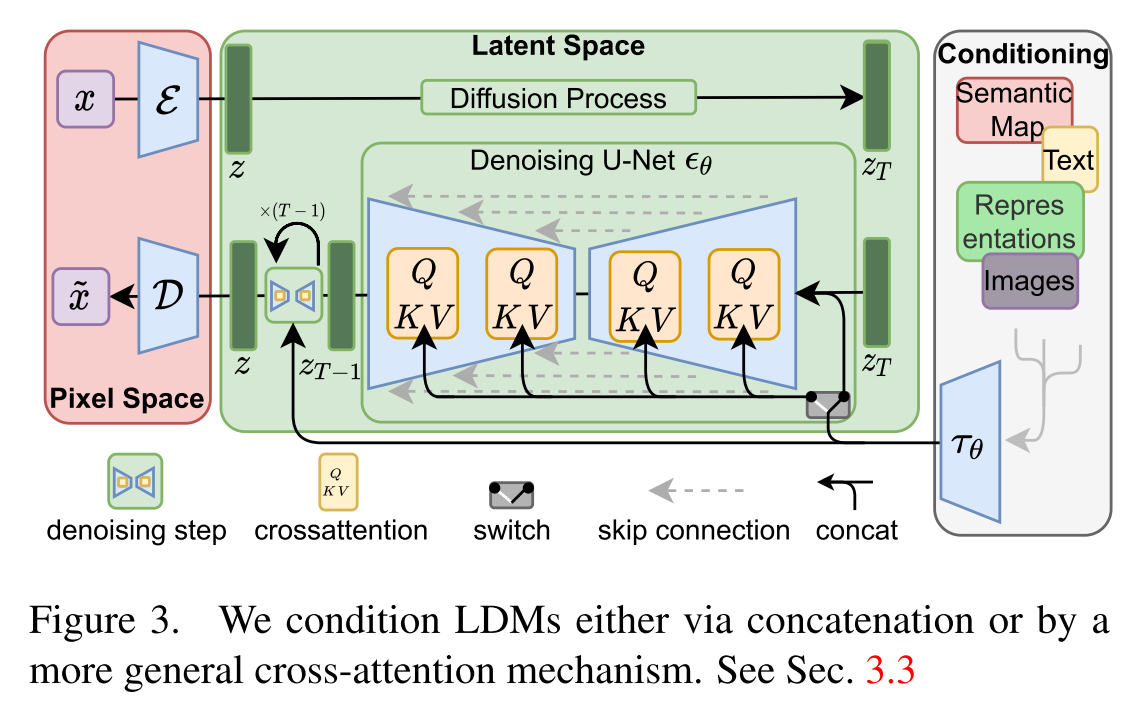
LDM could be illustrated as below. It utilizes encoder \(\mathcal{E}\) to project the input image \(x\in\mathbb{R}^{H\times W\times 3}\) into a latent space \(z\in\mathbb{R}^{h\times w\times c}\). Then z goes through a duffision process and then a denoising process to recover z. The denoising process is a sequence of U-Net, which will be detailed in next section. The latent space is then recovered into image via decoder \(\mathcal{D}\).

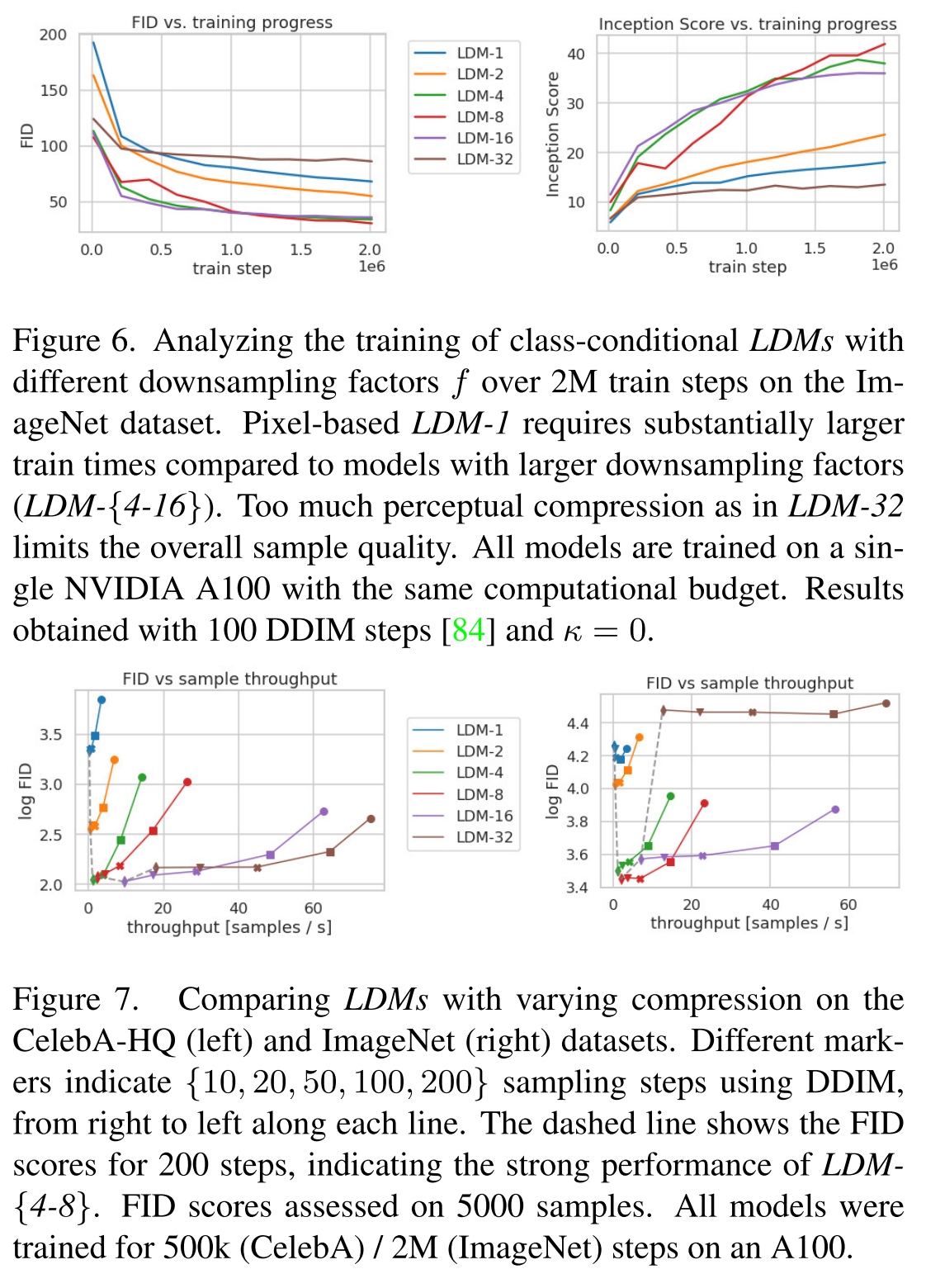
\(f=\frac{H}{h}=\frac{W}{w}\) is the downsamping factor and the paper considers \(f=\{1, 2, 4, 8, 16, 32\}\), where f=1 degrades to vanilla DM.

Our perceptual compression model is based on previous work [23] and consists of an autoencoder trained by com- bination of a perceptual loss [106] and a patch-based [33] adversarial objective [20, 23, 103]. This ensures that the re- constructions are confined to the image manifold by enforcing local realism and avoids bluriness introduced by relying solely on pixel-space losses such as L2 or L1 objectives.

In order to avoid arbitrarily high-variance latent spaces, we experiment with two different kinds of regularizations.

1. KL-reg., imposes a slight KL-penalty towards a standard normal on the learned latent, similar to a VAE [46, 69],
2. VQ-reg. uses a vector quantization layer [96] within the decoder.

Conditioning Mechanisms

LDM also supports other modality input y to condition the denoising process. This can be implemented with a conditional denoising autoencoder \(\theta(z_t, t, y)\) and paves the way to controlling the synthesis process through inputs y such as text [68], semantic maps [33, 61] or other image-to-image translation tasks [34].

We turn DMs into more flexible conditional image generators by augmenting their underlying UNet backbone with the cross-attention mechanism [97], which is effective for learning attention-based models of various input modalities [35,36]. To pre-process y from various modalities (such as language prompts) we introduce a domain specific en- coder τθ that projects y to an intermediate representation \(\tau_\theta(y)\in\mathcal{R}^{M\times d_\tau}\), which is then mapped to the intermediatel ayers of the UNet via a cross-attention layer implementing \(\mbox{Attention}(Q,K, V) = \mbox{softmax}(\frac{QK^T}{\sqrt{d}}\cdot V)\). Here \(\tau_\theta\) is the encoder for the conditioning input.

Experiments

On Perceptual Compression Tradeoffs

For this experiment, the paper compares the computational cost vs image quality score (FID the lower the better, inception score the higher the better) at different f. The results shown below indicate down sampling factor at 4, 8 or 16 is optimal.

Text to Image Synthezation

we train a 1.45B parameter KL-regularized LDM conditioned on language prompts on LAION-400M [78]. We employ the BERT-tokenizer [14] and implement τθ as a transformer [97] to infer a latent code which is mapped into the UNet via (multi-head) cross- attention (Sec. 3.3). This combination of domain specific experts for learning a language representation and visual synthesis results in a powerful model, which generalizes well to complex, user-defined text prompts. The result is shown below.

To further analyze the flexibility of the cross-attention based conditioning mechanism we also train models to synthesize images based on semantic lay- outs on OpenImages [49], and finetune on COCO [4], see Fig. 8. See Sec. D.3 for the quantitative evaluation and im- plementation details.

Image to Image Transfer

By concatenating spatially aligned conditioning informa- tion to the input of θ, LDMs can serve as efficient general-purpose image-to-image translation models. We use this to train models for semantic synthesis, super-resolution (Sec. 4.4) and inpainting (Sec. 4.5). For semantic synthesis, we use images of landscapes paired with semantic maps [23, 61] and concatenate downsampled versions of the se- mantic maps with the latent image representation of a f = 4 model (VQ-reg., see Tab. 8).

We train on an input resolution of 2562 (crops from 3842) but find that our model general- izes to larger resolutions and can generate images up to the megapixel regime when evaluated in a convolutional manner.

Image Superresolution

LDMs can be efficiently trained for super-resolution by diretly conditioning on low-resolution images via concatenation.

Image In-painting

Inpainting is the task of filling masked regions of an image with new content either because parts of the image are are corrupted or to replace existing but undesired content within the image. We evaluate how our general approach for conditional image generation compares to more specialized, state-of-the-art approaches for this task.

For this task, the inpainting mask is used as the conditioning input.

Written on September 23, 2022