Recent Adavances of Diffusion Models
[clip video-diffusion wavegrad diffusion distillation text-image glide deep-learning image-synthesize autoregressive unclip audio-synthesize This is my 4th note in Diffusion models. For the previous notes, please refer to diffusion and stable diffusion. My contents are based on paper listed in Diffusion Explained and Diffusion Models: A Comprehensive Survey of Methods and Applications.
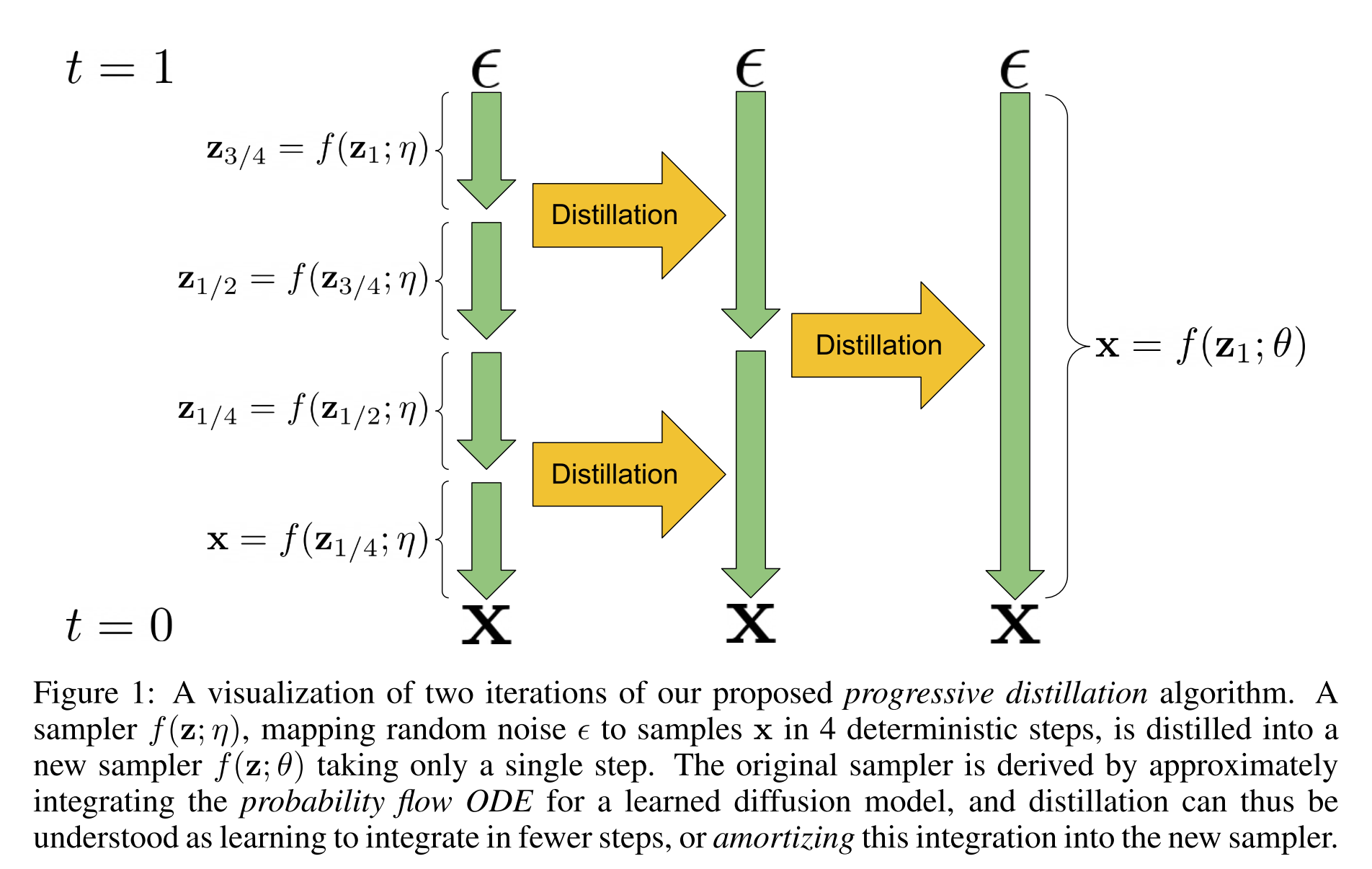
PROGRESSIVE DISTILLATION FOR FAST SAMPLING OF DIFFUSION MODELS
This paper addresses the low sampling speed limitation of diffusion model:
First, we present new parameterizations of diffusion models that provide increased stability when using few sampling steps. Second, we present a method to distill a trained deterministic diffusion sampler, using many steps, into a new diffusion model that takes half as many sampling steps. We then keep progressively applying this distillation proce- dure to our model, halving the number of required sampling steps each time.

Autoregressive Diffusion Models
I didn’t understand this paper!
This paper proposed Autoregressive Diffusion Models (ARDMs), which enables order-agnostic for autoregressive models. This is achived by using a bit-mask to represent the order. This order is sampled at every sampling step.
ARMs model a high-dimensional joint distribution as a factor- ization of conditionals using the probability chain rule. Although very effective, ARMs require a pre-specified order in which to generate data, which may not be an obvious choice for some data modalities, for example images. Further, although the likelihood of ARMs can be retrieved with a single neural network call, sampling from a model requires the same number of network calls as the dimensionality of the data.
Loglikelihood of autoregressive models could be written as below:
Order-agnostic autoregressive models could be written as below, where \(\sigma\) is the sampled order and \(\sigma(\leq t)\) are the indices of element precede \(\sigma(t)\) thus \(\sigma(t)\) depends on \(\sigma(\leq t)\).
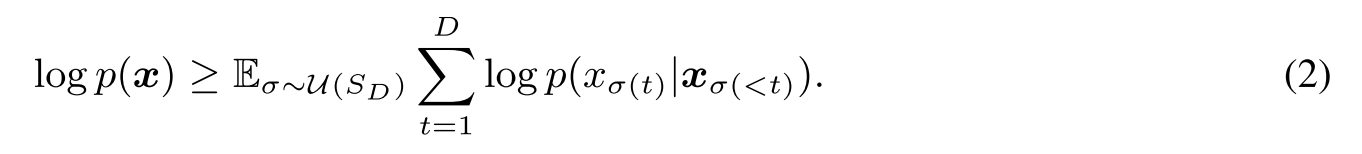
Hierarchical Text-Conditional Image Generation with CLIP Latents
This paper proposes a two-stage model (unCLIP): a prior that generates a CLIP image embedding given a text caption, and a decoder that generates an image conditioned on the image embedding, for generating images from text.
The overview of unCLIP is shown below. The part above is training process which is based on CLIP to train the image encoder and text encoder that aligns to the same space. It requires pairs of text (y) and image (x). The text encoder and image encoder generates the text embedding \(z_t\) and image embedding \(z_i\) accordingly.
| The part below is the inference process, where the prior could be autoregressor or diffusion, and decoder is diffusion model. The process of generating image x from text y could be written as $$p(x | y)=p(x,z_i | y)=p(x | z_i,y)p(z_i | y)$$ |
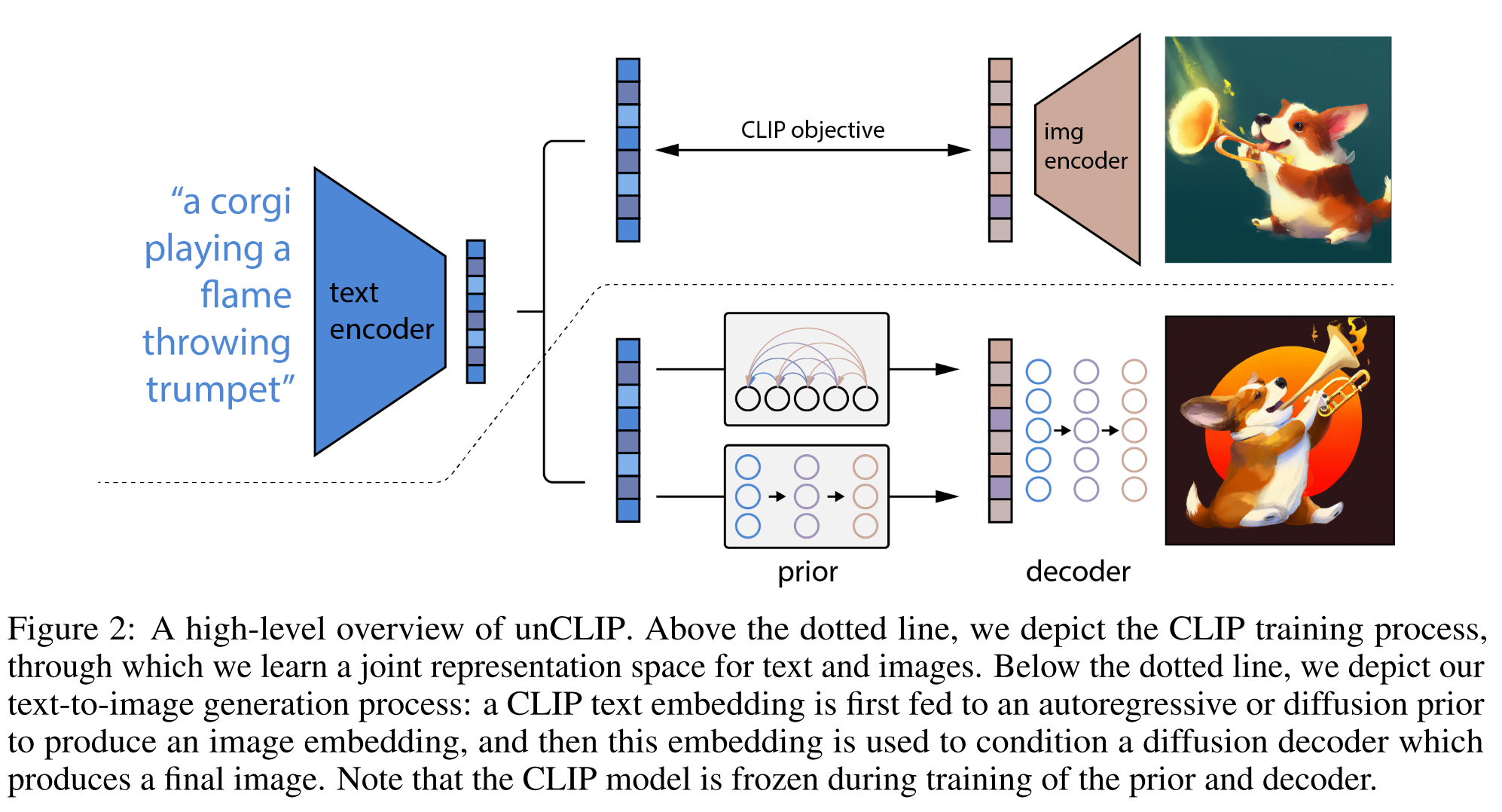
For more information, please check my note in unCLIP.
Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding
The major contribution of this paper is it discover a pre-trained text encoder from large scale text-only corpus could dramatically improves the text-image alignment and visual fidelity of the image generated from text-image generation model. The proposed model is named as Imagen. Imagen contains four components: pre-trained text encoder (T4-XXL is found to be better than CLIP), text-image diffusion model (based on U-Net) and two super resolution models (also based on U-Net).
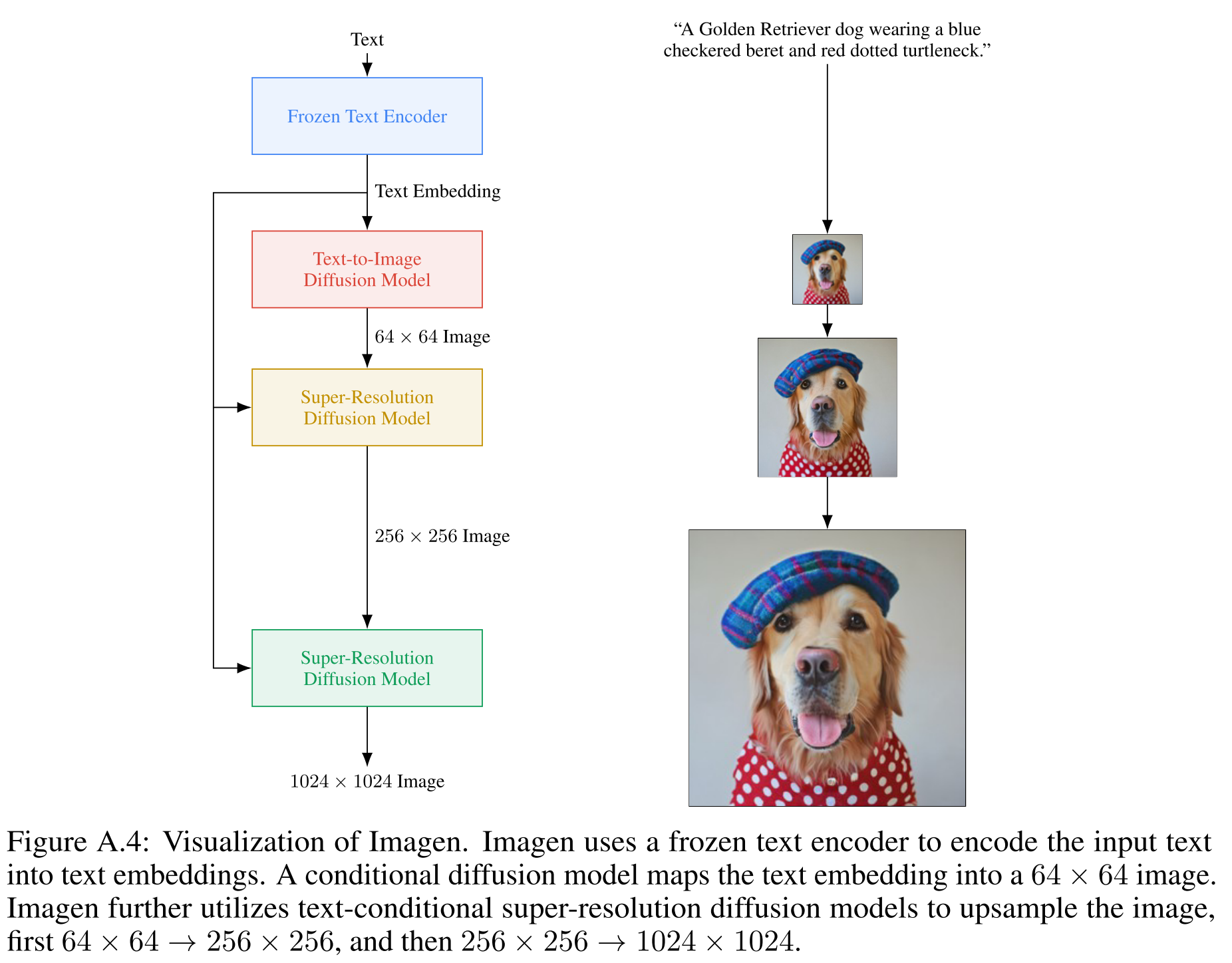
We corroborate the results of recent text-guided diffusion work [16, 41, 54] and find that increasing the classifier-free guidance weight improves image-text alignment, but damages image fidelity producing highly saturated and unnatural images [27]. We find that this is due to a train-test mismatch arising from high guidance weights. To solve this, Imagen proposes dynamic thresholding: at each sampling step we set s to a certain percentile absolute pixel value in \(\hat{x}^t_0\), and if s > 1, then we threshold \(\hat{x}^t_0\) to the range [−s, s] and then divide by s.
Classifier guidance [16] is a technique to improve sample quality while reducing diversity in conditional diffusion models using gradients from a pretrained model $$p(c z_t)$$ during sampling. Classifier-free guidance [27] is an alternative technique that avoids this pretrained model by instead jointly training a single diffusion model on conditional and unconditional objectives via randomly dropping c during training (e.g. with 10% probability).
Video Diffusion Models
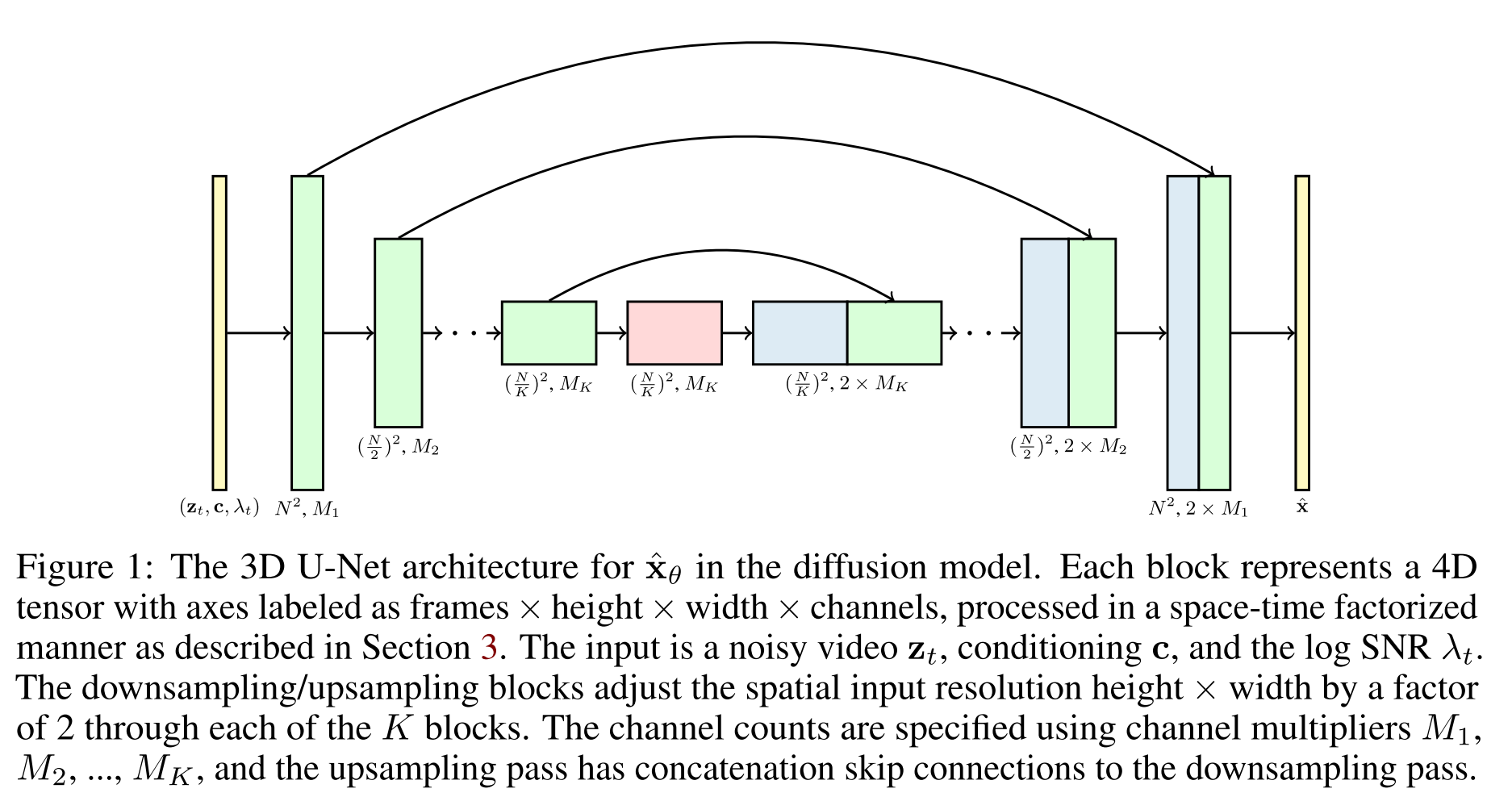
This paper generalizes the image diffusion models to video generation by using a 3D U-Net diffusion model. We train models that generate a fixed number of video frames using a 3D U-Net diffusion model architecture, and we enable generating longer videos by applying this model autoregressively using a new method for conditional generation.
To generate longer videso from from fixed-length video, two methods could be used:
- If xb consists of frames following xa, this allows us to autoregressively extend our sampled videos to arbitrary lengths, which we demonstrate in Section 4.3.3.
- Alternatively, we could choose xa to represent a video of lower frame rate, and then define \(x_b\) to be those frames in between the frames of \(x_a\). This allows one to then to upsample a video temporally, similar to how [34] generate high resolution images through spatial upsampling.
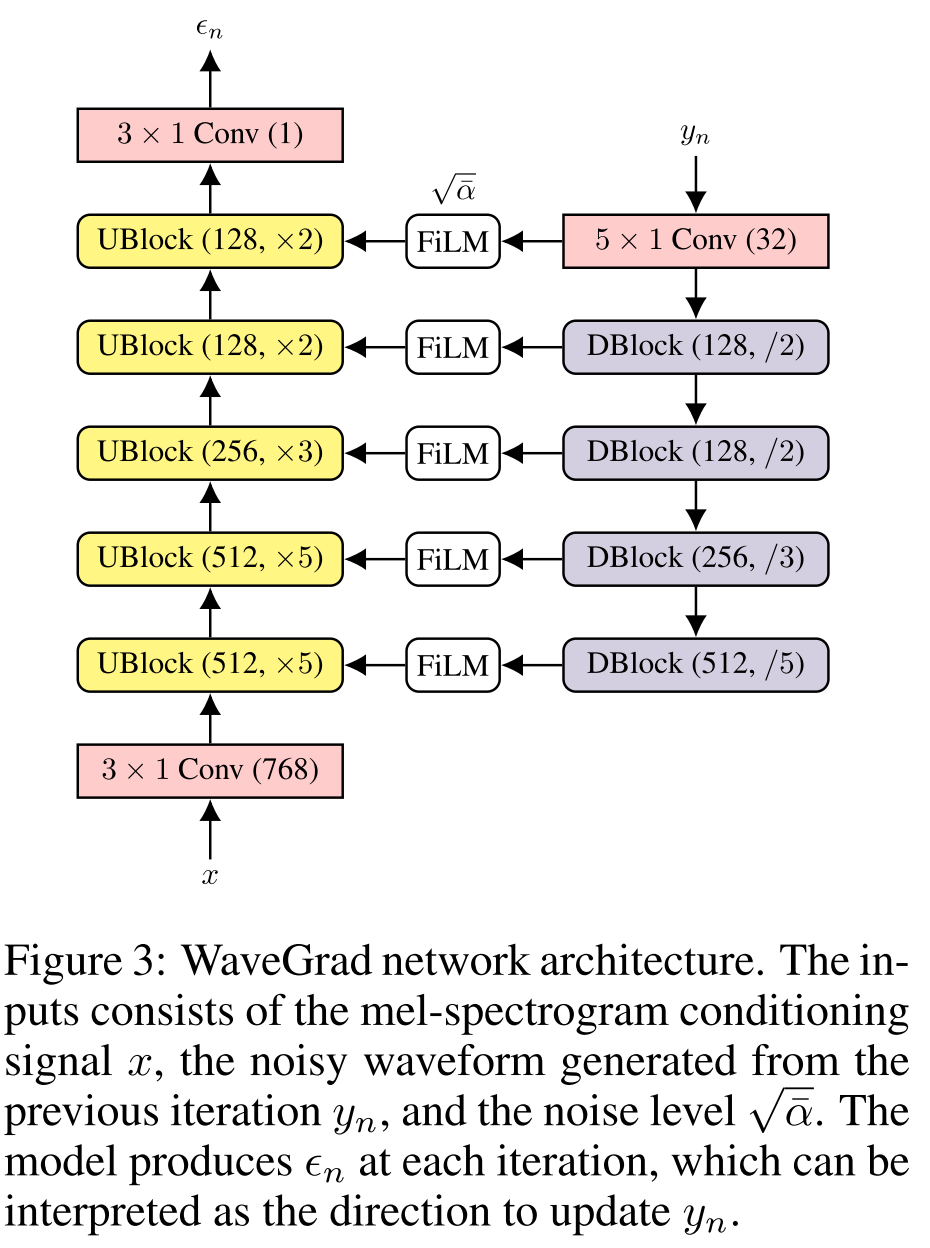
WAVEGRAD: ESTIMATING GRADIENTS FOR WAVEFORM GENERATION
This paper introduces WaveGrad which uses diffusion model to generate high fidelity audio. We find that it can generate high fidelity audio samples using as few as six iterations. The model is still based on 1D U-Net.